|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Természetesen nem az egysejtűről lesz szó, hanem arról a kétszemélyes játékról, amelyhez csak kockás papír és ceruza kell. Ezért nemcsak nálunk terjedt el, hanem az egész világon nagy népszerűségnek örvend. Szokásos szabályai a következők.
A két játékos felváltva egy-egy , illetve jelet tesz a kockás papír mezőibe. Az győz, aki először éri el, hogy legalább szomszédos jele legyen akár vízszintesen, akár függőlegesen, vagy a két átló valamelyikében. Választhatunk más nyerő konfigurációt is. Mint az 1975. évi 6. szám 9. oldalán az 1880. feladattal kapcsolatban beláttuk, ha csak szomszédos jel eléréséig játszunk, a kezdő játékos legkésőbb a hetedik lépésben biztosan nyerhet. Ha a győzelemhez legalább szomszédos jel kell, a játékot NOX-nak nevezzük, ha pontosan jel kell, akkor egzakt NOX-nak.
Az amőbajátéknak sok más variációja is létezik, játszhatunk például úgy is, hogy mindenki megkapja az általa bekerített mezőket (a "bekerítést'' persze definiálni kell), és a végén az győz, aki nagyobb területet hódított meg. Négyzetrács helyett játszhatunk hatszögrácson, vagy a sík (esetleg a tér) valamilyen más rendszerű kitöltésén. Azt is előírhatjuk, hogy egyáltalán hova lehet lépni. Egy időben forgalomban volt a következő társasjáték. Két játékos 32‐32 korongot kap, a korongok egyik oldala kék, a másik piros. Az egyik szín az egyik játékosé, a másik a másiké. A játék az . ábra helyzetéből indul. Csak úgy tehetünk le korongot, ha ezáltal valamelyik egyenes mentén közrefogunk néhány ellenséges korongot, amelyeket átforgatunk a saját színünket mutató oldalukra.
A most is kapható "Logi'' elnevezésű játék is ebbe a családba tartozik (térbeli tic-tac-toe). Két játékos felváltva foglalja el egy térben összeállítható -es kocka mezőit, s az nyer, akinek sikerül négy, egy egyenesen fekvő mezőt elfoglalnia.
1. ábra Visszatérve az eredeti amőba, vagyis az 5 ◯ × játékhoz, annak egyszerűsége lehetővé teszi, hogy a számítógépeket is "megtanítsuk'' játszani. Ehhez olyan programot kell írnunk, amelynek az inputja az amőba tetszőleges helyzete, az output pedig a helyzetnek megfelelő lépés. Egy-egy ilyen program ‐ ha nem is tartozik a legkönnyebb programozói munkák közé ‐ fél év alatt elkészülhet. Eredményül olyan gépet kapunk, amelyik közepesnél jobban amőbázik, nehéz megverni, "sima'' trükköknek nem ugrik be, nem néz el állásokat, és általában jókat lép. Egyáltalán nem kell a programnak bonyolultnak lennie, néhány egyszerű alapelvre épülhet. Azáltal, hogy minden lépésben önállóan döntő programot írunk, bepillantást nyerhetünk más, sokkal bonyolultabb feladatok megoldási módszereibe is. Ugyanezek az alapelvek szolgálnak ugyanis a sakkozóprogramok, sőt a bonyolult döntéseket szolgáló robotok programjainak alapjául. Ezek az utóbbi időben oly sokat emlegetett mesterséges intelligencia fogalomkörébe tartoznak.
Ha emberek játszhatnak amőbát géppel, mi akadálya van annak, hogy gépek játsszanak egymással? Semmi! Sőt, ahogyan világbajnokságon dől el, ki a leggyorsabb futó, ki dobja a súlyt a legmesszebbre, ki a legjobb sakkozó, ugyanígy világbajnokságot írtak ki az amőbázó programoknak is. Ezen Európából 5, Amerikából 13 program indult. Magyarországról a SZTAKI-ban, TPA kisszámítógépre készült program indult.
A kiírásban persze szigorúan rögzítették a játék szabályait: a játékot 19×19-es táblán játsszák. A lépéseket egymással telefonon közlik. A telefonálás idejét is beszámítva, 15 perc alatt mindkét félnek legalább 40 lépést kell tennie. Ha a játszma kétszer 75 lépésben sem fejeződne be, döntetlen az eredmény. Egy fontos eltérés a szokott játéktól: pontosan 5 szomszédos jellel lehet csak nyerni (tehát az egzakt 5 ◯ ×-et játsszák). Végül a programok Európában és Amerikában is körmérkőzést játszanak ‐ mindenki mindenkivel két játszmát ‐, majd a két győztes játszik a világbajnoki címért. A magyar program az európai programok között holtversenyben az 1‐2. helyen végzett, majd az elsőbbségért vívott újabb küzdelemben alulmaradt a későbbi világbajnok dán programmal szemben.
Az idén a SZTAKI matematikusai másik programmal szeretnének indulni. Ezt Mérő László írta az R‐10 számítógépre. Az új program sokkal többet tud elődjénél. Például meg lehet szabni a gép "gondolkodási'' idejét, vagy azt, hogy a gép jól, közepesen vagy éppen gyengén játsszon-e.
Ha végtelen nagy papírunk van, a NOX játékban elvileg három eset lehetséges:
1. a kezdő játékos mindig nyer, azaz van nyerő stratégiája;
2. egyik játékosnak sincs nyerő stratégiája, mindkettő meg tudja akadályozni, hogy a másik nyerjen, azaz akármeddig tudnak játszani anélkül, hogy bármelyik is nyerne; végül
3. a második játékosnak van nyerő stratégiája.
Megmutatjuk, hogy a nem egzakt NOX esetén a 3. eset nem lehetséges. Tegyük fel, hogy mégis van a másodiknak nyerő stratégiája, azaz van olyan utasításrendszer, amit ha a második játékos betart, biztosan nyer. Ekkor az első játékos a következőképpen játszhat. Elsőre lépjen valamit, mindegy hogy mit. Azután játsszon úgy, mintha ő lenne a második játékos. Ha a stratégia szerint valahová tennie kell, elképzelhető, hogy az a hely foglalt: éppen ő foglalta le az első lépésével. De ez nem baj, hiszen mindegy, mikor tette meg ezt a lépést. Sőt van még egy felesleges lépése is, ezzel ismét tetszőleges négyzetbe tehet. S ezzel éppen a második stratégiája biztosítja az elsőnek a győzelmet, ami ellentmond annak, hogy a második győzhet.
Így csak az 1. és 2. eset lehetséges, azaz a kezdő játékos (ha játék közben nem hibázik) nem veszthet! A másodiknak legfeljebb arra van esélye, hogy vereségét elodázza.
 2. ábra
A bizonyítás teljességéhez előbb tisztázni kellett volna, mit is értünk "stratégián''. A kezdő játékos stratégiája egy utasítássorozat: az első lépését melyik mezőre tegye; azután a második játékos összes lehetséges első lépésére mondja meg, mi a kezdő második lépése; a másik erre adható összes válaszára mondja meg a kezdő 3. lépését stb. A stratégia ‐ többek között ‐ fa-gráffal is ábrázolható (2. ábra). A gráf minden csúcsa egy-egy mezőt jelent. A legfelső, K1 jelű sorban levő egyetlen csúcsa az első játékos kezdő lépését jelzi. A következő, M1 sorban a második játékos minden lehetséges válaszlépése, a harmadik, K2 sorban az elsőnek ezekre adandó válaszai találhatók stb. Egy-egy játék lefolyását tehát mindig egy felülről lefelé haladó élsorozat mutatja. (Ezeket láncoknak nevezik, ábránkon egyet megvastagítottunk.) Az élsorozat akkor ér véget, ha az utolsó lépéssel vagy a kezdő, vagy a másik játékos egy nyerő konfigurációt állított elő. Egy ilyen gráffal ábrázolt stratégia az első játékosnak nyerő, ha minden lánc páratlan sorszámú sorban (emeleten) ér véget; és döntetlen, ha a láncvégek páratlan sorszámú sorokban vannak, de vannak láncok, melyek nem érnek véget. (Ezek jelzik az akármeddig tartó játékot.)
Igazolható, hogy ha a NOX játékban a kezdőnek van nyerő stratégiája, akkor a fának csak véges sok sora lehet. (Ez még nem következik abból, hogy minden lánc véget ér valahol!) Másrészt minden páratlan sorban álló csúcs végtelen sokfelé ágazik szét (a második lehetséges lépéseinek megfelelően), ezért az sem nyilvánvaló, bár jelen esetben igaz, hogy a stratégiát valamilyen véges leírással is meg lehet adni, azaz lehet a stratégia szerint játszó programot írni. Elképzelhető ugyanis, hogy a stratégia létezik, de nem lehet (elvileg nem lehet és nem azért, mert ügyetlenek vagyunk) a stratégia szerint játszó programot írni.
Sajnos, a fenti bizonyítás nem alkalmazható a világbajnokságon kiírt játékra (éppen amiatt a kikötés miatt, hogy pontosan 5 szomszédos jellel lehet csak nyerni), Így elképzelhető, hogy ebben az esetben a második játékosnak van nyerő stratégiája. Említettük már, hogy a nem egzakt NOX játékban az N=4 esetben a kezdő játékos nyerni tud. Ha N=5, akkor nem tudjuk, mi a helyzet, van-e nyerő stratégiája a kezdőnek vagy sem. Azt mindenesetre tudjuk, hogy van olyan stratégiája, amit játszva, nem kap ki, de ‐ sajnos vagy szerencsére ‐ ilyen stratégiát nem ismerünk. Mivel a játszmák 80‐90 százalékát a kezdő nyeri, valószínűnek látszik, hogy a kezdőnek van nyerő stratégiája.
Mi a helyzet N nagyobb értékeinél? Ha valamilyen N=N0-ra van a másodiknak döntetlen stratégiája (vagyis amivel meg tudja akadályozni, hogy az első nyerjen), akkor ezt játszva az első nem tud sem N0, sem annál hosszabb "láncot'' készíteni. Így ez a stratégia minden N≧N0-ra is döntetlen stratégia a második játékosnak. De van-e, akármekkora N-re is, a második játékosnak döntetlen stratégiája?
A válasz igen. A következő, Nagy Zsigmondtól származó stratégiát követve az első játékos legfeljebb 11 hosszúságú láncokat tud készíteni, azaz N=12-re a másodiknak van döntetlen stratégiája.
 3. ábra
 4. ábra
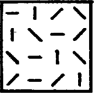
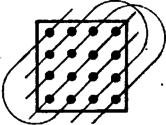
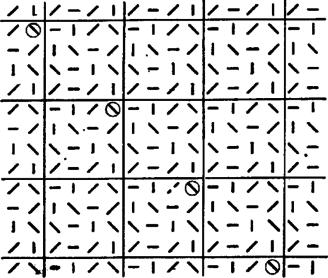
Osszuk fel a játékteret 4×4-es négyzetekre és mindegyikbe helyezzük el a 3.ábrán látható mintát. Ezzel az 5. ábra szerinti kitöltést kapjuk. Figyelmesen megnézve a 3. ábrát észrevehetjük, hogy minden oszlopban van függőleges vonal, minden sorban vízszintes vonal, minden, a 4. ábrán látható tört átlóban egy / vonal, és minden másik irányú tört átlóban egy \ vonal. Nevezzünk két mezőt "szomszédos''-nak, ha bennük egyforma jelek vannak, és egymástól a jelek irányában pontosan 4 mezőnyire vannak. Ily módon minden mezőnek pontosan két ,,szomszéd''-ja van, mindkét irányban egy-egy. (Az 5. ábrán négy "szomszédos'' mezőt megjelöltünk.) A "szomszédos'' mezők úgy helyezkednek el, mint egy végtelen hosszú cérnán egyenlő távolságra kötött gyöngyszemek.
 5. ábra
Helyezzünk most el tetszőleges, legalább 12 hosszúságú láncot a játéktérre. A kitöltés előbb megfigyelt szabályszerűsége miatt a láncban legalább három olyan mező van, ami a lánc irányába mutató vonalakat tartalmaz, azaz tartalmaz három "szomszédos'' mezőt. Így elég, ha a második el tudja érni, hogy az első ne foglaljon el három "szomszédos'' mezőt Ezt viszont nagyon könnyen megteheti. Ha az első akármelyik mezőre is tesz, annak két "szomszéd''-ja közül valamelyikre kell tennie, mégpedig úgy, hogy a "szomszédos'' mezőkön felváltva ◯ és × legyen. (Persze éppen a stratégia biztosítja, hogy ezt mindig meg lehet tenni.)
 6. ábra
A továbbiakban egy másik stratégiát ismertetünk vázlatosan, amellyel a második játékos már N=9 mellett is döntetlent érhet el. Ehhez először egy másik játékkal ismerkedünk meg.
Ketten felváltva egy 5×5 méretű tábla mezőit foglalják el. A kezdő játékos nyer, ha vagy egy teljes sort, egy teljes oszlopot vagy a 6. ábrán látható, 3, 4 vagy 5 mezőből álló átlók valamelyikét sikerül lefoglalnia. Néhány játszma után láthatjuk, hogy a második játékos mindig megakadályozhatja az elsőt a győzelemben. Arra kell csak ügyelnie, hogy elsőként a 7. ábrán 1-essel vagy 2-essel jelölt mezőket foglalja el. (A teljes stratégia leírása több száz oldalt tenne ki!)
7. ábra
Osszuk fel az amőba játékmezőjét 5×5-ös kis négyzetekre. A második játékos minden ilyen kis négyzetben külön-külön játszik, mégpedig nem amőbát, hanem a most ismertetett játékot. Azt, hogy egy-egy lépéspárt melyik négyzetbe teszik, az első dönti el: amelyikbe ő tesz, abba tesz a második játékos is. (Ha már nincs hely, akkor oda tesz, ahová akar.)
A kezdő játékosnak nem lehet kilenc szomszédos jele, mert ha volna, akkor valamelyik kis 5×5-ös négyzetnek egy teljes sorát, teljes oszlopát vagy valamelyik, a 6. ábrán látható átlóját is lefoglalta volna.
A hiányzó N=5, 6, 7, 8 esetekről nem tudunk semmit. Valószínű, hogy N=5-re még a kezdő játékosnak van nyerő stratégiája, csak az 30‐50 lépéses. Nem hiszem, hogy ezt valaha meg fogják találni.
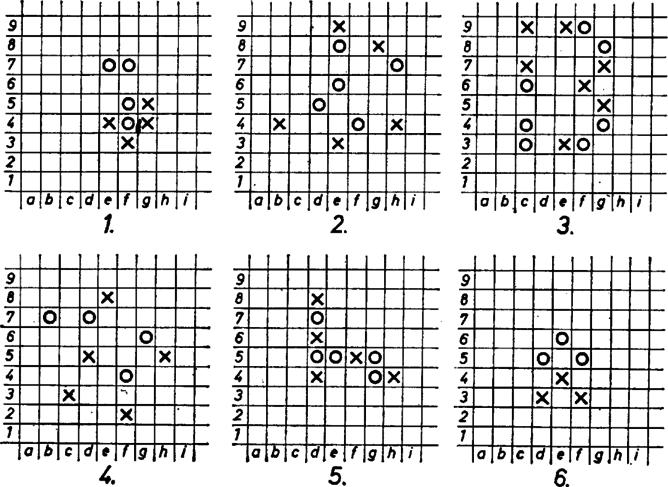 8. ábra
Végül bemutatunk néhány érdekes amőba végjátékot, melyeket Oláh Zsolt szegedi olvasónk küldött be. A rejtvények mindegyikében ◯ (karika) indul és 4, 5, 6 vagy 8 lépésben nyer. A mezőkben levő betűk és számok csak a megoldás leírására szolgálnak, a játékmezőt végtelen nagynak gondoljuk. Jó szórakozást kívánunk! (A megoldásokat a 209. oldalon közöljük.) |
 PDF | MathML
PDF | MathML 




