Kezdőlap


Cím:	Egy érdekes és egyszerű geometriai transzformációval származtatott affin sík
Szerző(k):	Kárteszi Ferenc
Füzet:	1978/november, 97 - 103. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feladatmegoldásban ügyes tanulók felkészültségének és képességének felmérésére először húsz évvel ezelőtt, és azóta is többször kitűztem azt a feladatot, amelyről ez a cikk szól. Nemcsak versenyre készülő középiskolásokat, hanem egyetemi hallgatókat is próbára tettem vele. Egyszer sem kaptam meg azt, amit vártam; általában hosszadalmas és nehézkes megoldásokat adtak még azok is, akik máskor kitűntek ötletességükkel. Éppen ezért úgy vélem, hogy a szükséges előismeretek, az egyszerű megoldás közlése, az alkalmazott módszer elemzése tanulságos lehet azok számára is, akik már sikeresen szerepeltek versenyeken.

A probléma. ‐ Az euklideszi síkból egy jól meghatározott, új "sík"-nak nevezett alakzatot származtatunk.
Az euklideszi sík pontjait az új "sík"-on is pontoknak tekintjük. Az "egyenesek'' szerepét azonban az euklideszi sík bizonyos parabolái és egyenesei játsszák. Olyan ez a "sík'', mint az euklideszi sík görbe tükörben mutatkozó képe; némelyik egyenes képe elgörbül. Most részletezzük, hogy az új "sík"-on mi játssza az "egyenes'' szerepét.

A síkbeli mozgások közül az eltolásra vonatkozó tudnivalók a következők:
A sík önmagában való minden eltolásához egy-egy vektor, eltolásvektor tartozik. A sík minden pontjának kezdőhelyzete és eltolás utáni véghelyzete ugyanazt a vektort szolgáltatja, ez a szóban forgó eltolás eltolásvektora. A sík önmagában való eltolásai, mint elemek, egy halmazt alkotnak, ezt a halmazt

Θ

-val fogjuk jelölni, egy-egy elemét görög kisbetűvel (például

τ \in Θ

). A sík egy rögzített pontja legyen az

O

. A sík

O

kezdőpontú vektorai, mint elemek, egy

T

halmazt alkotnak. Ennek elemeit latin kisbetűkkel jelöljük (például

t \in T

). A mondottak szerint

Θ

és

T

közt egy-egyértelmű megfeleltetés (bijekció) áll fenn, amit hiba volna azonosságnak tekinteni.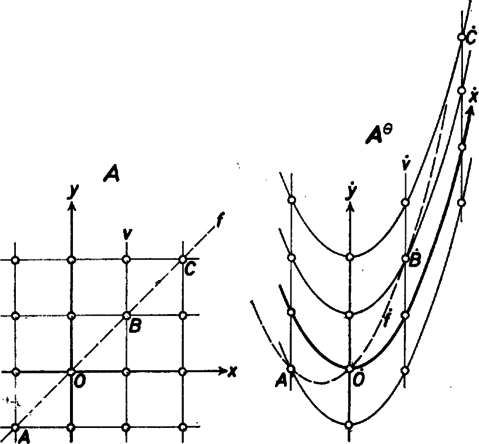

1. ábra

Legyen az euklideszi sík egy rögzített parabolája

p

, annak szimmetriatengelye az

y

egyenes. Egy

τ

eltolás vigye át a parabolát a

p^{τ}

parabolába, az

y

egyenest a vele párhuzamos

y^{τ}

egyenesbe.
Az új "sík"-on az "egyenesek"-et az ily módon származtatott

p^{τ}

és

y^{τ}

vonalak képviselik; míg a

τ

végigfut a

Θ

összes elemein, előállnak a "sík'' "egyenesei''. Ezért fogjuk a

Σ

euklideszi síkból így származtatott síkot

Σ^{Θ}

-val jelölni. A

Σ

és

Σ^{Θ}

közti viszonyt az

1.

ábra

A

és

A^{Θ}

része közti viszony érzékelteti.
Az euklideszi A ábrának az

A^{Θ}

ábra egy torzképe: mert bizonyos euklideszi viszonyok némelyikét a tükörkép eltorzítja. Például az

A

ábra

A

O

B

C

pontjai az

f

egyenesen vannak, az

A^{Θ}

ábrán az

\dot{A}

\dot{O}

\dot{B}

\dot{C}

képpontok ugyancsak az

\dot{f}

képegyenesen helyezkednek el. Ugyanakkor a

v

egyenes merőleges az

x

egyenesre, de a

\dot{v}

képvonal nem merőleges az

\dot{x}

képvonalra. Vagyis a kép az illeszkedést tükrözi, de a merőlegességet elrontja.
Most már megfogalmazhatjuk a bevezetésben említett feladatot:

1.

Bizonyítandó, hogy a

Σ^{Θ}

egy affin sík.

2.

Eldöntendő, hogy ezen az affin síkon érvényes-e a háromszögpárra vonatkozó Desargues-tétel.

A szükséges előismeretek. Először L. Euler

(1707 - 1783)

kezdte vizsgálni más tulajdonságoktól elkülönítve az euklideszi sík olyan tulajdonságait, amelyek síknak síkra való párhuzamos vetítésével a vetületre is átöröklődnek. Ő nevezte el az ilyen tulajdonságokat affin tulajdonságoknak. Másfél évszázad múlva megújult a téma iránti érdeklődés (aminek egyik oka bizonyos fizikai problémák tisztázására törekvő kutatómunka volt); igyekeztek olyan egyszerű, de kellőképpen erős axiómarendszert találni, amelyből az affin sík tulajdonságait kifejező minden lényeges tétel levezethető. Így bontakozott ki az affin sík (affin geometria) mai fogalma.
Az affin sík egy nem üres ponthalmaz, amelyet bizonyos (egyeneseknek nevezett) részhalmazai által geometriai alakzattá szervezünk, mégpedig úgy, hogy teljesüljenek a következő axiómák:

A_{1}

: A sík tetszőlegesen adott két (különböző) pontját egyaránt tartalmazó egyenes létezik, és csak egy ilyen egyenes van.

A_{2}

: Egy tetszőlegesen adott pontot tartalmazó egyenesek halmazában egyetlenegy olyan egyenes van, amely e pontot nem tartalmazó, különben tetszőleges egyenesnek semelyik pontját sem tartalmazza.

A_{3}

: Van olyan három pont, hogy azok mindegyikét semelyik egyenes sem tartalmazza.
Ezekre az axiómákra röviden az összekötés, a párhuzamosság, a háromszög axiómája néven utalunk. Ezek az axiómák az euklideszi sík néhány szemléletesen nyilvánvaló tulajdonságát fejezik ki a halmazok elvont nyelvén. Ezért világos, hogy e három axiómából álló axiómarendszer nem "üres'' definíció, de majd meglátjuk, hogy nemcsak az euklideszi síkot jellemzi. Affin sík minden olyan szervezett ponthalmaz, amelyre nézve ez az axiómarendszer teljesül.
A Descartes-féle koordináta-geometria módszere lehetővé tette az euklideszi geometria leírását algebrai módszerekkel. Hajlékony eszközzé vált a geometriai problémák megoldásában. Természetesnek látszik az a törekvés, hogy az

A_{1}

A_{2}

A_{3}

axiómákkal definiált síkon is valami hasonló módszert találjunk. Tudjuk azonban, hogy a Descartes-féle koordinátafogalom az euklideszi geometria olyan fogalmaira épül (például a távolság és a merőlegesség), amelyeknek az affin síkon nincs értelme. Mégis sikerült a koordinátafogalmat úgy általánosítani, hogy az már az affin síkon is értelmezhető, vagyis az euklideszi metrikától független. Ebben az új fogalomalkotásban döntő szerephez jut G. Desargues

(1593 - 1662)

egy régen ismert tétele. Ez a tétel az affin síkra nézve a következőképpen fogalmazható:
Legyen a sík hat, páronként különböző pontja

A

B

C

;

\dot{A}

\dot{B}

\dot{C}

, mégpedig olyan helyzetben, hogy se az első három, se az utolsó három ne essék egy egyenesbe. Ezekre vonatkozik a szóban forgó (röviden)

D

-tétel:
Az

A \dot{A}

B \dot{B}

C \dot{C}

egyenesek akkor és csak akkor találkoznak egy pontban, vagy párhuzamosak, ha
(i) az

A B \cap \dot{A} \dot{B} = \ddot{C}

B C \cap \dot{B} \dot{C} = Ä

C A \cap \dot{C} \dot{A} = \ddot{B}

metszéspontok egy egyenesen vannak; vagy
(ii) a három egyenespár közül az egyiknek az egyenesei párhuzamosak a másik kettővel meghatározott metszéspontokat összekötő egyenessel; vagy
(iii) mind a három párt párhuzamos egyenesek alkotják, vagyis

A B ∥ \dot{A} \dot{B}

B C ∥ \dot{B} \dot{C}

C A ∥ \dot{C} \dot{A}

.
D. Hilbert

(1862 - 1943)

észrevette és bebizonyította, hogy az új koordinátaforgalom a

D

-tétel egy gyöngébb változatára is felépíthető. Ezt a tételt

D^{*}

-gal jelöljük:
Ha az

A B C

és

\dot{A} \dot{B} \dot{C}

háromszög helyzete olyan, hogy az

A \dot{A}

B \dot{B}

C \dot{C}

egyenesek egy

S

pontban találkoznak, vagy párhuzamosak, továbbá ha

A B ∥ \dot{A} \dot{B}

és

A C ∥ \dot{A} \dot{C}

, akkor

B C ∥ \dot{B} \dot{C}

(Ezt szemlélteti a

2.

ábra jobb és bal oldali képe.)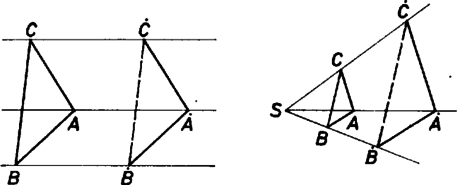

2. ábra

Ebből a gyönge

D^{*}

-tételből a

D

-tétel levezethető. Felvetődik a kérdés, hogy az affin síkot definiáló axiómarendszerből levezethető-e a

D^{*}

-tétel. Hilbert bebizonyította, hogy nem vezethető le, mert van olyan affin sík, amelyen a

D^{*}

-tétel nem érvényes. Később Hilbert bizonyítását többen is egyszerűsítették, és F. R. Moulton

1902

-ben egy zseniálisan egyszerű bizonyítást közölt.
Érthető, hogy ezek után további axiómával bővítették az affin síkot definiáló axiómarendszert, avégett, hogy a síkon a koordináták bevezetése lehetővé váljék. Ez a további axióma a következő:

A_{4}

: A síkon érvényes a

D^{*}

-tétel.
Az

A_{1}

A_{2}

A_{3}

A_{4}

axiómarendszerrel definiált speciális affin síkot Desargues-féle affin síknak nevezzük.
A geometria tanításának középiskolai programjában szerepel ugyan a geometriai transzformációkat alkalmazó gondolkodásmód kialakítása és fejlesztése, azonban az e célra szolgáló ismeretanyag nagyon szegény, a gondolkodás fejlesztésére szánt témák alacsony színvonalúak és érdektelenek. Még a lineáris transzformációk közül is csak a legspeciálisabbak szerepelnek, sőt azok is csak hiányos, széteső feldolgozásban.
A transzformációra támaszkodó gondolkodásmód erejének érzékeltetése céljára a következőkben egy egyszerű, nemlineáris transzformációt ismertetünk.
Legyen az euklideszi síkon egy rögzített Descartes-féle koordináta-rendszerünk. Arra vonatkoztatva tekintsünk egy

(x, y)

tárgypontot és egy

ϱ

transzformáció szerint e ponthoz rendelt

(\dot{x}, \dot{y})

képpontot. Most a

ϱ

transzformációt a

\begin{matrix} \dot{x} & = x, & (1) \\ \dot{y} & = x^{2} + y \end{matrix}

utasítással definiáljuk. Az

(1)

-ből világos, hogy a sík minden pontjának van képe, mégpedig egy pontnak egy képe van. Az

(1)

-ből könnyen következik

\begin{matrix} x & = \dot{x}, & (2) \\ y & = - {\dot{x}}^{2} + \dot{y}, \end{matrix}

amiből pedig az világos, hogy a sík bármely

(\dot{x}, \dot{y})

pontja képpontnak tekinthető, mert van őse, mégpedig egy, az

(x, y)

tárgypont. Az ilyen tulajdonságú transzformációt bijektívnek mondjuk.
Most egy látszólag hasonló példát tekintünk, az

\begin{matrix} {\dot{x}}^{2} & = x^{2} + y^{2}, & (3) \\ \dot{y} & = x y \end{matrix}

utasítással definiált

σ

transzformációt. Ez egyrészt olyan, mint a

ϱ

, mert

σ

szerint is az euklideszi sík minden pontjának van képe, mégpedig egy pontnak egy képe van. Másrészt azonban nem olyan, mert nem igaz, hogy minden pont képpontnak tekinthető. Például a

(- 1, - 1)

pont semelyik pontnak sem képe. Az sem igaz, hogy ha egy pontnak van őse, akkor csak egy őse van. Például a

(25, 12)

pontnak

4

őse van:

(3, 4)

(4, 3)

(- 3, - 4)

(- 4, - 3)

. A

σ

tehát nem bijektív transzformáció.
A

ϱ

és

σ

transzformáció közti különbség ‐ vagyis az, hogy a

ϱ

egy-egyértelmű, míg a

σ

csupán egyértelmű ‐ abból ered, hogy az őket definiáló algebrai utasítás alkata más. A

σ

esetében a képpont koordinátái a tárgypont koordinátáinak racionális függvényei. Az ilyen transzformációt racionális transzformációnak nevezzük. A

ϱ

esetében az is igaz, hogy a tárgypont koordinátái a képpont koordinátáinak racionális függvényei, ami pedig a

σ

esetében nem igaz. Ezért a

ϱ

-t biracionális transzformációnak nevezzük.
A biracionális transzformációk elmélete az ún. algebrai geometria egy gazdag és fontos fejezete. Ezt az elméletet (

1863

-ban) L. Cremona dolgozta ki, ezért nevezik a biracionális transzformációt Cremona-féle transzformációnak is.
Most megvizsgáljuk, hogy milyen hatással van a

ϱ

transzformáció a sík egyeneseire. A transzformációra nézve fixpont az olyan pont, amely a képével egybeesik. Könnyű belátni, hogy az

y

-tengely minden pontja fixpont, és más fixpont nincs. Ebben az értelemben mondhatjuk, hogy ennek az egyenesnek a képe önmaga. Hasonlóképpen az

y

-tengellyel párhuzamos bármely egyenesnek a képe önmaga, mert a

ϱ

transzformáció az egyenesen levő pont első koordinátáját nem változtatja meg. Ha azonban

x \neq 0

, akkor az

y

-tengellyel párhuzamos egyenesen levő bármely pontnak a második koordinátáját megváltoztatja; tehát az ilyen egyenesnek ugyan önmaga a képe, de nincs egy fixpontja sem. Az egyenest a transzformációra nézve invariáns egyenesnek mondjuk, hogyha a képével egybeesik.
A sík többi

l

egyenesének az egyenlete

\begin{matrix} y = m x + h \end{matrix}

alakú. Az ilyen egyenes pontjainak megfelelő képpontok alkotják az egyenes képét. A képvonal egyenletét az

l

egyenes egyenletéből a

(2)

szerint kifejezett

x

és

y

behelyettesítésével kapjuk:

\begin{matrix} \dot{y} = {\dot{x}}^{2} + m \dot{x} + h . \end{matrix}

(4)

Ez pedig egy olyan parabolának az egyenlete, amely az

y = x^{2}

egyenletű parabolából egy alkalmas

τ

eltolással származtatható.
Az a

τ

eltolás ugyanis, amely a

(0, 0)

pontot a

(- \frac{m}{2}, - \frac{m^{2}}{4} + h)

pontba viszi át, az

\begin{matrix} \dot{x} & = x - \frac{m}{2}, \\ \dot{y} & = y - \frac{m^{2}}{4} + h \end{matrix}

utasítással fejezhető ki. Az

y = x^{2}

egyenletű parabola pontjainak a

τ

szerinti képpontjai valóban az

\begin{matrix} \dot{y} + \frac{m^{2}}{4} - h = {(\dot{x} + \frac{m}{2})}^{2}, \end{matrix}

vagyis

\begin{matrix} \dot{y} = {\dot{x}}^{2} + m \dot{x} + h \end{matrix}

egyenletű parabola pontjait szolgáltatják.

ϱ

transzformáció alkalmazása. Vegyük észre, hogy a

ϱ

transzformációról eddig tárgyalt tudnivalókkal megközelítettük e cikk magvát képező problémát: a

Σ^{Θ}

affin tulajdonságainak a megállapítását és igazolását. Hiszen az "egyeneseket'' realizáló vonalakat ‐ egyeneseket és parabolákat ‐ az euklideszi sík egyeneseiből egy-egyértelműen származtathatjuk a

ϱ

transzformáció segítségével. Az a tény, hogy a

Σ

pontalakzat és a

Σ^{Θ}

pontalakzat között létesített bijekció, a

ϱ

transzformáció, az egyenesek és "egyenesek'' között is bijekciót indukál, fontos és szerencsés eredménynek mondható.
Egy további fontos tény az, hogy a

ϱ

transzformáció a tárgyalakzaton fennálló relációk némelyikét a képalakzatra átörökíti. Az ilyeneket a transzformációra nézve invariáns relációknak nevezzük. A legfontosabbat az előző tárgyalás során már láttuk: az illeszkedés a

ϱ

-ra nézve invariáns. Ez azt jelenti, hogy egy képpont akkor és csak akkor van rajta egy képvonalon, ha a képpont őse rajta van a képvonal ősén. Az

(\dot{x}, \dot{y})

képpont ugyanis akkor van rajta a képvonalon, ha igaz az

\dot{y} = {\dot{x}}^{2} + m \dot{x} + h

egyenlőség. Ebből pedig az

(1)

szerint

x^{2} + y = {\dot{x}}^{2} + m \dot{x} + h

, vagyis

y = m x + h

következik, ami azt jelenti, hogy a képpont őse, az

(x, y)

pont rajta van a képvonal ősén, az

y = m x + h

egyenesen. Azt pedig, hogy az

(x, y)

pont

y = m x + h

egyenesen való elhelyezkedéséből a képpont képegyenesre való illeszkedése következik, már

(4)

levezetésével elintéztük. Ugyanez a két állítás az

y

-tengellyel párhuzamos egyenesek esetében nyilvánvalóan igaz.
Az illeszkedés invariáns voltából következik, hogy a párhuzamosság is invariáns reláció. Persze definiálni kell a vonalak párhuzamosságát, mégpedig úgy, hogy az az egyenesek párhuzamosságára már elfogadott definícióval megegyezzék: két vonal párhuzamos, ha nincs közös pontjuk. Legyen

f

g

két egyenes és

\dot{f}

\dot{g}

ϱ

transzformációval előállított képük. Ha

f ∥ g

, de

\dot{f}

és

\dot{g}

egy közös

\dot{S}

ponttal rendelkezne, akkor az

\dot{S}

őse, az

S

pont ‐ az illeszkedés invariáns voltának következtében ‐ mind az

f

, mind a

g

egyenesen rajta volna, tehát

f ∥ g

Az invariánsokról szóló két tételünket a következő rövid alakban írhatjuk:
(i)

P \in f \Leftrightarrow \dot{P} \in \dot{f}

,
(ii)

f ∥ g \Leftrightarrow \dot{f} ∥ \dot{g} .

Tekintsük most újra az affin síkot definiáló

A_{1}

A_{2}

A_{3}

és

A_{4}

axiómákat. Lényegében véve mindegyik illeszkedésre, párhuzamosságra vonatkozó állítás. Minthogy pedig ezek a relációk a

ϱ

transzformációra nézve invariánsak, azért a

Σ

-ra érvényes axióma érvényes a

Σ

-ból

ϱ

által származtatható

Σ^{Θ}

-ra is. Ezzel tehát bebizonyítottuk, hogy a

Σ^{Θ}

alakzat egy Desargues-féle affin sík.
Ennek az egyszerű bizonyításnak a lényege a következő három észrevétel:
A

Σ^{Θ}

alakzat az euklideszi síkból a

ϱ

biracionális transzformációval származtatható.
Az axiómák illeszkedésre és párhuzamosságra vonatkozó állítások. Az illeszkedés és a párhuzamosság a

ϱ

-ra nézve invariáns.
A szóban forgó probléma különféle megoldásainak összehasonlító elemzése érzékeltethetné a

ϱ

transzformációval okoskodó eljárás erejét, előnyét. E helyett a próbára tett tanulók és egyetemi hallgatók dolgozatait elemezzük. Ebből kiderül, hogy a megoldást produkáló résztvevők miért tartották az

A_{4}

axiómára vonatkozó kérdés tisztázását "különösen nehéznek''.

A megoldók dolgozatainak elemzése. Minthogy más módszert nem ismertek, az analitikus geometria kezdetleges módszereit alkalmazták. A geometriai állításokat lefordították a koordináta-geometria nyelvére, azután képletről képletre való következtetés útján, ami szétágazó esetek végiggondolását követelte, haladtak a bizonyítandó állítást kifejező képlet felé. Itt az általuk produkált megoldás gondolatmenetét csak röviden vázoljuk.
Először azt állapították meg, hogy a

Σ^{Θ}

alakzat "egyenesét'' ábrázoló egyenesnek vagy parabolának az egyenlete

\begin{matrix} x = a, illetőleg y = x^{2} + b x + c \end{matrix}

alakú. Két ilyen egyenesnek nincs közös pontja. Egy ilyen egyenesnek és parabolának mindig van, de csak egy közös pontja. Két ilyen,

\begin{matrix} y = x^{2} + b_{1} x + c_{1}, y = x^{2} + b_{2} x + c_{2} (c_{1} \neq c_{2}) \end{matrix}

egyenletű parabolának aszerint, hogy

b_{1} \neq b_{2}

vagy

b_{1} = b_{2}

, egyetlenegy közös pontja van vagy egy sincs. Az utóbbi esetben a két parabola bármelyikét szimmetriatengelye mentén eltolhatjuk a másik parabolába; ebben az esetben mondjuk, hogy a két parabola párhuzamos egymással.
Ez után három aritmetikai állítást igazoltak.
1) Ha

x_{1} \neq x_{2}

, akkor az

y_{1} = x_{1}^{2} + b x_{1} + c

, és az

y_{2} = x_{2}^{2} + b x_{2} + c

b

c

-ben elsőfokú egyenletnek

(b, c)

-re egy és csak egy megoldása van.
2) Ha

b

x_{0}

y_{0}

tetszőlegesen adott számok, akkor az

y_{0} = x_{0}^{2} + b x_{0} + c

egyenlőségnek egy és csakis egy

c

szám tesz eleget.
3) A másodfokú

\begin{matrix} y = x^{2}, y = x^{2} - 2 x, y = x^{2} - 4 x + 4 \end{matrix}

egyenletek páronként a

(0, 0)

(2, 0)

(1, 1)

számpárokat határozzák meg.
Az pedig, hogy a

Σ^{Θ}

alakzaton

A_{1}

A_{2}

A_{3}

teljesül, rendre az

1)

2)

3)

következménye. Ebben a gondolatmenetben szokatlanul nagy munkát követel az

A_{4}

igazolása. A sikeresen dolgozó diákok egyöntetűen kijelentették: "nagyon nehéz''. Az

A_{4}

állításának a koordináták nyelvén való kifejezése szövevényes, a vele való okoskodást a bonyolult képletből bonyolult képletre vezető következtetés megnyújtja. Ezt még tetézi az a kombinációs szerteágazás, ami abból ered, hogy a

2.

ábrán szereplő egyeneseket a

Σ^{Θ}

alakzaton egyenesek is, meg parabolák is képviselhetik. A lehetséges kombinációk végiggondolása tovább növelte a bizonyítás terjedelmét. Ez a megoldásra vállalkozó diákok többségét visszariasztotta, a

A_{4}

érvényességét végül is nem bizonyították.