| Cím: | A bűvös hatszög | ||
| Szerző(k): | Bakos Tibor | ||
| Füzet: | 1978/október, 71 - 72. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az alábbi történetből láthatjuk majd, hogy csakúgy, mint a zenének, a matematikának is van ,,szórakoztató'' ága, ami sokszor épp olyan nehéz, mint a ,,komoly'' matematika. A ,,szórakoztató'' matematika egyik kedvenc témája a bűvös négyzetek vizsgálata. Egy angol hivatalnok, Clifford W. Adams, 1910-ben felvetette magának a kérdést, hogy milyen bűvös hatszögek léteznek. Arra hamar rájött, hogy az 1. ábra hét hatszögébe nem lehet az számokat úgy beírni, hogy az összeg minden egyenes mentén ugyanaz legyen, hiszen ez az ábra jelölései mellett miatt és egyenlőségét jelentené. 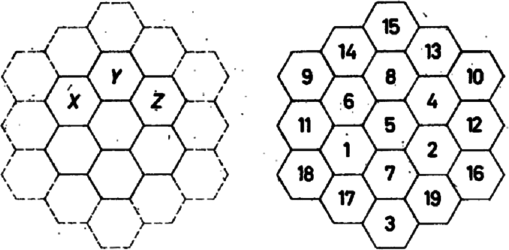 1. ábra, 2. ábra Kiegészítette hát az ábrát még egy sor hatszöggel, és azt kezdte vizsgálni, beírhatók-e az új ábra mezőibe az számok úgy, hogy az összeg minden egyenes mentén ugyanannyi legyen. Nem tudta, hogy az általa felvetett probléma megoldása már 1889-ben megjelent a Zeitschrift für Math. und Naturwiss. Unterricht című német folyóirat 20. kötetében. C. Adams vasúti tisztviselő volt, és a kérdéssel csak szabad idejében foglalkozott. Azzal gyorsította próbálkozásait, hogy a számokat kis hatszöglemezre írta, és ezeket tologatta az ábrán. Kísérletezését azonban csak közel negyven év múlva, 1957-ben koronázta siker. Már nyugdíjban volt, és épp kórházban feküdt egy operáció után, amikor végre talált egy megfelelő elrendezést. Legnagyobb bánatára azonban azt a papírlapot, amelyikre felírta élete fő eredményét, valahogyan elvesztette. Újabb sikertelen próbálkozások következtek, míg 1962-ben ha nem is talált újabb elrendezést, de legalább megtalálta az első sikeres elrendezést tartalmazó papírlapot 2. ábra Most már elküldte ezt egy matematikusnak, Triggnek, aki nekilátott további hatszögek keresésének. Hiába kutatott azonban, újabb elrendezést ő sem talált. 1963 decemberére aztán sikerült bebizonyítania, hogy nemcsak a 2. ábra lemezeit nem lehet úgy átrendezni (triviális szimmetriáktól eltekintve), hogy az összeg minden egyenes mentén ugyanannyi legyen, hanem akárhány további gyűrűt vonunk is az 1. ábra hatszögei köré, a kapott alakzatokba már nem lehet az egészeket -től kezdve úgy beírni, hogy az összeg minden egyenes mentén ugyanannyi legyen. Egy kérdés az olvasóhoz is: be tudná-e bizonyítani, hogy a bűvös hatszögnek szükségképpen mezejének kell lennie ? |