| Cím: | 1978. A XX. Nemzetközi Matematikai Diákolimpia feladatainak megoldása | ||
| Szerző(k): | Csirmaz László | ||
| Füzet: | 1978/október, 49 - 55. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Nemzetközi Matematikai Diákolimpia | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. feladat. Az és természetes számokra . Az , valamint tízes számrendszerbeli alakjában az utolsó három jegy sorrendben is megegyezik. Keressük meg azt az -et és -et, amelyre a lehető legkisebb ! (Kuba, 6 pont) Megoldás. A feltétel akkor és csak akkor teljesül, ha
A -tel való oszthatósághoz vizsgáljuk először utolsó jegyét értékekre. Ezek rendre azaz négyes periódust alkotnak. Így akkor és csak akkor osztható -tel, ha osztható -gyel. Az utolsó két számjegye ötös periódust alkot: tehát pontosan akkor osztható -tel, ha többszöröse -nek. Végül utolsó három jegyét vizsgálva először esetén kapunk -tel osztható végződést. Ez azt jelenti, hogy ha osztható -tel, akkor értékének legalább -nak kell lennie. Ezt az előző feltétellel összevetve azonnal látható, hogy a keresett értékek és . Megjegyzés. A feladat megoldásához felhasználhatjuk az ún. Euler-tételt: ha és relatív prímek, és -val jelöljük a -nál kisebb, -hoz relatív prím egészek számát, akkor osztható -val. (Lásd például Molnár Emil: Matematikai versenyfeladatok, 488. oldal.) Mivel és és relatív prímek, azért osztható -tel. Ez azonban nem jelenti azt, hogy a legkisebb ilyen kitevő, noha a feladat éppen a legkisebbet kérdezte. 2. feladat. Egy gömb belsejében adott egy pont. A gömb felszínén úgy helyezkednek el az , pontok, hogy és páronként merőlegesek egymásra. Legyen a és által meghatározott téglának -vel szemközti csúcsa . Mi a pontok mértani helye ? (USA, 7 pont.) Megoldás. Először egy könnyen igazolható segédtételt mondunk ki: minden téglalapra és minden (nem feltétlenül a téglalap síkjában lévő) pontra . Legyen ugyanis (a1. ábra), ekkor , hiszen és merőlegesek. A bizonyítandó állítás pedig az 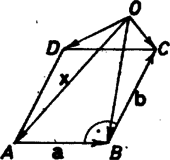 1. ábra 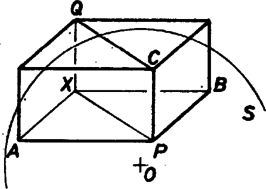 2. ábra Térjünk rá a feladatra. Legyen az adott gömb középpontja , sugara , az téglalap negyedik csúcsa (2. ábra). A segédtételt az , valamint téglalapokra alkalmazva kapjuk, hogy ahonnan  3. ábra Megmutatjuk, hogy az gömb minden pontja hozzátartozik a mértani helyhez. Tekintsük ugyanis az gömb és a átmérőjű gömb metszésvonalát. Ennek az síkba eső egyik pontja legyen és -t téglalappá kiegészítő negyedik pont (3. ábra). A segédtétel szerint , azaz az pont kívül van az gömbön. Így az átmérőjű gömbnek valamint az gömbnek a -ben -re emelt merőleges síkban van két közös pontja: az egyik legyen , az -t téglalappá kiegészítő negyedik csúcs . Az , szakaszok páronként merőlegesek, az általuk meghatározott tégla negyedik csúcsa , továbbá és az gömbön van. Elegendő tehát megmutatnunk, hogy is -en van. Ez viszont az Megjegyzés. Ha nem azt követeljük meg, hogy és egy gömb felszínén legyenek, hanem hogy rendre három egymással koncentrikus gömb felszínén, a mértani hely továbbra is egy gömb felülete. A feladat tetszőleges dimenziójú gömbökre, például síkra is általánosítható. 3. feladat. A pozitív egész számok halmaza megegyezik az I. megoldás. Tekintsük az 1 és közti egész számokat. Ezek mindegyike vagy -nek vagy -nek valamilyen helyen felvett értékeként adódik ki. Mégpedig értékeként szám, alapján értékeként szám, . Ezzel minden és közti számot pontosan egyszer kapunk meg, tehát
II. megoldás. A (*) összefüggés alapján
III. megoldás. Legyen , és . Ekkor és a (**) képlet szerint
Mivel és , azért és így alkalmazhatjuk az indukciós feltevést: A teljes indukció befejezéséhez még -ot például -re ellenőrizni kell: , s ez valóban teljesül. Végül minden -nél nagyobb pozitív szám egyértelműen írható fel alakban, ahol . Ekkor alapján Megjegyzés. A megoldásokban feltételeztük, hogy létezik a feltételeket kielégítő és függvény. Annyit bizonyítottunk, hogy ha létezik, akkor lehet csak. A megoldásokból az is kiderült, hogy legfeljebb egy ilyen és függvény létezhet. IV. megoldás. Legyen és . Állítjuk, hogy és eleget tesz a feladat összes feltételének. Így (feltéve, hogy és egyértelműen meghatározott) . Először is világos, hogy és szigorúan monoton növekszik, hiszen és . Másrészt , és irracionális, és így és értékkészlete minden egész számot pontosan egyszer ad ki (lásd Skljarszkij‐Csencov‐Jaglom: Válogatott feladatok és tételek az elemi matematika köréből, 1. kötet, 108. feladat). Így csak a és alapján az egyenlőtlenséget -val osztva és átrendezve 4. feladat. Az háromszögben . Egy kör belülről érinti az háromszög köré írt kört, továbbá az oldalt a , az oldalt a pontban. Bizonyítsuk be, hogy a szakasz felezőpontja az háromszög beírt körének középpontja. (USA, 5 pont). 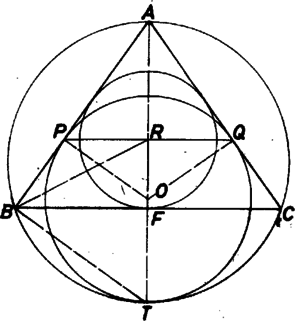 4. ábra Megoldás. Jelöljük az érintő kör középpontját -val, az érintési pontot -vel, felezőpontját -fel és felezőpontját -rel (4. ábra). Az ábra szimmetriája folytán az pontok mind rajta vannak a háromszög szimmetriatengelyén. , hiszen mindkettő az érintő kör sugarával egyenlő, ezért a hasonló és derékszögű háromszögekből 5. feladat. Álljon az sorozat különböző pozitív egész számokból. Bizonyítsuk be, hogy minden természetes számra Megoldás. Először megmutatjuk, hogy ha van olyan számpár, amelyekre , akkor az egyenlőtlenség bal oldalát csökkenthetjük azzal, hogy -t és -t felcseréljük. Ugyanis a változás Megjegyzés. Ugyanezzel a gondolatmenettel látható be a következő állítás is: ha 6. feladat. Egy nemzetközi társaságnak tagja van különböző országból. A tagokat -től -ig számozták meg. Mutassuk meg, hogy legalább egy olyan tag van, akinek a sorszáma megegyezik két honfitársa sorszámának összegével, vagy kétszer akkora, mint egy honfitársa sorszáma. (Hollandia, 8 pont). I. megoldás. Tegyük fel, hogy az állítás nem igaz, ebből ellentmondásra fogunk jutni. Mivel , azért valamelyik országból, -ból legalább tagnak kellett jönnie, legyenek sorszámaik II. megoldás. A következő állítást igazoljuk teljes indukcióval: ha egy legalább csúcsú teljes gráf éleit színnel kiszínezzük, akkor biztosan lesz benne egyszínű háromszög (azaz három csúcs úgy, hogy köztük bármely él ugyanolyan színű). 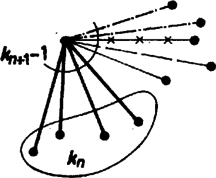 5. ábra Tekintsünk most egy csúcsú gráfot, melynek csúcsai -től -ig vannak megszámozva. Az és csúcs közti élet hat különböző szín valamelyikével színezzük ki, attól függően, hogy az sorszámú tag melyik országból jött. Mivel , azért van egyszínű háromszög, a csúcsok száma legyen . Ekkor a és a sorszámú tagok ugyanabból az országból valók, és , ahogyan azt kívántuk. Megjegyzések. 1. Elképzelhető, hogy . Ekkor nem három, hanem csak két tag sorszámát kapjuk, de az egyik sorszám éppen kétszer akkora, mint a másik. 2. A második megoldásból az is kiolvasható, hogy ország esetén ha a társaságnak legalább tagja van, létezik a kérdezett tulajdonságú tag. Igazolható, hogy ha -nel jelöljük a legkisebb olyan tagszámot, amelyre ilyen tulajdonságú társaság létezik, akkor |