Cím: 1977. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Surányi János 
Füzet: 1978/február, 50 - 57. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Bizonyítsuk be, hogy ha p5-nél nagyobb prímszám, akkor az
x4+4x=p
egyenletnek nincs egész megoldása.
 
Megoldás. Csak pozitív egészek jönnek tekintetbe, mert negatívokra a
K=x4+4x
kifejezés nem is egész, 0-ra pedig 1. Pozitív páros számokra K osztható 4-gyel, tehát összetett.
Ha x pozitív páratlan szám, akkor 2y+1 alakban írva
4x=4⋅42y=4(2y)4.

Írjunk 2y=2x-12 helyébe z-t, akkor kifejezésünk így alakítható:
K=x4+4z4=x4+4z4+4x2⋅z2-4x2z2=(x2+2z2)2-(2xz)2==(x2+2z2+2xz)(x2+2z2-2xz)=((x+z)2+z2)((x-z)2+z2).
Itt az első tényező mindig nagyobb, mint 1, mert mindegyik tagja legalább 1. A második tényező pedig csak akkor lehet 1, ha x=z=1. Mivel
x=2y+1z=2y,
így ez abban az egy esetben következik be, ha x=1, y=0. Ekkor
x4+4x=5,
p azonban 5-nél nagyobb. Így a feladatban szereplő egyenletnek valóban nincs egész megoldása.
 
Megjegyzések. 1. A bizonyítás a feladat állításánál lényegesen többet adott, könnyen kiolvasható belőle a következő:
Ha x és z tetszés szerinti egész szám, akkor
N=x4+4z4
csak akkor nem összetett, ha
|x|=1ész=0vagy|z|=1.

Valóban, mivel x is, z is páros kitevőn szerepel, a negatív értékeket abszolút értékükkel helyettesíthetjük. Ha x=0, akkor N=4z4 összetett (z=0-ra N=0). Ha pedig z=0, akkor |x|=1-re N=1, |x|>1-re összetett.
2. Az itt használt azonosságon alapult az 1969. évi Nemzetközi Matematikai Diákolimpia 1. feladatának1 megoldása. Erre több versenyző is utalt.
3. Sokan észrevették, hogy ha x páratlan és nem osztható 5-tel, akkor x4 (tíz alapú számrendszerben felírva) 1-re végződik, 4x pedig 4-re, tehát x4+4x osztható 5-tel és ha x>1, akkor nagyobb 5-nél. Nem tudtak azonban mit kezdeni azzal az esettel, ha x az 5 páratlan többszöröse.
 
Második feladat. Az ABC háromszög A-ból induló súlyvonala a körülírt kört A1-ben metszi. A1 tükörképe BC felezőpontjára A2. Ugyanígy képezzük B-ből, illetve C-ből kiindulva a B2, illetve C2 pontot.
Bizonyítsuk be, hogy A2, B2, C2 és a háromszög M magasságpontja egy körön van.
 
I. megoldás. 1. Megmutatjuk, hogy az M magasságpontnak a BC oldal F1 felezőpontjára vonatkozó M1 tükörképe az ABC háromszög köré írt körön van, annak éppen az A-val átellenes pontja.
Ebből már könnyen fog következni a feladat állítása.
B és C egymás tükörképe F1-re. Ha M különbözik a B és C csúcstól, akkor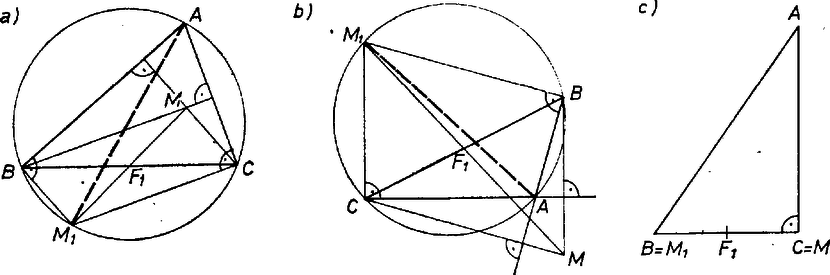
M1B‖MCésM1C‖MB,
mert pontra való tükrözés egyenest vele párhuzamos egyenesbe visz át (1a és b ábra). Azonban MC az AB oldalra bocsátott magasság egy szakasza, MB pedig az AC oldalra bocsátotté, így
ABM1∢=ACM1∢=90∘,
tehát B és C rajta van az AM1 mint átmérő fölé rajzolt körön. Az ABC háromszög köré rajzolt kör azonban egyértelműen meg van határozva, így azonos az AM1 átmérőjű körrel, tehát M1 a háromszög köré írt körnek A-val átellenes pontja, amint állítottuk.
 
 

1. ábra
 

Az állítás akkor is igaz, ha pl. M=C (1c. ábra). Ez ugyanis azt jelenti, hogy
AC⊥BC,
a háromszög derékszögű. M tükörképe F1-re B-vel esik egybe, és ez valóban az A-val átellenes pont.
2. A bizonyított tételből következik, hogy A2, B2 és C2 az M pont merőleges vetülete a háromszög súlyvonalain. Elég ezt pl. A2-re belátni. Ha 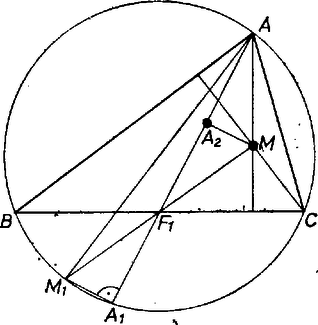M1≠A1, akkor
F1A1M1∢=AA1M1∢=90∘,
mert AM1 átmérő (2. ábra). Tükrözve F1-re, kapjuk, hogy
F1A2M∢=90∘,
és ezt állítottuk. Ha A1=M, akkor A2=M, tehát ekkor is igaz az állítás.
 
 

2. ábra
 

Tudjuk, hogy a háromszög súlyvonalai egy ponton mennek keresztül, a háromszög S súlypontján. Ha S≠M, akkor A2, B2 és C2 az SM átmérőjű körön van. Ha S=M ‐ ez csak a szabályos háromszögre teljesül ‐, akkor egybeesik velük A2, B2 és C2 is; és van végtelen sok kör, amelyik mindegyik pontot tartalmazza.
Azt bizonyítottuk tehát be, a feladat állításán túlmenve, hogy minden háromszöghöz van olyan kör, amelyik átmegy A2-n, B2-n, C2-n, a háromszög magasságpontján és súlypontján.
 
II. megoldás. Jelöljük a háromszög köré írt kör középpontjából az A, B, C, A1, B1, C1, A2, B2, C2 és M ponthoz mutató vektorokat rendre a, b, c, a1, b1, c1, a2, b2, c2, ill. m-mel. Közülük az első hat hossza egyenlő, a kör sugara.
Megmutatjuk, hogy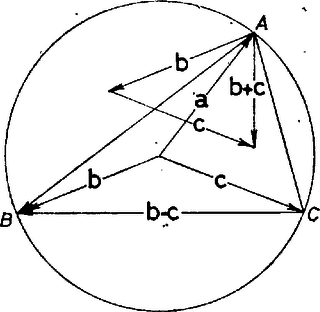
m=a+b+c.
Jelöljük N-nel azt a pontot, amelynek a jobb oldali vektor a helyvektora (3. ábra). Ekkor
AN→=b+c,CB→=b-c.
Ha ezek egyike sem 0 nulla-vektor, akkor merőlegesek, mert egy olyan rombusz átlóvektorai, amelynek az oldalvektorai felváltva ±b-vel, ill. ±c-vel egyenlők. Vagy mert skaláris szorzatuk:
(b+c)⋅(b-c)=b⋅b-c⋅c=|b|2-|c|2=0.
Az AN egyenes tehát a BC-re merőleges magasság egyenese.
 
 

3. ábra
 

Mivel B és C különböző pontok, így
b-c≠0.
Ha b+c=0, akkor N=A, s így ekkor is rajta van N az A-ból húzott magasságvonalon. Ugyanígy látható, hogy N rajta van a másik két magasságvonalon is, tehát azonos a háromszög magasságpontjával. Ezt akartuk belátni.
Azt, hogy A2 az A1 tükörképe a BC szakasz középpontjára, a következő vektoregyenlőség fejezi ki:
12(a1+a2)=12(b+c).
Innen
a2=b+c-a1.
Most már könnyen láthatjuk, hogy
MA2⊥AA1,(1)
ugyanis
MA→2=a2-m=-(a+a1),AA→1=a1-a.
a és a1 egyenlő hosszú vektorok. Ebből a fentebbi meggondoláshoz hasonlóan adódik, hogy vagy M=A2, vagy teljesül az (1) összefüggés. Ebből pedig következik a feladat állítása, amint azt az I. megoldásban láttuk.
 
Megjegyzés. Érdekes megoldás adódik a feladatra komplex számok segítségével. A komplex számok eközben csak arra fognak szolgálni, hogy átfogalmazzuk segítségükkel az állítást egy könnyen belátható geometriai állítássá.
 
A komplex számokról a következőket használjuk fel. Ugyanazok a számolási szabályok érvényesek rájuk, mint a valós számokra.
A komplex számok a sík vektoraival szemléltethetők. Ebben a szemléltetésben az összeadást a vektorösszeadás szemlélteti.
Két komplex szám hányadosát ábrázoló vektor hajlásszöge a pozitív abszcisszatengelyhez az osztó irányszögével kisebb mint az osztandó irányszöge.
A valós számokat az abszcissza-tengelyen szemléltetjük, ezek irányszöge tehát 0∘ vagy 180∘ (vagy ezektől 360∘ egy egész többszörösével különbözhet).
Legyen most már A, B, C, D a sík négy különböző pontja, a helyvektoraik által szemléltetett komplex számok a, b, c, d. Ha a négy pont egy körön van, akkor a CAD∢ és CBD∢ vagy egyenlő és egyirányú, vagy 180∘-ra egészíti ki egymást és ellentétes irányú (4. ábra). Ugyanez áll tehát a
d-ac-aésd-bc-b(2)
komplex számok irányszögére is. Ez azt jelenti, hogy a
d-ac-a:d-bc-b=(d-a)(c-b)(c-a)(d-b)(3)
hányados irányszöge 0∘ vagy 180∘, ez a szám tehát valós. Ez akkor is igaz, ha d=a, vagy c=b. Ez azt jelenti, hogy legalább 2 pont egybeesik. Ekkor pedig a pontokon át lehet kört rajzolni, kivéve ha három egy egyenesen levő pontunk van.
 
 

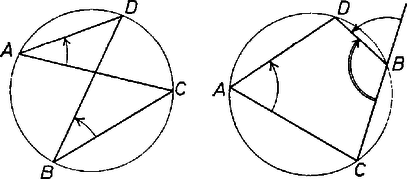4. ábra
 

Tegyük most fel, hogy a (3) szám 0-tól különböző és valós. Ekkor a (2) alatti (komplex) számok is 0-tól különbözők, és irányszögeik vagy egyenlők vagy 180∘-kal különböznek. Lehet mind a két szám valós, de ha egyik nem az, akkor a másik sem az.
Ha mind a kettő valós, akkor A, C és D is, B, C és D is egy egyenesen van, tehát a négy pont egy egyenesen van. Ha viszont a (2) számok nem valósak, akkor a szögekre nyert összefüggés éppen azt jelenti, hogy ABCD húrnégyszög, a négy pont egy körön van. A következőt nyertük tehát:
A (3) komplex szám akkor és csak akkor valós, ha A, B, C, D egy körön vagy egy egyenesen van. Az alábbiakban ezt fogjuk felhasználni.
 
III. megoldás (komplex számok felhasználásával). Válasszuk a háromszög köré írt kör középpontját a komplex számsík 0 pontjának és az A, B, C, A1, B1, C1, A2, B2, C2, M pontok ábrázolják rendre az a, b, c, a1, b1, c1, a2, b2, c2, m komplex számokat. Ekkor, mint az előző megoldásban, adódnak az
a2=b+c-a1b2=c+a-b1,c2=a+b-c1m=a+b+c
összefüggések. Ha a négy pont egy körön van, akkor a következő komplex szám valós:
(a2-c2)(b2-m)(b2-c2)(a2-m)=(c+c1-(a+a1))(-(b+b1))(c+c1-(b+b1))(-(a+a1))=(a+a1-(c+c1))(b+b1)(b+b1-(c+c1))(a+a1).(4)
Az utolsó tört valós volta viszont azt jelenti, hogy az
a+a1,b+b1,c+c1és0
komplex számokat ábrázoló pontok egy körön vagy egy egyenesen vannak. Az utolsó pont a háromszög köré írt kör középpontja.
Mivel a és a1 abszolút értéke (az ábrázoló vektorok hossza) egyenlő, így a 0-t, a-t, a1-et és (a+a1)-et ábrázoló pontok egy rombusz csúcsai. Ekkor azonban az (a+a1)-et ábrázoló pont az O pont tükörképe a rombusz másik két csúcsát összekötő egyenesre, vagyis az AA1 súlyvonal egyenesére. Jelöljük ezt A'-vel (5. ábra), hasonlóan a (b+b1)-et és (c+c1)-et ábrázoló B' és C' pont az O pont tükörképe a háromszög B-ből, ill. C-ből induló súlyvonalára.
 
 

5. ábra
 

Nyilvánvaló azonban, hogy O, A', B', C' egy körön van, mert a három súlyvonal átmegy a háromszög S súlypontján. Ez a pont tehát mind a három tükrözésnél helyben marad, s így
SO=SA'=SB'=SC'.
Ekkor a (4) tört értéke valós, viszont
a+a1-(c+c1)b+b1-(c+c1)
nem valós, mert A', B' és C' nincs egy egyenesen. Az utolsó tört azonban éppen az
a2-c2b2-c2
tört, tehát ez sem valós, A2, B2, C2 nincs egy egyenesen. Ebben az esetben A2, B2, C2 és M-nek kell egy körön lennie, és ezt akartuk bizonyítani.
 
Harmadik feladat. Három iskola mindegyikében n tanuló van. Minden tanuló a másik két iskolából együttvéve n+1 tanulót ismer. Bizonyítsuk be, hogy választható a három iskola mindegyikéből egy-egy tanuló úgy, hogy mindegyikük ismeri a másik kettőt. (Az ismeretségeket kölcsönösnek tételezzük fel.)
 
I. megoldás. Megkérdezünk mindenkit, hány ismerőse van egy-egy iskolában. Legyen a legkisebb hallott szám k. Ez nem 0, mert mindenkinek több ismerőse van a másik két iskolából, mint ahány tanuló jár egy-egy iskolába.
Legyen mondjuk András az A iskolából egy tanuló, akinek k ismerőse van a B iskolában; ekkor a C iskolában n+1-k ismerőse van, és k-1 tanulót nem ismer.
András egy B iskolabeli ismerőse, mondjuk Bálint legalább k tanulót ismer a C iskolából. Ezek közül legalább egy ismeri Andrást is. Ha Csongor egy közös ismerős, akkor hármuk közül mindenki ismeri a másik kettőt. A feladat állítása tehát igaz.
 
Megjegyzés. A feladat állítása akkor is igaz, ha a feltételt úgy módosítjuk, hogy minden tanulónak legalább n+1 ismerőse van a másik két iskolában. Ekkor a bizonyítás annyiban módosul, hogy Andrásnak a C iskolában legalább n+1-k ismerőse van, s így legfeljebb k-1 tanulót nem ismer. A gondolatmenet további része változatlanul érvényes.
Nem vezethetjük vissza a módosított állítást az eredetire úgy, hogy egyes ismeretségeket figyelmen kívül hagyunk. Lehetséges ugyanis, hogy Andrásnak pl. több mint n+1 ismerőse van a másik két iskolában, azonban mindegyik ismerőse csak n+1 tanulót ismer a másik két iskolából. Ekkor András bármelyik ismeretségét figyelmen kívül hagyva, volt ismerősének már csak n ismerőse marad a másik két iskolában.
 
II. megoldás. A megjegyzésben említett általánosabb állítást bizonyítjuk, amelyik szerint:
Ha minden tanuló a másik két iskolában együtt legalább n+1 tanulót ismer, akkor kiválasztható mindegyik iskolából egy-egy tanuló úgy, hogy mindegyikük ismerje a másik kettőt.
A bizonyítást teljes indukcióval végezzük.
Ha történetesen mindegyik iskolának csak 1‐1 tanulója van, akkor a feltétel éppen azt kívánja, hogy mindegyikük ismerje a másik kettőt.
Legyen most m>1 és tegyük fel, hogy minden n<m természetes számra igaz az állítás, ha az iskolákba n gyerek jár. Legyen továbbá A, B és C három iskola, amelyek mindegyikébe m tanuló jár és mindegyikük legalább m+1 tanulót ismer a másik két iskolából.
Az A iskola a1 tanulója ismerje a B iskolából b1-et, ő a C iskolából c1-et. Ha c1 ismeri a1-et, akkor ő hármukra teljesül a feladat állítása. Ha nem, akkor c1 egy A-beli ismerőse legyen a2 és folytassuk az eljárást mindig ugyanebben a sorrendben véve az iskolákat, míg egy olyan tanulóhoz nem érünk, aki egyszer már szerepelt a felsorolt ismerősök közt. Ez a tanuló és az utána felsoroltak egy olyan kört alkotnak, amelyben mindenki ismeri a szomszédait és amelyikhez mindegyik iskolának ugyanannyi tanulója tartozik. Legyen ez a szám k. Ha k=1, ez azt jelenti, hogy teljesül a feladat állítása.
Ha k=m (a kör tartalmazza az összes tanulót), akkor válasszunk ki egy tanulót, pl. az A-beli a1-et. A körben szomszédos B és C-beli tanulók m párt alkotnak, amelyek bi, c, (i=1,2,...,m) tanulói ismerik egymást. (A 6. ábra a tanulókat ponttal, az ismeretséget összekötéssel szemlélteti.)
 
 

6. ábra
 

Mivel a1-nek a két iskolában legalább n+1 ismerőse van, így legalább egy pár mindkét tagját ismeri. Ekkor azonban erre a 3 tanulóra teljesül a feladat állítása.
Ha 1<k<m, akkor nézzük az iskoláknak a körhöz nem tartozó tanulóit. Minden iskolában (m-k)-an vannak. Ha mindegyiküknek legalább m-k+1 ismerőse van a másik két iskola megmaradt tanulói közt, akkor az indukciós feltétel szerint kiválasztható a feladat állítását kielégítő három tanuló.
Ha pl. az A iskolabeli ak+1-nek a B és C iskolában megmaradt tanulók közt legfeljebb m-k ismerőse van, akkor a körnek legalább k+1B-be és C-be járó tanulóját ismeri. Ezeket azonban a kör most k darab ismerősökből álló párba sorolja, s így ak+1 ismer legalább egy ilyen párt. Minden esetben találtunk tehát a feladat állítását kielégítő hármast. Ezzel az indukciós bizonyítást befejeztük.
 
Megjegyzések. 1. Ez a bizonyítás nem alkalmas a feladatnak az eredeti formában való bizonyítására, mert a bizonyítás második részében, ha minden tanulónak m+1 ismerőse van, és az iskolánként k tanulót tartalmazó kört kivéve, a visszamaradó tanulók közül senki sem ismer a körből k-nál több tanulót, akkor lehetnek, akik a körből k-nál kevesebb tanulót ismernek és így a visszamaradók közül (m-k+1)-nél többet. Ha viszont bebizonyítottuk ezt az általánosabb állítást, az tartalmazza speciális esetként az eredetit is.
2. Nyilvánvalóan nem elég, ha csak annyit teszünk fel, hogy minden tanulónak n ismerőse van a másik két iskolában. Legyen minden iskolában páros számú tanuló, mondjuk mindegyikben m fiú és m lány. Ha az A iskola lányai ismerik a B iskolából a lányokat, a C-ből a fiúkat, az A-ba járó fiúk a B-ből a fiúkat, a C-ből a lányokat, továbbá a B-ből és C-ből a lányok a lányokat, a fiúk a fiúkat, akkor mindenkinek annyi ismerőse van, ahány gyerek egy-egy iskolába jár, de nincs a feladat követelményeit kielégítő három tanuló.
Ha az egy-egy iskolába járó tanulók száma páratlan, akkor nem is lehet mindenkinek pontosan annyi ismerőse, ahányan egy iskolába járnak, hiszen akkor mindenkit megkérdezve ismerősei számáról, minden ismeretséget kétszer vennénk számba, viszont páratlan számú tanuló mindegyike páratlan számú ismerőst említene, ami együtt ismét páratlan számot adna.
3. Felmerülhet az a kérdés is, hogy megvalósítható-e tetszés szerinti tanulószám mellett a feladat eredeti feltétele. A válasz igenlő. Egy lehetőség a megvalósításra a következő. Ha páratlan számú tanuló, n=2m-1 van iskolánként, akkor sorszámozzuk iskolánként a tanulókat. Az A iskola minden tanulója ismerje a B és a C iskola vele egyenlő sorszámú tanulója utáni m tanulót, úgy értve, hogy ha a sor végére érünk, akkor az elejéről folytatjuk. Ekkor a B és a C iskola minden tanulója A-ból a vele egyező sorszámú tanuló előtti m tanulót ismeri. Ismerje továbbá a B iskola minden tanulója C-ből a vele egyező sorszámú tanuló utáni m tanulót. (Ekkor a C-beli tanulók B-ből a velük egy sorszámú tanuló előtti m tanulót ismerik.) Ekkor minden tanulónak 2m=n+1 ismerőse van.
Ha viszont minden iskolába n=2m tanuló jár, mondjuk m fiú és m lány, akkor ismerjék egymást a különböző iskolabeli lányok a különböző iskolabeli fiúkkal, továbbá az A iskolabeli fiúk ismerjék a B iskolából a velük egy sorszámú lányt, a B-beli fiúk a C-beli velük egy sorszámú lányt, és a C-beli fiúk az A-beli velük egy sorszámú lányt. Ekkor mindenkinek 2m+1=n+1 ismerőse van. Természetesen számos más lehetőség is van a feltételek megvalósítására.
1Lásd pl. Bakos T. ‐ Lőrincz P. ‐ Tusnády G.: Középiskolai Matematikai Versenyek, 1969. 109‐110. old.