Cím: Számítástechnika 15. rész
Szerző(k):  Ada-Winter Péter 
Füzet: 1978/május, 216 - 221. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feladatok:

 

1. Szubrutinok készítendők FEEL, HUR és SZEL azonosítóval. Mindegyikük átveszi a nem negatív A gyökalapot, a P és Q kezdeti intervallum végpontokat, továbbá a pozitív EPS hibakorlátot. A rutinok a három módszer szerint számítják a B-vel jelölt gyökértéket és számolják a menetek számát.
2. Keret-program készítendő, amely kártyáról olvassa be A, P, Q, EPL értékeit, mindhárom szubrutinnal számíttatja a gyököket és kinyomtatja ‐ az alkalmazott módszer feltüntetésével ‐ a gyökök értékeit és az előállításhoz szükséges menetek számát.
3. Készítsünk szöveges összehasonlító elemzést a három négyzetgyök-közelítő módszerről!
 


Megoldások (összevontan tárgyalva):
 


Mindhárom gyökközelítő eljárásnál kikötjük, hogy a (p,q) intervallumban a függvénynek pontosan egy gyöke legyen. Igaz, hogy az eljárásokon alapuló programok esetleg akkor is számítanak gyököt, ha több van belőlük a megadott intervallumban. Ilyenkor p és q megadott értékeitől függ, hogy melyik gyököt számítja ki, de előfordulhat az is, hogy a program végtelen ciklusba ragad. A gyök közelítése mindhárom módszernél úgy történik, hogy képezünk a (p,q) intervallumban egy pontot (melyet b-vel jelölünk), és meghatározzuk, hogy a kettéosztott intervallum melyik részébe esik a gyök.
Ezt az újabb (pi,qi) részintervallumot tekintjük kiindulásnak, és ezen belül újabb b pontot képezünk stb., miközben pi<b<qi minden esetben.
Ha adott egy ε hibakorlát, akkor ezzel a közelítés kétféle módon képzelhető el: vagy az |pi-qi|≤ε, vagy az |f(b)|≤ε feltétel teljesüléséig folytatjuk az eljárást. A programokban mindkét feltétel teljesülésére nézve vizsgálatot kell tartanunk, mivel előfordulhatnak a következő esetek: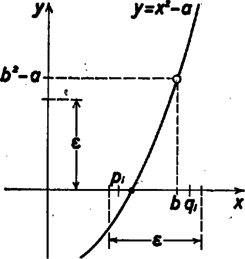
 

 

1. ábra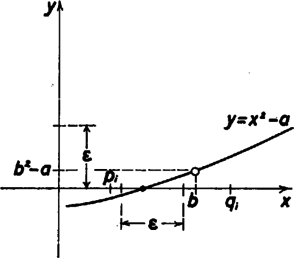
 

 

2. ábra

 

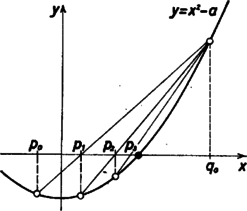‐Ha a gyöknél a függvénygörbe érintőjének meredeksége nagy (1. ábra), akkor a |pi-qi|≤ε feltétel teljesülése mellett a függvény értéke egy közbeeső b-nél még messze nem zérus, azaz |f(b)|>ε. Viszont ha az eljárást az |f(b)|≤ε feltétel teljesüléséig akarnánk folytatni, akkor esetleg |pi-qi| oly kicsivé válik, hogy a gépi ábrázolhatóság határán kívül esik. Ilyenkor a kerekítésekből eredően ugyancsak könnyen ciklusba ragad a program.

‐		Ha a gyöknél a függvénygörbe érintőjének meredeksége kicsi (2. ábra), akkor az |f(b)|≤ε feltétel teljesülése esetén |pi-qi|>ε. Ha a függvény értéke majdnem zérus az intervallum végpontjában, akkor ez az újabb b kiszámításánál túlcsordulást okozhat, amikor f(pi)-vel vagy f(qi)-vel osztani kell.

 

 

3. ábra

 


A feladatok megoldásánál tehát mindkét feltétel teljesülését figyelnünk kell. Az elmondottakból az is nyilvánvaló, hogy a kétféle feltétel kikötése, illetőleg teljesülése korántsem jelent azonos közelítési pontosságot. Ezért ε-t olyan hibakorlátnak kell tekintenünk, amelyik bármelyik feltétel teljesülése esetén kielégíti pontossági igényeinket. E kérdés további részletezésébe nem bocsátkozhatunk.
A felezési eljárás szubrutinjában B-t (ami b-nek felel meg) P és Q számtani közepéből kapjuk, ezért függvényértékeikre előzetes vizsgálatot nem tartunk. Amennyiben P és B függvényértékei az x tengely azonos partjára esnek, vagyis szorzatuk pozitív, akkor a gyök B és Q közé esik, ezek lesznek az új intervallum-végpontok. Ellenkező esetben P és B határozza meg az új intervallumot. Ha a függvényértékek szorzata kivételesen pontosan zérussá válna, akkor elegendő P függvény értékére vizsgálatot tartani és ennek megfelelően kell B értékét megadni, mely után az eljárás befejeződik. N jelöli a B képzéseinek a számát, ha ez az érték felhasználásra kerül. A mindezt tartalmazó blokkdiagramot az 5. ábrán láthatjuk.
A húrmódszernél észrevehetjük, hogy az eljárás során az intervallum egyik végpontjának helye változatlan. (Esetünkben ez a Q.) Ez látható a 3. ábrán. A B pont ilyenkor mindig a legutoljára képzett húr‐tengely metszéspont. Számítására az y-y1=y2-y1x2-x1⋅(x-x1) képletet használtuk fel, melyből x-et fejeztük ki y=0 mellett. Miután a számítás során kapott abszcissza értékekhez tartozó függvényértékekkel osztunk, ezekre nézve vizsgálatot kell tartani. Az eljárás blokkdiagramját a 7. ábrán látjuk, melyben a PONT utasításfüggvény számítja a húr és az abszcissza metszéspontjának x koordinátáját.
A szelő-módszer (melyet Osztrovszkij-módszernek is szoktak nevezni), mint már említettük, úgy módosítja a húr-módszert, hogy a pi és a pi+1 pontokhoz tartozó függvénygörbe pontokon áthaladó szelőnek és az x tengelynek metszéspontjában képezi az új qi+1 pontot (4a ábra). Ezzel a módszerrel két nehézség adódhat. Egyik, hogy a szelő a ,,túloldalon'' metszi ki az új qi+1-et (4b ábra). Ez minden olyan esetben bekövetkezik, amikor a húr meredekségének (m1) és a szelő meredekségének (m2) az előjele különböző, azaz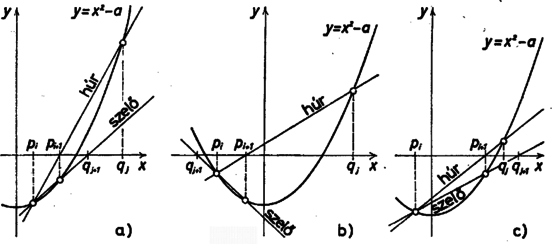
sign(m1)≠sign(m2).

 

 

4. ábra

 

Az eljárásból az ilyen eseteket ki kell hagynunk. A másik, hogy a meredekségek előjelei egyezőek ugyan, de a szelő qj-nél távolabb metszi ki a qj+1 pontot (4c ábra). Ez olyan esetekben áll elő, amikor a húr abszolút értékben vett meredeksége nagyobb a szelőénél, azaz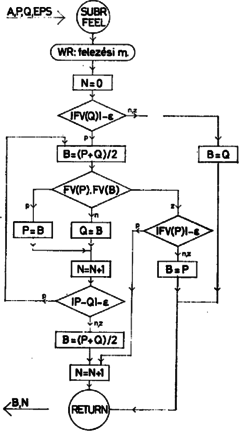
|m1|>|m2|.
Az ilyen esetet is el kell kerülni. A kihagyott esetekben a húrmódszerrel közelítünk.
 

 

5. ábra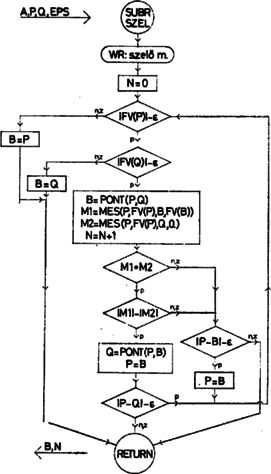

 

 

6. ábra

 

A szubrutinban az előbbiekben már használt PONT és az egyenesek meredekségét számító MES utasításfüggvény szerepel. Utóbbi az m=y2-y1x2-x1 képlet értékeit számítja.
Ebben az eljárásban minden olyan függvényértéket vizsgálnunk kell, amely osztóként előfordul. A blokkdiagramot a 6. ábrán láthatjuk. Ezek után a keretprogram és a szubrutinok egy előállítási lehetősége az alábbi: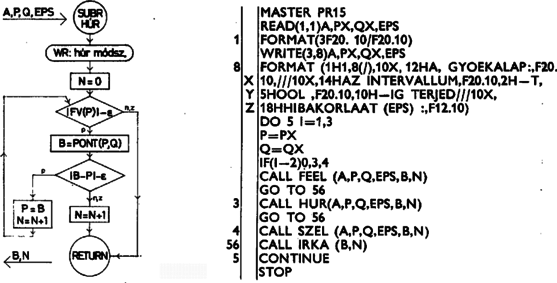
 

 

7. ábra

 

MASTER PR15  READ(1,1)A,PX,QX,EPS  1  FORMAT(3F20. 10/F20.10)WRITE(3,8)A,PX,QX,EPS  8FORMAT (1H1,8(/),10X, 12HA, GYOEKALAP:,F20.X10,///1OX,14HAZ INTERVALLUM,F20.10,2H-T,Y5HOOL ,F20.10,10H-IG TERJED///1OX,Z18HHIBAKORLAAT (EPS) :,F12.10)DO 5 I=1,3  P=PXQ=QXIF(I-2)0,3,4CALL FEEL (A,P,Q,EPS,B,N)GO TO 56  3CALL HUR(A,P,Q,EPS,B,N)GO TO 56  4  CALL SZEL (A,P,Q,EPS,B,N)  56CALL IRKA (B,N)  5CONTINUESTOPENDSUBROUTINE FEEL (A,P,Q,EPS,B,N)WRITE (3,3)  3FORMAT (////1OX,17HFELEZÉSI ELJÁRÁS:)N=0IF(ABS(FV(Q,A))-EPSF) 0,0,2B=QGO TO 5  2B=(P+Q)/2.IF(ABS(FV(B,A)*  FV(P,A))-EPS) 6,6,0IF(FV(B,A)*  FV(P,A)) 0,0,4Q=BGO TO 13  4P= B  13N=N+1IF(ABS(P-Q)-EPS 0,0,2B=(P+Q)/2.  50N=N+1RETURN  6IF(ABS(FV(P,A))-EPS) 0,0,50B=P  5RETURNENDSUBROUTINE HUR(A,P,Q,EPS,B,N)PONT(R,S)=((R-S)*  FV(R,A))/(FV(S,A)-FV(R,A))+RWRITE(3,4)N=0B=P  2IF(ABS(FV(P,A))-EPS) 5,5,0B=PONT(P,Q)IF (ABS(B-P)-EPS) 1,1,0P=BN=N+1GO TO 2  1N=N+1  5RETURN  4FORMAT(///10X,11HHURMODSZER:)ENDSUBROUTINE SZEL (A,P,Q,EPS,B,N)REAL M1,M2,MESMES(X1,Y1,X2,Y2)=(Y2-Y1)/(X2-X1)PONT(R,S)=((R-S)*  FV(R,A))/(FV(S,A)-FV(R,A))+R  WRITE(3,51)N=0  2IF(ABS(FV(P,A))-EPS)3,3,0IF(ABS(FV(Q,A))-EPS)1,1,0B=PONT(P,Q)N=N+1M1=MES(P,FV(P,A),B,FV(B,A))M2=MES(P,FV(P,A),Q,0.)IF(M1*  M2)10,10,0IF(ABS(M1)-ABS(M2))10,10,0Q=PONT(P,B)P=BIF(ABS(P-Q)-EPS)5,5,2  10IF(ABS(P-B)-EPS)5,5,0P=BGO TO 2  3B=P  RETURN  1B=Q  5RETURN  51FORMAT(///1OX,14HSZELŐ MODSZER:)ENDSUBROUTINE IRKA(B,N)WRITE(3,7)B,N  7FORMAT(30X,7HA GYOK:,F20.10,5X,16HA MENETEK SZAMA:,I4)RETURNENDFUNCTION FV(X,A)FV=X**  2-ARETURNENDFINISH  
Néhány tájékoztató adat a három módszer összehasonlítására:
‐A hibakorlát logaritmusának (azaz a kitevőnek) csökkenésével a menetek száma mindhárom módszer esetén nagyjából lineárisan növekszik. A növekedés mértéke azonban jelentősen különbözik, és pl. ε=10-9 esetében a felezési módszer 33, a húrmódszer 27, a szelő-módszer 6 ciklusban közelíti a gyököt.
‐1-től 10-ig növelve az intervallum hosszát a felezési módszernél 14-től 17-ig, a húr-módszernél 3-tól 17-ig, a szelő-módszernél 2-től 8-ig növekedett a menetek száma, közel lineárisan.

 

8. A Newton ‐ Raphson-féle iterációs módszer
 

8.1 Négyzetgyökszámítás Newton ‐ Raphson módszerrel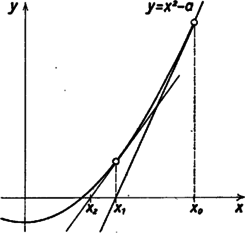
 

 

8. ábra

 


A négyzetgyök meghatározásának egy az előbbieknél is gyorsabb eljárását láthatjuk az alábbiakban. Legyen adva az y=x2-a parabola és egy nem a gyökre eső x0 pont az abszcisszán, melyet kezdő értéknek fogunk nevezni (lásd 8. ábra). Húzzuk meg a függvénygörbéhez az x0 pontnál az érintőt és jelöljük ennek az abszcisszával alkotott metszéspontját x1-gyel. Ezen pont felett a függvénygörbéhez újabb érintőt húzunk mely az abszcisszából az x2-es pontot metszi ki, és ezt az eljárást folytatjuk. Az (x0,x02-a) ponton áthaladó egyenesek egyenletei:
y-(x02-a)=m⋅(x-x0).
Ha az egyenesek közül az érintőt akarjuk kiválasztani, akkor ennek meredeksége a függvénynek x0 pontban vett első deriváltja kell hogy legyen. A metszéspont x koordinátáját kifejezve kapjuk, hogy:
x1=12⋅(x0+ax0).
Miután az eljárás ismétlődik, az i+1-dik lépésben kapott pont:
xi+1=12⋅(xi+axi).
Ezt nevezzük a a érték közelítő sorozatát előállító Newton ‐ Raphson-képletnek. Az olyan eljárást, melyben egy számítási eredmény közelítő értékeinek konvergens sorozatát úgy nyerjük, hogy bármelyik elem a sorozat ezt megelőző eleméből számítható, iterációnak nevezzük. A sorozat képzéséhez mindig meg kell adni az x0 kezdőértéket.
 


Feladatok
 


1) Állítsa elő a harmadik, negyedik, és ötödik gyököket közelítő sorozat Newton ‐ Raphson képleteit.
2) Készítsen szubrutint, amely Newton ‐ Raphson eljárással négyzetgyök közelítő értéket számít. A NR2 azonosítójú szubrutin átveszi az A-val jelölt alapot, a Q-val jelölt kezdőértéket és a hibakorlátot.
3) Melyek a Newton ‐ Raphson eljárás alkalmazhatóságának szükséges feltételei?
 

Értesítjük kedves Olvasóinkat, hogy az 1978‐79. tanév során a KÖMAL Számítástechnikai Szakkört indít az alább felsorolt szerdai napokon: szeptember 27., október 25., november 22., január 24., február 28., március 28., április 25. és május 23. A szakkör minden alkalommal 1630-tól 19 óráig tart, helye a Munkaügyi. Minisztérium Számítástechnikai Intézete, Budapest, VIII. ker. Reguly Antal u. 57‐59., B épület, III. emelet 302-es terem. (1630 után az épülettömbbe a Könyves Kálmán körút 48‐52. szám alatt lehet bejutni.)
A szakkörön tanároknak, számítástechnikai szakembereknek és középiskolai hallgatóknak lehetőséget kívánunk nyújtani olyan előadások megtartására vagy feladatok bemutatására, amelyek a középiskolai ismeretekre építhetők. A szakkörök alkalmával korlátozott időtartamban futtatási lehetőséget is tudunk biztosítani. Kérjük, hogy mindazok, akik a szakkörön előadást kívánnak tartani, illetőleg feladatot óhajtanak bemutatni, legalább két hónappal az esedékes időpont előtt lépjenek érintkezésbe a Számítástechnikai Rovat vezetőjével. (A szeptemberi szakkör esetében július 10-ig.)
 

Misi pajtás, sétálhatnál?1

 

Hatan vannak a híres magánintézet bennlakó növendékei: Kálmán, László, Mihály, Nándor, Oszkár és Péter. Mihály volt köztük minden tekintetben a legéletrevalóbb. Aki feladatában megakadt, Misitől kért tanácsot. De a játékban is ő volt a legügyesebb, labdázásnál, viaskodásnál is mindenki az ő pártjára vágyott. Az igazgató is minden vizsgálaton megdicsérte őt. Szemében mégsem Misi volt az intézet első növendéke. Misinek legfényesebb feleletei sem bírtak az igazgató arcára oly ragyogó fényt varázsolni, mint amilyen gyönyörűség látszott rajta, mikor László és Oszkár gazdag atyjától vadkan érkezett ajándékba. A két testvér mindenütt előnyben részesült.
A hétköznapi séták előtt is László és Oszkár nyilatkozhattak először, sétálni akarnak-e vagy inkább az intézményben méltóztatik-e maradniok. Csak azután vetették fel Misinek a séta vagy nem-séta kérdését. Akkor pedig már kicsinyes rendtartási szabályok korlátozták szabad választását. Ezek pedig a következők voltak:
 

I. Hétfőn és kedden sohasem engedték meg négy vagy több tanulónak a sétát.
II. Viszont csütörtökön, pénteken és szombaton nem volt szabad három vagy több növendéknek az intézetben maradnia.
III. Ha kedden, szerdán vagy szombaton Misi Lászlóval akart tartani, ezt csak akkor tehette meg, ha Kálmán, Oszkár és Péter is velük lehetett.
IV. Ha hétfőn vagy szombaton László sétálni ment, akkor vagy Nándor tartozott az intézetben maradni, vagy Misi, Oszkár és Péter.
 

Egy szerdai napon László és Oszkár valamin összevesztek. Oszkár duzzogott, s mikor László sétálni ment, nem ment vele, pedig gyönyörű idő volt. Misi bizony szívesen tartott volna Lászlóval, de a rendtartási szabályok nem engedték meg. Azonfelül a kis haragos avval fenyegetődzött: ,,Fogsz te ezen a héten többször is itthon maradni''.
Misi egy ideig hallgatott, azután Oszkár ismételt ingerkérdéseire nemmel felelt. Oszkár visszafeleselt, végre fogadásra került a dolog. Ki nyerte a fogadást?
1A feladat a Mathematikai és Physikai Lapok kiadott első kötetében jelent meg.