Cím: Számítástechnika 13. rész
Szerző(k):  Ada-Winter Péter 
Füzet: 1978/március, 117 - 121. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az előző részben kitűzött feladatok megoldása:

 

1. Feladat: Blokkdiagram készítendő a 10 ismeretlenes egyenletrendszer eliminációs eljárása során alkalmazandó főelem keresésére.
Megoldás: új főelem keresésére, mint említettük, akkor kerül sor, ha az közel zérus értékű, emiatt a vele való osztás túlcsordulást, a program futásának leállását eredményezné. A megfelelő főelem megtalálása után oszlopcserét hajtunk végre és folytathatjuk az eliminációt. Azt azonban "föl kell íratnunk'', hogy az oszlopok sorrendje miként változott, mivel a visszahelyettesítésnél a kapott gyökök sorrendje a cserélt oszlopok sorrendjével lesz azonos. A gyököket az eredeti sorrendbe csak ennek segítségével rendezhetjük.
Miután így a Gauss-féle eliminációs módszerre épülő program a visszahelyettesítési és ellenőrzési résztől eltekintve elkészült, bemutatjuk a teljes program első részének egy lehetséges formáját. Ezzel kapcsolatos megjegyzéseink a következők:
‐ A MASTER szegmens az A és B tömböket tölti fel az eredeti együttható mátrixszal (utóbbit az ellenőrző részben használjuk fel). × lesz az eredmény vektor, a NYOM vektor az oszlopok sorrendjét tárolja, indulásnál az 1-től 10-ig terjedő egész számokkal töltjük fel. LX az SCR1 szubrutinnak, NX az SCR3 szubrutinnak ad jelzést. SCR1 az eredeti, ill. a 9-dik menet után kapott együttható mátrixot írja ki. ELIM2 a főelemkereséssel módosított eliminációs szubrutin. VISSZ a visszahelyettesítő, CONTR az ellenőrző, SCR3 az eredményt kijelző szubrutinok, melyekről a következő részben esik szó.
‐ ELIM2-ben L a menet számát jelzi. A főelemet a FOEL szubrutin keresi ki. A K =10 utasítás után a 9-edik menetet követő egyenletrendszer megoldhatóságát vizsgáljuk. Ha K értéke 10, az SCR2 kiíratja az elimináció elkészültét, és visszatér a hívó programba, de ha K értéke 11 vagy 12, akkor jelzi az egyenletrendszer megoldhatatlanságának okát és a STOP-ra fut. A szubrutin blokkdiagramját az 1. ábra mutatja.
 



 

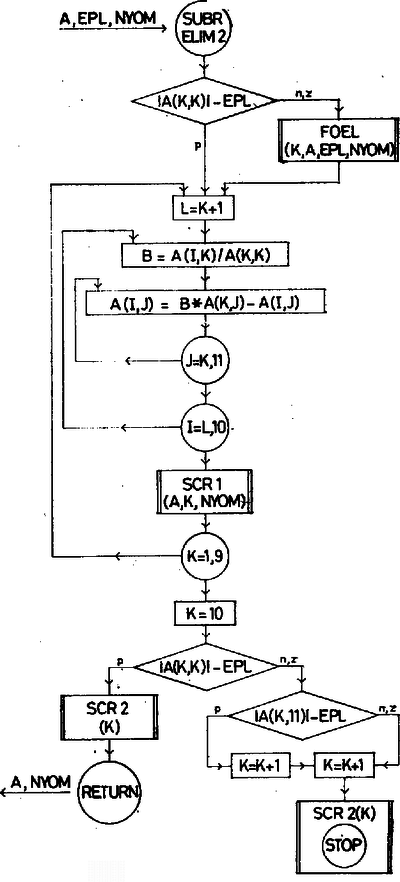1. ábra

 

‐ A FOEL a főelemet egy k-dik menetben a (k+I)-edik (J-edik) oszloptól a 10-edik oszlopig keresi. Ha a sorban legalább 10 együttható zérus, akkor az SCR2 rutint hívja és ott nyomtatás után megáll. Az oszlopcsere a 3-as címkéjű ciklusutasítással kezdődik. A cserélt oszlopok indexeit a NYOM vektor megfelelő komponenseinek cseréjével jegyezzük fel. Blokkdiagramját a 2. ábra mutatja.
 



 

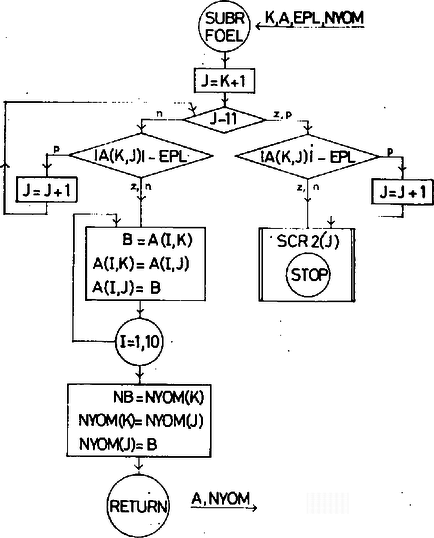2. ábra

 
‐ A SCR2 csak akkor engedi vissza a program végrehajtást a hívó szegmensbe, ha K=10, azaz ha az eliminációban mindig van zérushoz nem közel eső főelem. Ha a sorban mind a 11 együttható zérussá válik, akkor valamelyik egyenlet előállítható a többiből, ha csak az első tíz zérus, de a 11-edik nem az, akkor van két egymásnak ellentmondó egyenlet.
Ezek után a Gauss-féle eliminációs program első része az alábbi:
 

        MASTER PR13DIMENSION A(10,11),B(10,11),X(14),NYOM(10)READ(1,1)((A(I,J),J=1,11),I=1,10)  1FORMAT(9(6F12.2/5F12.2/),6F12.2/5F12.2)DO 3 I=1,10NYOM(I)=IDO 3 J=1,11  3B(I,J)=A(I,J)EPL=10.**(-3)LX=0NX=-1CALL SCR1(A,LX,NYOM)CALL ELIM2(A,EPL,NYOM)CALL VISSZ(A,X,NYOM)CALL SCR3(X,NX)CALL CONTR(B,X)STOPENDSUBROUTINE SCR1(A,L,NYOM)DIMENSION A(10,11),NYOM(10)IF(L-1) 0,6,6WRITE(3,1)  1FORMAT(1H1////20X,28HAZ EREDETI EGYUETTHATOO MAAT,×4HRIX:///)GO TO 4  6IF(L-9) 8,0,8WRITE(3,5) L  5FORMAT(1H1////20X,i2,10H‐DIK MENET///)  4WRITE(3,7)((A(I,J),J=1,11),I=1,10),(NYOM(K),K=1,10)  7FORMAT(10(//7X,11 F12.2),///20X,×21HAZ OSZLOPOK HELYZETE:,//15X,10I12/)  8RETURNENDSUBROUTINE ELIM2(A,EPL,NYOM)DIMENSION A(10,11),NYOM(10)DO 3 K=1,9IF(ABS(A(K,K))‐EPL) 0,0,4CALL FOEL(K,A,EPL,NYOM)  4L=K+1DO 2 I=L,10B=A(I,K)/A(K,K)DO 1 J=K,11  1A(I,J)=B*A(K,J)‐A(I,J)  2CONTINUECALL SCR1(A,K,NYOM)  3CONTINUEK=10IF(ABS(A(K,K))‐EPL) 5,5,0CALL SCR2(K)RETURN  5IF(ABS(A(K,11))‐EPL) 7,7,0K=K+1  7K=K+1CALL SCR2(K)ENDSUBROUTINE SCR2(K)WRITE(3,2)IF(K‐11) 0,5,7RETURN

  5WRITE(3,6)        WRITE(3,9)STOP  7WRITE(3,6)WRITE(3,8)STOP  2FORMAT(///50X,18HELIMINAACIOO KEESZ/)  6FORMAT(///50X,19HAZ EGYENLETRENDSZER/)  8FORMAT(5X,14HELLENTONDASOS)  9FORMAT(5X,12HHATAROZATLAN)ENDSUBROUTINE FOEL(K,A,EPL,NYOM)DIMENSION A(10,11),NYOM(10)J=K+1  4IF(J‐11) 1,0,0IF(ABS(A(K, J))‐EPL) 6,6,0J=J+1  6CALL SCR2(J)  1IF(ABS(A(K,J))‐EPL) 0,0,3J=J+1  3DO 5 I=1,10B=A(I,K)A(I,K)=A(I,J)  5A(I,J)=BNB=NYOM(K)NYOM(K)=NYOM(J)NYOM(J)=NBRETURNEND

 

2. feladat. Program készítendő egy 5×5-ös méretű bűvös négyzet betöltésére és kinyomtatására.
 

Megoldás: egy lehetséges program az alábbi:
 

        MASTER PR14DIMENSION A(5,5)READ(1,9) AK,DM=1N=3DO 8 J=1,5DO 7 I=1,5A(M,N)=AKAK=AK+DIF(M‐5) 0,1,0M=M+1GO TO 2  1M=1  2IF(N‐5) 0,3,0N=N+1GO TO 7  3N=1  7CONTINUEIF(N‐1) 0,4,0N=N‐1GO TO 8  4N=5  8CONTINUEOESSZ=0.DO 5 I=1,5  5OESSZ=OESSZ+A(I,3)WRITE(3,6) ((A(I,J),J=1,5),I=1,5),OESSZ  6FORMAT(1H1,20(/),5(50X,5F12.2//),50X,×40HA SOR- ILL. OSZLOPOSSZEGEK KOZOS ERTEKE:,×3X,F12.2)  9FORMAT(2F12.2)STOPEND  
 

A feladatban nem adtuk meg az elsőként betöltendő, "kezdő'' mátrix elem indexeit, emiatt az tetszőleges. A közölt programban a kezdő elem sor-, ill. oszlopindexeit az M, ill. N azonosítók értékadással kapják. Ha megfelelően adjuk meg az indexeket, akkor nem csak a sorok és oszlopok összege "bűvös'' (ugyanaz a szám), hanem a fő-, ill. mellékátlókra eső elemek összege is. Ilyenkor diagonálisan bűvös a négyzet, ami a példában adott kezdőelem indexekkel is bekövetkezik. A bűvös négyzet további speciális tulajdonsága lehet, hogy a fő-, ill. mellékátlókkal párhuzamos "tört átlók'' mentén elhelyezkedő elemek összege is bűvös, azaz pándiagonális a négyzet. A példánkban a mellékátlókkal párhuzamos tört átlókra ez is fennáll. Pl. a2,1+a1,2+a5,3+a4,4+a3,5 egy ilyen mellékátlóval párhuzamos tört átló elemei. A kitöltés más "szabály'' alapján is történhet, pl. lóugrás szerint. Bizonyos páros rendű mátrixok is lehetnek bűvös négyzetek, ezek kitöltése bonyolultabb. Bűvös négyzetekkel rovatunk tovább nem foglalkozik.
 

6.2. folytatás. A főelem keresése a megoldás pontosságával is kapcsolatos. Ha mindig a legnagyobb abszolút értékű sor-elemet választjuk főelemnek, akkor növelni tudjuk a pontosságot. Sajnos még ilyen módszer mellett is előfordulhat, hogy az eljárás használhatatlanul pontatlan gyökökhöz vezet, ami a kiindulási mátrix bizonyos tulajdonságaival magyarázható. Ennek kifejtésébe nem bocsátkozhatunk.
 


6.3. Visszahelyettesítés, ellenőrzés
 

A visszahelyettesítő szubrutin az eliminált együtthatójú egyenletrendszerből "alulról fölfelé haladva'' kiszámítja a gyököket. Ezek sorrendje azonban a megcserélt oszlopok sorrendjével egyezik. Hogy végül tudjuk, melyik az első, második stb. gyök, a NYOM vektor segítségével helyre kell állítani sorrendjüket. Ezt is a visszahelyettesítő szubrutin végzi. A k-adik gyök egy olyan tört, melynek nevezője a sor fődiagonálisba eső eleme. A számlálót kéttagú kifejezésnek tekinthetjük, első tagja a k-adik sor 11-edik eleme, a második tagja egy C szám, melynek számítása a C=C+A(L+1,K)*Y(K)   utasítással történhet, ha C kezdőértéke zérus, és L értékét 10-től visszafelé (k+1)-ig változtatjuk.
A pontosság bizonytalansága miatt a B tömbben eltett eredeti együttható mátrix felhasználásával visszahelyettesítjük az eredmény vektor komponenseit az egyenletek bal oldalába, és a helyettesítési értékeket kivonjuk a jobb oldali számértékekből. Ha a különbségek egy kívánt pontossági intervallumba esnek, az eredmény vektort jónak mondjuk.
 

Feladatok
 

1. Írjuk meg a PR13 hiányzó szubrutinjait. (Az ellenőrző vektort is nyomtassa!)
2. A KÖMAL 55. kötet 2. száma 63. oldalán levő 2077-es feladatot módosítsuk az alábbi szerint: Két db egységnyi sugarú körlemez úgy fekszik egymáson, hogy együttvéve 6π egységnyi területet fednek le. Szorítsuk olyan két tört közé a középpontok távolságát, amelynek nevezője 1000, a számlálóik egészek, és a számlálóik különbsége 1. A feladat számítására készítsünk programot.