Kezdőlap


Cím:	Az 1977. évi (10.) Nemzetközi Fizikai Diákolimpia feladatai
Füzet:	1977/november, 161 - 166. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Egy négyütemű motor kompresszióviszonya $ε = 9, 5$ . A motor $27^{\circ} C$ hőmérsékletű, $ε V_{0}$ térfogatú levegőt és benzingőzt szív be $100 kPa$ nyomáson (1. ábra). Ezután sűrítés következik, az állapotábrán az $A$ pontból a $B$ pontba adiabatikusan jutunk el $(x = 1, 4)$ . A robbanáskor $(B - C)$ a nyomás megkétszereződik. A dugattyú kilökése közben $(C - D)$ a gázkeverék adiabatikusan terjed ki $ε V_{0}$ térfogatra. A kipufogószelep kinyílásakor a nyomás visszaesik a kezdeti $100 kPa$ értékre. A kompresszióviszony a henger legnagyobb és legkisebb térfogatának az arányát jelenti.
a) Határozzuk meg a nyomás és hőmérséklet értékeit az $A$ , $B$ , $C$ és $D$ állapotokban!
b) Mennyi a körfolyamat elméleti hatásfoka?

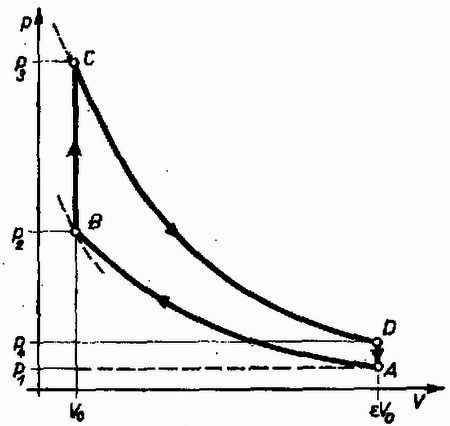1. ábra

Megoldás. Az adiabatikus állapotváltozás egyenlete ideális gázra

\begin{matrix} T V^{x - 1} = állandó. \end{matrix}

a) Az

A

állapotban a nyomás

P_{1} = 100 kPa

, a térfogat

ε V_{0}

, a hőmérséklet

T_{1} = 300 K

; a

B

állapot jellemzői

p_{2}

V_{0}

T_{2}

. Az adiabata egyenlete

\begin{matrix} T_{1} {(ε V_{0})}^{x - 1} = T_{2} V_{0}^{x - 1}, \end{matrix}

amiből

T_{2} = 738, 3 K

. Az ideális gáz állapotegyenletéből (

p V / T =

állandó) meghatározhatjuk a

B

állapotban levő gáz nyomását:

\begin{matrix} p_{2} = 2, 34 MPa . \end{matrix}

C

állapotban a nyomás

p_{3} = 2 p_{2} = 4, 68 MPa

, a térfogat

V_{0}

, a hőmérsékletet pedig az állapotegyenletből fejezhetjük ki:

T_{3} = 1476, 6 K

.
A

D

állapot paramétereit

(p_{4}

ε V_{0}

T_{4})

ismét az adiabatikus állapot. változás egyenletéből, illetve az állapotegyenletből kaphatjuk meg:

T_{4} = 600 K

;

p_{4} = 2 kPa

.
b) A hatásfokot megadó tört nevezője a

B - C

lépésben felvett hő, mert ezt kell az üzemanyag elégetésével biztosítani. A felvett hő a gáz energiájának növekedésével egyenlő, mert a térfogat változatlan, és így nincs munkavégzés. Tehát a felvett hő

c_{v} m (T_{3} - T_{2})

. A mechanikai munka alakjában hasznosított energia a

B - C

lépésben felvett és a

D - A

lépésben visszaadott hő különbsége:

\begin{matrix} c_{v} m (T_{3} - T_{2}) - c_{v} m (T_{4} - T_{1}) = c_{v} m (T_{1} + T_{3} - T_{2} - T_{4}) . \end{matrix}

A hatásfok:

\begin{matrix} η = \frac{c_{v} m (T_{1} + T_{3} - T_{2} - T_{4})}{c_{v} m (T_{3} - T_{2})} = 1 - \frac{T_{4} - T_{1}}{T_{3} - T_{2}} . \end{matrix}

Mivel

T_{3} = 2 T_{2}

és

T_{4} = 2 T_{1}

, a hatásfok egyszerűen

\begin{matrix} η = 1 - \frac{T_{1}}{T_{2}} . \end{matrix}

A - B

folyamatra felírt adiabata egyenletéből

T_{1} / T_{2} = ε^{1 - x}

, tehát a négyütemű benzinmotor hatásfoka:

\begin{matrix} η = 1 - ε^{1 - x} . \end{matrix}

A hatásfok csak a kompresszióviszonytól függ, azaz a hatásfokra vonatkozó b) kérdésre az a) alatti adatok kiszámítása nélkül is felelhetünk.
Számadatainkkal

η = 0, 59 = 59 %

. A valóságos hatásfok alig több, mint ennek a fele, mert sok hő távozik el a körfolyamatban való részvétel nélkül.

2. Egy szappanhártyát

α = 30^{\circ}

-os beesési szögben fehér fénnyel világítunk meg. A visszavert fényt túlnyomó részben

λ_{0} = 0, 5 μ m

hullámhosszú élénk zöld színben látjuk.
a) Mennyi a hártya lehetséges legkisebb vastagsága?
b) Milyen színűnek látszik ez a hártya merőleges irányból? A folyadék törésmutatója

n = 1, 33

Megoldás. a) A rétegbe bemenő, az

A

pontban megtört fény egy része

B

-ben visszaverődik,

C

-ben a levegőbe kilépve ismét megtörik, és az elég messze levő szemünkbe jut (2. ábra). A fényforrásból érkező

D C

sugár egy része is visszaverődik és az előbbi sugárral együtt jut a szemünkbe.

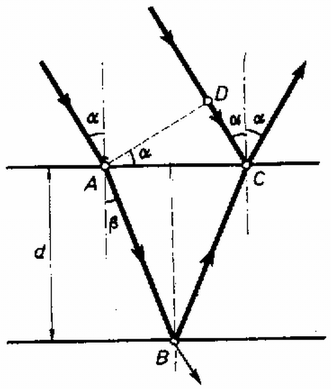2. ábra

A D

síkba az egész sugárnyaláb egyező fázissal érkezik. Az a kérdés, mekkora az útkülönbség, illetve a fáziskülönbség az alsó és felső határfelületekről érkező sugarak között, mert ettől függ, hogy az interferencia által erősítés vagy gyengítés jön-e létre, és a fehér fény különböző hullámhosszúságú fényei közül teljes intenzitással mi marad meg.
Az alul visszaverődő fénysugár útja

A

-tól

C

-ig

\bar{A B} + \bar{B C} = 2 d / cos β

. A közegben a hullámhossz

λ_{0} / n

, tehát ezen az úton az

A

-tól

C

-ig elférő hullámok darabszáma:

\begin{matrix} \frac{2 d}{λ_{0} (cos β) / n} = \frac{2 d n}{λ_{0} cos β} . \end{matrix}

A felül visszaverődő fénysugár útja

D

-től

C

-ig:

\begin{matrix} \bar{D C} = \bar{A C} sin α = 2 d tgβsinα= \\ = 2 d sin β sin α / cos β . \end{matrix}

Ezen a távolságon a

λ_{0}

hullámhosszból

2 d sin β sin α / (λ_{0} cos β)

darab fér el, de a nagyobb törésmutatójú anyagon történő visszaverődéskor

180^{\circ}

-os fázisugrás történik, tehát a

D C

távolságon elférő hullámok száma:

\begin{matrix} \frac{2 d sin β sin α}{λ_{0} cos β} + \frac{1}{2} . \end{matrix}

Erősítés akkor jön létre, ha a hullámok számának különbsége valamilyen

k

egész szám:

\begin{matrix} k = \frac{2 d n}{λ_{0} cos β} - \frac{2 d sin β sin α}{λ_{0} cos β} - \frac{1}{2} = \frac{2 d n}{λ_{0} cos β} (1 - sin^{2} β) - \frac{1}{2} = \frac{2 d n cos β}{λ_{0}} - \frac{1}{2} = \\ = \frac{2 d}{λ_{0}} \sqrt[]{n^{2} - sin^{2} α} - \frac{1}{2} . \end{matrix}

Ennek átalakítása után az erősítés feltétele:

\begin{matrix} \frac{4 d}{λ_{0}} \sqrt[]{n^{2} - sin^{2} α} = 2 k + 1. \end{matrix}

A törésmutatótól és a geometriai adatoktól függ, hogy mely hullámhosszra következik be a legnagyobb erősítés. Az ezzel szomszédos hullámhosszúságú fények sem oltódnak ki egészen, csak gyengülnek, tehát nem kapunk monokromatikus fényt. Ha

k

növekszik, a szín mindig kevésbé teltebb lesz, mert az egyik rendben való erősítést egy másik rendben történő gyengítés lerontja. Valamelyest vastagabb lemeznél szürkét kapunk. Ezért van az, hogy a ,,vékony lemezek színei'' csak vékony lemezeknél látszanak. Feladatunk élénk zöldet említ és a legvékonyabb hártya iránt érdeklődik, tehát

k = 0

veendő és a rétegvastagság:

\begin{matrix} d = \frac{λ_{0}}{4 \sqrt[]{n^{2} - sin^{2} α}} = 0,101 μ m . \end{matrix}

Megjegyzés. Ez a hártya olyan vékony, hogy egy

2 cm \cdot 3 cm

méretű keretbe férő tömege csak

0, 06 mg

lenne, a szokásos analitikai mérleggel nem volna megbízhatóan lemérhető.

b) Merőleges beesésnél,

k = 0

esetében a legjobban erősített hullámhossz

λ_{b} = 4 d \sqrt[]{n^{2} - sin^{2} 0} = 4 d n

volna. Az előbbi

d

-értéket felhasználva:

\begin{matrix} λ_{b} = λ_{0} \cdot \frac{n}{\sqrt[]{n^{2} - sin^{2} α}} = \frac{λ_{0}}{cos β} . \end{matrix}

d

-től függetlenül így lehet az

α

-hoz tartozó

λ_{0}

-ból a merőleges beeséshez tartozó

λ_{b}

-t kiszámítani. A mi esetünkben

λ_{b} = 1, 079 λ_{0} = 0, 540 μ m

, ami sárgásabb árnyalatú zöld színt jelent. De nemcsak a szemünket kell bevinni a beesési merőlegesbe, hanem lehetőleg a fényforrást is. A vékony lemezek színeinek vizsgálatakor éppen ezért nagy felületű, diffúz fényforrás célszerű, mint amilyen a borús ég, amikor eső után nézzük a pocsolyán az olajfoltokat.

3. Egy elektronágyú

U = 1000 V

feszültséggel gyorsított elektronokat bocsát ki az ,,

a

'' egyenes irányában (3. ábra). Az ágyútól

d = 5 cm

távolságban,

α = 60^{\circ}

-os irányban levő

M

céltárgyat akarjuk eltalálni. Ennek érdekében

B

indukciójú homogén mágneses teret alkalmazunk. Mekkora legyen ennek az erőssége,
a) ha a mágneses térerősség merőleges az ,,

a

'' egyenes és az

M

pont által meghatározott síkra;
b) ha a mágneses térerősség párhuzamos a

T M

iránnyal? Az elektron töltése

Q = 1, 6 \cdot 10^{- 19} C

, tömege

m = 9, 11 \cdot 10^{- 31} kg

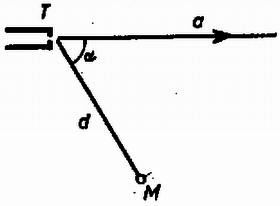3. ábra

Megoldás. a) A

v

sebességgel repülő elektront a merőleges irányú,

B

indukciójú homogén mágneses tér

r

sugarú körpályára tereli. E mozgáshoz szükséges

m v^{2} / r

erőt a

B v Q

nagyságú Lorentz-erő szolgáltatja. Homogén, állandó mágneses tér nem képes az elektron sebességének nagyságát megváltoztatni, mert az erő mindig merőleges a sebességre. A mi esetünkben a körpálya sugara a 4. ábra szerint

r = d / (2 s i n α)

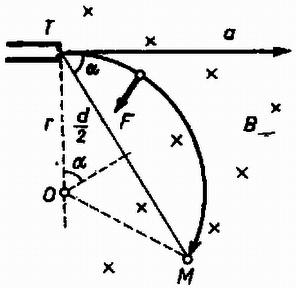4. ábra

Az elektronágyúból kirepülő elektron sebessége

m v^{2} / 2 = U Q

alapján a

v = \sqrt[]{2 U Q / m}

. A Lorentz-erő figyelembevételével

\begin{matrix} \frac{m v^{2}}{r} = B v Q . \end{matrix}

Innen a szükséges mágneses indukció:

\begin{matrix} B = \frac{m v}{r Q} . \end{matrix}

Felhasználva a sugár geometriai kifejezését és a sebesség értékét:

\begin{matrix} B = \frac{2 sin α}{d} \sqrt[]{\frac{2 U m}{Q}} . \end{matrix}

Számadatainkkal

B = 0, 0037 tesla

b) Ebben az esetben az elektronágyúból kirepülő elektron sebességét felbontjuk a

B

mágneses indukció irányába eső

v cos α

és az erre merőleges

v sin α

összetevőre (5. ábra).

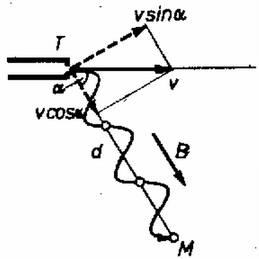5. ábra

v cos α

összetevőre hatástalan a mágneses tér. Ezzel a sebességgel az elektron

d / (v cos α)

idő alatt ér el az

M

célba.
Vizsgáljuk a mozgást olyan koordináta-rendszerből, amely

v \cdot cos α

sebességgel halad a

T M

irányban. Az elektron ebben a koordináta-rendszerben

v \cdot sin α

sebességgel körpályán mozog, amelynek sugara

m v^{2} sin^{2} α / r = B Q v sin α

alapján

\begin{matrix} r = m v sin α / (Q B) . \end{matrix}

(Az elektron valójában spirálist ír le.)

M

eltalálása akkor sikerül, ha az elektron

k

egész számú kört ír le az

M

-be való érkezés

d / (v cos α)

ideje alatt. A kör kerülete

2 π r = 2 π m v sin α / (Q B)

, egy körülfordulás ideje, tekintettel a körön való futás

v sin α

sebességére:

\begin{matrix} \frac{2 π m v sin α}{Q B v sin α} = \frac{2 π m}{Q B} . \end{matrix}

Ennek egész számú többszöröse

d / (v cos α)

\begin{matrix} \frac{d}{v cos α} = k \cdot \frac{2 π m}{Q B} . \end{matrix}

Innen a szükséges mágneses indukció:

\begin{matrix} B = k \cdot \frac{2 π m cos α}{d Q} \cdot v = k \cdot \frac{2 π cos α}{d} \sqrt[]{\frac{2 U m}{Q}} . \end{matrix}

Lényegtelen, hogy a mágneses indukció az adott irányban előre vagy hátra mutat, ettől csak a spirális menetiránya függ.

k = 1

esetében a spirális

1

menetével,

k = 2

-nél

2

-vel érjük el a célt stb. Számadatainkkal:

B = k \cdot 0, 0067 tesla

Kísérleti feladat. Adva van egy fekete doboz

A

B

C

egyforma csatlakozásokkal, benne csillagkapcsolásban

R

ellenállás és

C_{1}

C_{2}

kapacitású kondenzátorok vannak (6. ábra). Megállapítandó az ellenállás és a kapacitások nagysága!
Rendelkezésre áll egy generátor, amely

0, 1 kHz

és

10 kHz

között ismert frekvenciájú váltófeszültséget ad, azonkívül egy-egy váltóáramú ampermérő és voltmérő. Ezekkel az egyes dugók között lemérhetjük a feszültséget és áramerősséget, így megtudhatjuk az impedanciát és megvizsgálhatjuk az impedanciának a frekvenciától való függését.

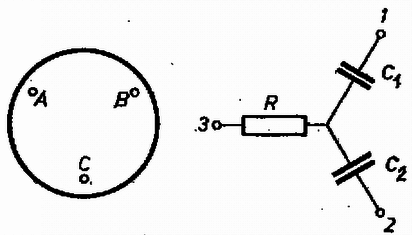6. ábra

Megoldás. Először meg kell tudni, a dugók közül melyik az, amelyikhez az ellenállás csatlakozik. A másik két dugó között tiszta (eredő) kapacitás található, amelyre nézve az impedancia és frekvencia fordítottan arányos. Tehát egy-egy impedanciamérést végzünk

0, 1 kHz

-nél és

10 kHz

-nél, és amelyik dugópár esetében az impedancia és a frekvencia fordítottan arányos, azokhoz vezetnek a kondenzátorok (legyenek ezek az

1

és

2

csatlakozások). Ezután többféleképpen dolgozhatunk tovább.
a) Egy bizonyos frekvenciánál lemérjük az

1

és

2

kivezetések között a sorba kapcsolt kondenzátorok eredő impedanciáját:

\begin{matrix} Z = \frac{1}{ω C_{1}} + \frac{1}{ω C_{2}} . \end{matrix}

(1)

Ezután lemérjük

1 - 3

, valamint

2 - 3

között az ellenállás és kondenzátor eredő impedanciáját:

Z_{1}

-et és

Z_{2}

-t, amelyekre

\begin{matrix} Z_{1}^{2} = R^{2} + {(\frac{1}{ω C_{1}})}^{2}, & (2) \\ Z_{2}^{2} = R^{2} + {(\frac{1}{ω C_{2}})}^{2} . & (3) \end{matrix}

Egyenletrendszert kaptunk

R

C_{1}

C_{2}

-re. Ebből a kapacitások:

\begin{matrix} \frac{1}{C_{1}} = \frac{ω}{2 Z} (Z^{2} + Z_{1}^{2} - Z_{2}^{2}), \\ \frac{1}{C_{2}} = \frac{ω}{2 Z} (Z^{2} - Z_{1}^{2} + Z_{2}^{2}) . \end{matrix}

Ismerve

C_{1}

és

C_{2}

nagyságát (2) vagy (3) könnyen megadja az

R

ellenállást.

b) Az

1

és

2

kivezetéseket összekapcsoljuk (a kapacitások most összegeződnek), azután két különböző frekvenciánál mérjük le az impedanciát

3

és az egyesített 1 ‐ 2 között:

\begin{matrix} Z_{a}^{2} = R^{2} + \frac{1}{ω_{a}^{2} {(C_{1} + C_{2})}^{2}}, \\ Z_{b}^{2} = R^{2} + \frac{1}{ω_{b}^{2} {(C_{1} + C_{2})}^{2}} . \end{matrix}

Az egyenletrendszerből

C_{1} + C_{2}

kapacitásösszeget kiküszöbölve kapjuk az ellenállásra:

\begin{matrix} R^{2} = \frac{ω_{a}^{2} Z_{a}^{2} - ω_{b}^{2} Z_{b}^{2}}{ω_{a}^{2} - ω_{b}^{2}} . \end{matrix}

R

ismeretében a (2) és (3) egyenletekkel számíthatók a kapacitások.

c) Ha elegendően kicsiny frekvenciával mérünk, akkor

R

elhanyagolható

1 / ω C_{1}

, illetve

1 / ω C_{2}

mellett és az impedanciákból rögtön számolhatjuk

C_{1}

-et és

C_{2}

-t. Ezután igen nagy frekvenciával mérve a kondenzátorok ellenállása hanyagolható el és az

R

ellenállást kapjuk meg.

d) Ha felrajzoljuk az 1 ‐ 3 és 2 ‐ 3 közötti impedanciáknak a frekvenciától való függését, akkor a frekvenciát növelve mindkét görbe közös aszimptotája adja meg az

R

ellenállást. Ennek ismeretében a (2) és (3) egyenletekből megkaphatók a kapacitások.