| Cím: | 1977. évi fizika OKTV feladatai | ||
| Füzet: | 1977/október, 81. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | OKTV | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1977. évi középiskolai tanulmányi verseny feladatai Az I. forduló feladatai 1. Teherautón tömegű, alapszélessegű, magasságú láda áll és a magasságú hátlaphoz támaszkodik . Mekkora gyorsulással indulhat az autó, hogy a láda le ne billenjen, ha a láda és az alap között nincs súrlódás, ha a láda és az alap között a súrlódási együttható ? A hátlap és a láda között nincs súrlódás. Számadatok: , , , , . 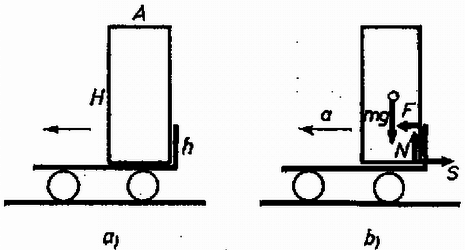 1. ábra Továbbá a határesetben 2. Ugyanazon anyagból, ugyanazon vastagságban készült kettős állócsiga sugarai és hosszúak, az állócsiga teljes tömege . A fonalakon -os tömegek lógnak . Elengedve a szerkezetet, a testek mennyi idő múlva jutnak rel mélyebbre? Megoldás. A csiga gyorsuló forgást végez. A sugarak arányából következik, hogy a kis csigának , a nagy csigának a tömege; így a kettőscsiga tehetetlenségi nyomatéka : 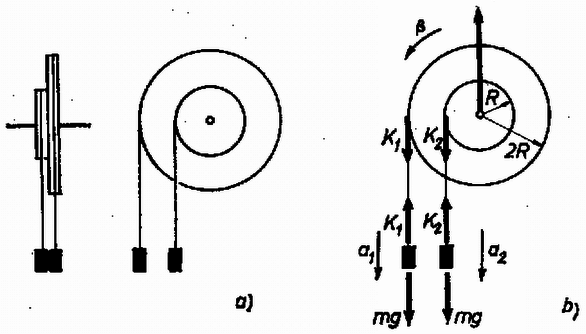 2. ábra Az elrendezésben szereplő három testre ható erők a 2.b) ábrán láthatók; , és a fonálerők. A gyorsulások és a szöggyorsulás jelölését, valamint a pozitív irányokat szintén az ábrán adtuk meg. A mozgásegyenlet a két tömegű testre:
Ennek az egyenletrendszernek a megoldása már valóságos eredményt ad: valamint 3. Egy hosszú, vékony üvegcső vízszintesen fekszik, benne hosszú légoszlopokat hosszú higanyoszlopok választanak el .a) ábra. Meddig lehet a cső nyitott végét lesüllyeszteni anélkül, hogy higany folyjék ki a csőből? Megoldás. A cső helyzetét az szög határozza meg [3.b) ábra]. 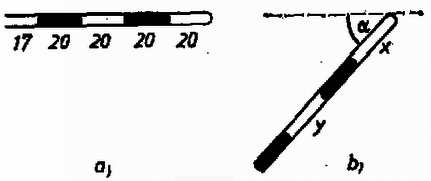 3. ábra A ferde csőben levő hosszúságú higanyszál két oldalán a légnyomáskülönbség: Megoldás. Először megállapítjuk, hogy a hasáb nem úszik, mert összsúlya , a kiszorított víz súlya . Megvizsgáljuk, a művelet folyamán mekkora darabbal kell feljebb emelni az egész berendezés súlypontját, vagyis mennyi a helyzeti energia változása. 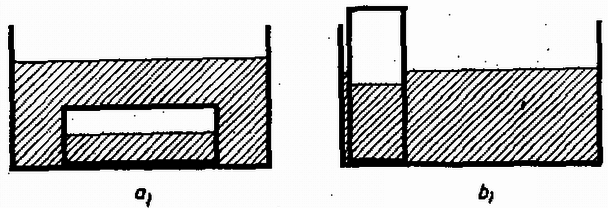 4. ábra Eredetileg a helyzeti energia, a nyitott edény aljához viszonyítva: A II. forduló feladatai 1. Homogén, tömör félgömböt peremének egy pontjában fonállal felfüggesztünk egy vízszintes, érdes asztallap fölött úgy, hogy éppen érintkeznek, de nem nyomják egymást (5. ábra). Ezután a fonalat elégetjük. Legalább mekkora legyen a súrlódási együttható, hogy a félgömb ne csússzék meg? A félgömb súlypontja a sugár -ában van. (Holics László) 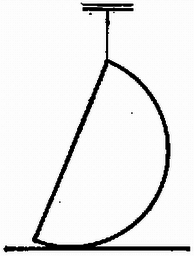 5. ábra Megoldás. A félgömb a fonál elégetésének pillanatában gyorsulva kezd mozogni. Legyen a tömegközéppont gyorsulásának vízszintes összetevője , függőleges összetevője , szöggyorsulása pedig (6. ábra). 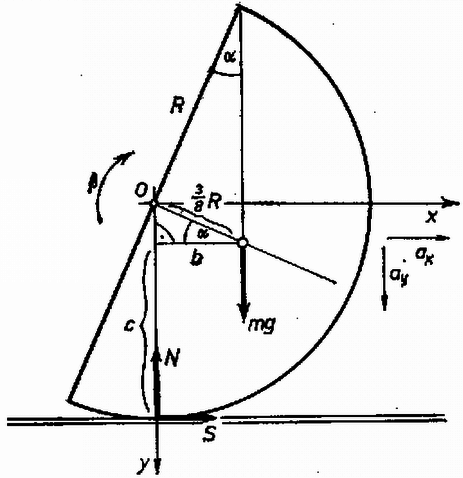 6. ábra Az elégetés után a félgömbre a következő erők hatnak: súlyerő (); súrlódási erő () és nyomóerő () az alátámasztási pontban. A mozgásegyenleteket az erők vízszintes és függőleges komponenseire, valamint a tömegközéppontra vonatkoztatott forgatónyomatékokra írjuk fel:
(Vermes Miklós) 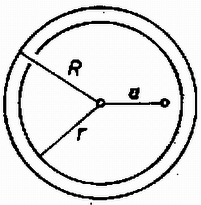 7. ábra Megoldás. Az üveg ‐ levegő határfelületre érvényes teljes visszaverődés határszöge határozza meg azt a nyílásszögű kettőskúpot, amelynek belsejéből minden fénysugár kijut a rendszerből (8. ábra). Ha ugyanis egy fénysugár a felületre érve részben megtörik (áthalad a felületen), részben visszaverődik, a gömb szimmetriája miatt a visszavert rész ismét azonos szögben éri el a gömb felületet, és egy része ismét kilép a rendszerből. Előbb-utóbb így minden, eredetileg a nyílásszögű kettőskúp belsejéből indult fénysugár kijut a rendszerből. 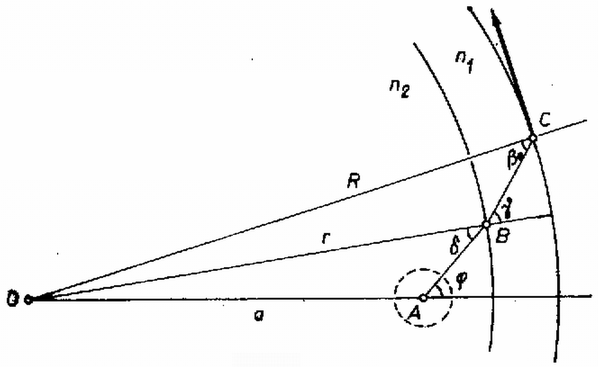 8. ábra A pontban (8. ábra) a teljes visszaverődés határszögére egyenlet teljesül. Az ehhez tartozó szöget az háromszögre felírt sinustétel adja: A kijutó fénymennyiség százalékának megállapítása érdekében a fényforrást egy sugarú gömbbel kell körülvenni, azután megállapítani, hogy kétoldalt a kilépő sugarakhoz tartozó gömbsüveg-felszín mekkora törtrésze az egész gömbfelületnek. A gömbsüvegek együttes felszíne , az egész gömbfelszín . Tehát a kijutó fény aránya: 3. Egy vákuumcsőben az izzószálból kilépő elektronok nyílásszögű nyalábban hagyják el az gyorsító feszültségű anódot (9. ábra). Útjukba állítunk egy fémháló-párt, amelynek hálói között potenciálkülönbség van. Mekkora legyen ez a potenciálkülönbség, hogy a nyaláb nyílásszögűvé terüljön szét? Számadatok: , . (Wiedemann László) 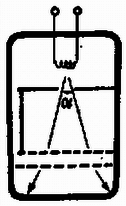 9. ábra Megoldás. A szélső elektronok sebességgel, a középvonalhoz képest szöggel lépnek át a felső hálón (10. ábra, az elektron töltése, pedig a tömege). 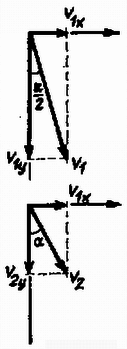 10. ábra A , sebesség vízszintes összetevője, , változatlanul megmarad, viszont a összetevő úgy csökken, hogy az szögből lesz. A szög kétszereződéséhez tartozó összefüggések: A III. kísérleti forduló a) Fektessen az asztalra papírlapot és erre indigót. Állványba fogott ferde csövön keresztül ejtsen az asztalon levő lapra acélgolyót. A pattogó golyó nyomot hagy a papíron. Mit és hogyan lehet megállapítani a papíron kapott pontsorból? b) Az asztalon található a ,,Cartesius-búvár'' néven ismert kísérleti eszköz, valamint egy üres kémcső, amely pontosan megegyezik a mérőhengerben levővel, tömege . A mérőhengerben levő folyadék mely anyagi állandóit tudná meghatározni az asztalon levő eszközök segítségével? c) Az asztalon található egy telep, egy ismeretlen ellenállás és egy feszültségmérő műszer. Mérések alapján határozza meg az ismeretlen ellenállás értékét! Az 1977. évi fizikai tanulmányi verseny eredménye. A fizikából nem tagozatos tanulók versenyében: A további helyezettek: 4. Dőry István (Budapest, Piarista Gimn. IV. o. t., Havas József), 5. Bozi Ferenc (Szombathely, Nagy Lajos Gimn. IV. o. t., Horváth István), 6. Rapai Tibor (Budapest, József Attila Gimn. IV. o. t., Honfi Lászlóné), 7. Gajdócsi Sándor (Bácsalmás, Hunyadi János Gimn. IV. o. t., Németh Mihály), 8. Váradi Ferenc (Miskolc, Földes Ferenc Gimn. IV. o. t., Dolák Gabriella), 9. Szigeti Antal (Kecskemét, Katona József Gimn. IV. o. t., Fodor István), 10. Köteles Zoltán (Budapest, I.László Gimn. IV. o. t., Szabó József). A fizikából tagozatos tanulók versenyében: A további helyezettek: 4. Ari Sándor (Ózd, József Attila Gimn. IV. o. t., Farkas Gézáné), 5. Kertay Zoltán (Budapest, Petőfi Sándor Gimn. IV. o. t., Iványi Tibor), 6. Kovács Zsolt (Szolnok, Verseghy Ferenc Gimn. IV. o. t., Sebestyén István), 7. Németh Gábor (Budapest, József Attila Gimn. III. o. t., Tóth Eszter), 8. Gráf István (Budapest, Petőfi Sándor Gimn. IV. o. t., Iványi Tibor), 9. Mari László (Nagykőrös, Arany János Gimn. IV. o. t., Mester Szabó József), 10. Bátori Péter (Bonyhád, Petőfi Sándor Gimn. IV. o. t., Katz Sándor). |