Kezdőlap


Cím:	1976. évi Eötvös Loránd Fizikaverseny
Füzet:	1977/február, 81. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1976. november 13-án rendezte 53. versenyét Budapesten és 8 vidéki városban idén érettségizettek és középiskolai tanulók részére. A versenyzők 5 órai munkaidő alatt oldhatták meg a három feladatot és bármilyen segédeszközt használhattak. A versenyzők száma 394 volt. Ismertetjük a feladatokat és megoldásukat.

M = 1000 kg

tömegű gépkocsi egyenletes körmozgást végez

R = 15 m

sugarú körpályán

ω = 0, 4 s^{- 1}

szögsebességgel. A gépkocsi

15 m

hosszú kötéllel

m = 200 kg

tömegű ládát vontat, amely szintén egyenletes körmozgást végez. A láda csúszó súrlódási együtthatója

0, 24

. Legyen a nehézségi gyorsulás

g = 10 {m/s}^{2}

.
a) Mekkora erő feszíti a kötelet ?
b) A talaj mekkora erővel hat a gépkocsira (a vízszintes síkban) ?
c) Mekkora a láda vontatására fordított teljesítmény ?
d) Vizsgáljuk meg a mozgást, ha

ω = 0, 2 s^{- 1}

(Vermes Miklós)

Megoldás A kötél hossza egyenlő az autó pályasugarával, így az 1. ábra alapján

\begin{matrix} cos φ = r / (2 R) . \end{matrix}

(1)

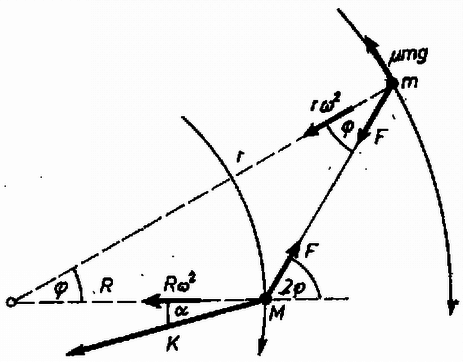1. ábra

A ládára a vízszintes síkban

μ m g

súrlódási erő hat az

r

sugarú körpálya érintője mentén, valamint az

F

kötélerő. A láda gyorsulása a kör középpontja felé mutat, nagysága

ω^{2} r

. A mozgásegyenletek a sugárirányú és az erre merőleges komponensekre:

\begin{matrix} m r ω^{2} = F \cdot cos φ, & (2) \\ 0 = F \cdot sin φ - μ m g . & (3) \end{matrix}

A gépkocsira a kötélerő, valamint a

K

súrlódási erő hat a vízszintes síkban. A mozgásegyenletek a sugárirányú és az erre merőleges komponensekre:

\begin{matrix} M R ω^{2} = K \cdot cos α - F \cdot cos 2 φ, & (4) \\ 0 = K \cdot sin α - F \cdot sin 2 φ . & (5) \end{matrix}

a) Az (1) és (2} egyenletekből kifejezhetjük a kötélerőt

\begin{matrix} F = 2 m R ω^{2} = 960 newton . \end{matrix}

b) (3)-ból

\begin{matrix} sin φ = μ m g / F = 0, 5, azaz φ = 30^{\circ}; \end{matrix}

(4)-ből és (5)-ből pedig

\begin{matrix} K = \sqrt[]{{(M R ω^{2} + F \cdot cos 2 φ)}^{2} + {(F \cdot sin 2 φ)}^{2}} = 2998 newton . \end{matrix}

c) A láda vontatásához szükséges teljesítmény a láda

ω r

sebességének és a

μ m g

vontató erőnek a szorzata:

\begin{matrix} P = ω r \cdot μ m g = 10, 392 \frac{m}{s} \cdot 480 newton = 4988 watt. \end{matrix}

d) A

sin φ = μ g / (2 ω^{2} R)

összefüggésből következik, hogy

ω = \sqrt[]{μ g / (2 R)} = 0, 28 s^{- 1}

esetében

φ = 90^{\circ}

és a láda a középpontba kerül. (Ez érvényes az ennél kisebb szögsebességekre is. Ilyenkor az

M ω^{2} R

erő megoszlása a kötélben ható és a talaj részéről működő erő között határozatlan.)

2. Bizonyítsuk be, hogy egy csillagászati távcsővel nézve ugyanolyan fényesnek látjuk a Holdat, mint szabad szemmel nézve, feltéve, hogy a két gyűjtőlencse átmérője elég nagy és az elnyelési veszteségektől eltekintünk !

Megoldás. Szabad szemmel nézve a Holdat, a széléről érkező párhuzamos sugárnyaláb az ideghártyán

A

-ban, a Hold középpontjáról érkező, szaggatottan jelzett nyaláb az ideghártyán

B

-ben gyűlik össze. A Holdról érkező és a szembe bejutó összes fény

A B

sugarú körön oszlik szét. Az érzékelt fényerősséget az jelenti, hogy a terület egységére mennyi fény jut (2. ábra).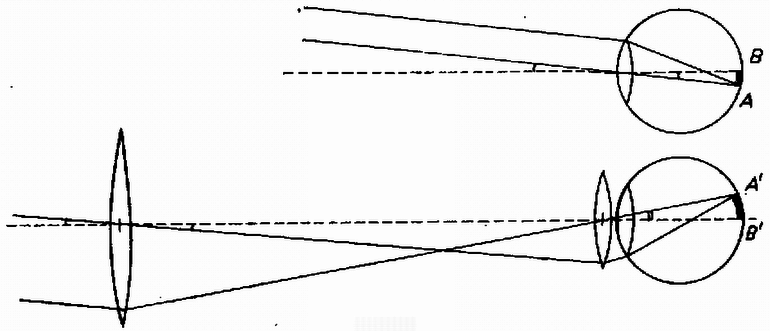

2. ábra

A csillagászati távcső

k

szögnagyítását a két lencse fókusztávolságának a hányadosa adja meg. A csillagászati távcsőn végezve a megfigyelést a Hold szélének a képe

A'

-ben, közepének a képe

B'

-ben keletkezik. A szembe ugyanolyan vastag sugárnyaláb kerül be, mint előbb, de ez a távcsőbe való belépéskor

k

-szor nagyobb átmérőjű volt, tehát a szembe

k^{2}

-szer több energia jut be. Azonban a

k

-szoros szögnagyítás folytán

A' B' = k \cdot A B

, az ideghártyán megvilágított kör területe

k^{2}

-szer nagyobb, mint előbb. Így a területegységre jutó fényenergia az előbbi, az érzékelt megvilágítási erősség változatlan.
A csillagászati távcső ún. teleszkópikus rendszer, a párhuzamos sugarakból álló nyaláb ugyancsak párhuzamos nyalábként lép ki, de

k

-szor nagyobb szögben és

k

-szor vékonyabban. Gondolatmenetünk akkor helyes, ha a lencsék átmérője elég nagy. A szemlencsének kb. akkorának kell lennie, mint a szem pupillájának, hogy ezen ne maradjon kihasználatlan terület, de ennél nagyobb szükségtelen, mert a pupilla mellé érkező fénysugarak fölöslegesek. A tárgylencse átmérőjének legalább a szemlencseátmérő

k

-szorosának kell lennie, hogy a szemlencse tele legyen fénnyel. Nagy nagyítás esetében ezt a feltételt nem lehet teljesíteni, és ekkor távcsővel kisebb megvilágítási erősséget látunk, mint szabad szemmel. A lencsék üveganyagának fényelnyelése ugyanerre vezet.
Mindez ún. felületi fényforrásokra vonatkozik. A pontszerű fényforrások geometriai optikával számított képe kisebb, mint egyetlen csap helye az ideghártyán, vagy mint egy ezüstbromid-szemcse a fényképezőlemezen. Ilyenkor a beérkezett fény összes mennyisége számít. Pontszerű fényforrás esetében legyen a tárgylencse (tükör) átmérője minél nagyobb, hogy minél több fény érkezzék az érzékelés helyére, ahol kisebb-nagyobb foltot kapunk, tekintettel a lencsehibákra stb. Pontszerű fényforrások a csillagok, sokszor a kisbolygók és kis-holdak, igen távoli ködfoltok.

3. Két egyforma, semleges fémgömb egyikének közelében a 3. ábrán látható módon földelt fémtű van. A két gömb között középen, felülről lassan leengedünk egy elektromosan töltött gömböt. Hol üt át először szikra ?

(Károlyházy Frigyes)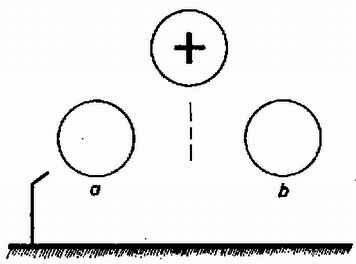

3. ábra

Megoldás. A csúcshatás következtében az

a

-gömbről a megosztott töltés egy része eltávozik szikrakisülés nélkül. Ezért az

a

-gömb alacsonyabb potenciálon van, mint a

b

-gömb. A töltött gömb és a föld között bármely úton haladva ugyanannyi a potenciálkülönbség, azonban ebből

a

és a töltött gömb közötti részre több jut, mint a töltött gömb és

b

közötti részre, tehát a szikra először a töltött gömb és

a

között csap át.

A verseny eredménye

I. díjat nyert Vankó Péter (Bp. Móricz Zsigmond Gimn. IV. o. t., tanára Sikó Attiláné). II. díjat nyertek Kárpáti Tibor honvéd (érettségizett Pécsett a Zipernovszky K. Szakközépiskolában mint Balogh József tanítványa) és Surány Gábor (Bp. I. István Gimn. IV. o. t., tanára Cseh Géza). III. díjat nyertek Hanula Barna (Bp. Berzsenyi Dániel Gimn. IV. o. t., tanára Hubert Györgyné), Sebestyén György (Bp. I. István Gimn. IV. o. t., tanára Cseh Géza) és Tankovits Tibor (Bp. Kaffka Margit Gimn. IV. o. t., tanára Mórocz Béláné). Dicséretet kaptak jutalommal: Biegl Csaba (Bp. József Attila Gimn. IV. o. t., tanára Bakányi Márton), Hujter Mihály, az ELTE matematikus hallgatója (érettségizett Pápán a Türr István gimnáziumban mint Varga Gyula tanítványa), Kriza György (Bp, Fazekas Mihály Gimn. III. o. t., tanárai Szalay Béla és Tóth László) és Rapai Tibor (Bp. József Attila Gimn. IV. o. t., tanára Honfi Lászlóné).