Cím:	A termodinamika alapjai
Szerző(k):	Mihály László
Füzet:	1977/január, 33 - 42. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A termodinamika alapjai${}^{*}$   A természeti folyamatok leírására különböző törvényeket állíthatunk fel, amelyek segítségével megjósolhatók a törvények érvényességi körébe tartozó események. Szép példa erre a klasszikus mechanika, ahol már középiskolás szinten is matematikai tisztasággal tanulmányozható az alaptörvények mechanizmusa. Általános probléma azonban, hogy a folyamatokban résztvevő egységek számát növelve a matematikai nehézségek rohamosan növekszenek, és hamarosan a numerikus módszerek is csődöt mondanak. A klasszikus mechanikában bizonyított tétel például, hogy már három, egymással gravitációs kölcsönhatásban álló test mozgásegyenleteinek megoldása sem adható meg zárt formában. A kvantummechanikai többtestprobléma (pl. a hidrogénnél nehezebb atomok elektronszerkezetének megadása) szintén csak közelítőleg oldható meg. Még a legnagyobb számítógépek is ‐ amelyekkel egyes kristályszerkezetekben lezajló folyamatokat szimulálnak ‐ csak kb. 1000 atom szimultán mozgását tudják követni. Érdekes tény viszont, hogy ha egy rendszerben nagyon sok egyforma részecske van, akkor ismét találhatunk általános törvényszerűségeket, amelyek ugyan nem adják meg az egyes részecskék helyzetét és sebességét (a rendszer mikroszkopikus állapotát), de sok, számunkra érdekes kérdésre választ adnak. A fenomenologikus termodinamika tapasztalati tények alapján felállított kis számú axómia és a folyamatokban résztvevő anyagok ugyancsak tapasztalatból ismert állapotegyenlete segítségével meghatározza a rendszer makroszkopikus állapotát. A statisztikus fizika egyszerű alapfeltevésekből, pusztán a részecskék nagy számát és egyformaságát feltételezve bebizonyítja a termodinamika alaptörvényeit, és képes arra, hogy az egyes részecskék közötti mikroszkopikus kölcsönhatásból meghatározza az anyag állapotegyenletét. Az alábbiakban a fenomenologikus termodinamika alapjaival ismerkedünk meg, és a fogalmak megértéséhez szükséges szemléletes mikroszkopikus képet kaphatunk.   I. A termodinamika tárgya. Állapotjelzők   A termodinamika egy rendszer jellemzésére úgynevezett állapotjelzőket használ, amelyek közös vonása, hogy a rendszer makroszkopikus tulajdonságait írják le. (Nem állapotjelző pl. a rendszert alkotó részecskék térbeli helyzete; állapotjelző a rendszer térfogata, ami bizonyos értelemben az előbbi mennyiség átlagolásával kapható.) Állapotjelző csak olyan mennyiség lehet, amely független attól, hogy a rendszer egy korábbi állapotából milyen úton jutott az új állapotba. (Egy dugattyús hengerbe zárt gáz állapotjelzője lehet a dugattyú pillanatnyi távolsága a henger szemközti falától, de nem állapotjelző pl. a dugattyú által megtett út ‐ azaz az elmozdulások abszolút értékeinek összege.) 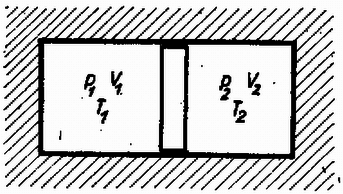    1. ábra   A termodinamika mindig energiacserével kapcsolatos jelenségeket tárgyal, ezért állapotjelzőnek csak azokat a paramétereket nevezzük, amelyek az energiacserével kapcsolatosak. Ez a kapcsolat mindig $\begin{array}{c}{\displaystyle \Delta E=x\cdot \Delta Y}\end{array}$ alakú, ahol $\Delta E$ a rendszer energiájának változása, $x$ egy állapotjelző, $\Delta Y$ pedig egy másik állapotjelző megváltozása. Az állapotjelzőket tehát két csoportra oszthatjuk aszerint, hogy az energiacsere nagyságát pillanatnyi értékük ($x$, intenzív állapotjelző), vagy pedig megváltozásuk ($Y$, extenzív állapotjelző) határozza meg. Néhány példát az alábbi táblázatban közlünk.   ${\displaystyle \begin{array}{|ccccccc|}\hline \hfill {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle \text{Intenzív}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mi>p</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>α</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>U</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>μ</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>T</mi></math>}}\hfill \\ \hfill {\displaystyle }\hfill & {\displaystyle \text{nyomás}}\hfill & {\displaystyle \text{felületi}}\hfill & {\displaystyle \text{erő}}\hfill & {\displaystyle \text{feszültség}}\hfill & {\displaystyle \text{kémiai}}\hfill & {\displaystyle \text{hőmérséklet}}\hfill \\ \hfill {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle \text{feszültség}}\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle \text{potenciál}}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle \text{Extenzív}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>V</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>l</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>q</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>N</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>S</mi></math>}}\hfill \\ \hfill {\displaystyle }\hfill & {\displaystyle \text{térfogat}}\hfill & {\displaystyle \text{felület}}\hfill & {\displaystyle \text{hosszú-}}\hfill & {\displaystyle \text{töltés}}\hfill & {\displaystyle \text{részecske-}}\hfill & {\displaystyle \text{entrópia}}\hfill \\ \hfill {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle \text{ság}}\hfill & {\displaystyle }\hfill & {\displaystyle \text{szám}}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle \text{Munka-}}\hfill & {\displaystyle \text{térfogati}}\hfill & {\displaystyle \text{felületi}}\hfill & {\displaystyle \text{rugalmas}}\hfill & {\displaystyle \text{elektromos}}\hfill & {\displaystyle \text{kémiai}}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle \text{végzés}}\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill & {\displaystyle }\hfill \\ \hline\end{array}}$   Látható, hogy az állapotjelzők az utolsó kettő ($S\mathrm{,}T$) kivételével a fizika más ágaiból ismert, jól definiált mennyiségek. ($\Delta W=\mu \cdot \Delta N$ ún. kémiai munkavégzés akkor történik, ha a rendszer részecskeszáma megváltozik, pl. kémiai reakciókban. Ilyenkor a részecskékbe korábban bezárt energia egy része szabadul fel, és növeli a rendszer energiáját.) Tapasztalat, hogy egy rendszer állapotának teljes jellemzéséhez kis számú, de minimálisan három állapotjelző (pl. nyomás, energia, térfogat) elegendő, és ezeket ki lehet úgy választani, hogy definíciójuk és mérési utasításuk a fizika más ágaiból ismert legyen. Az extenzív és intenzív állapotjelzők egy másik, ekvivalens definíciója: Ha egy egyensúlyban levő rendszert képzeletben két azonos részre osztunk, akkor az extenzív állapotjelzők (pl. térfogat) feleződnek, az intenzívek (pl. nyomás) pedig változatlanok maradnak. Az alábbiakban a termodinamikának azzal a részével foglalkozunk, amelynek célja egy zárt rendszer új egyensúlyi állapotának megkeresése, ha az eddigiekben tiltott energiacserélési formák közül néhányat megengedünk. (Zárt a rendszer, ha környezetével nem cserél energiát; egyensúlyban van, ha állapotjelzői nem változnak.) Az alapfeladat tehát olyan jellegű, mint az 1. ábrán látható példa: mi lesz az új egyensúlyi állapot, ha a falat hővezetővé tesszük? A probléma megoldása során bevezetett fogalmak később egyszerűen elvezetnek olyan mennyiségekhez is, mint a hőkapacitás, a hőtágulási együttható stb. Az utóbbi évtizedekben kifejlődött a termodinamikának egy olyan ága (az ún. irreverzibilis termodinamika), amely nemcsak a már beállt egyensúlyi állapotot képes megjósolni, hanem foglalkozik a folyamat időbeli lefolyásával is. Újabban már szokásos ezt az új, ún. irreverzibilis termodinamikát nevezni termodinamikának, míg a hagyományos termodinamikának (amellyel ez a cikk is foglalkozik) új nevet adtak; a termosztatikát. Várható, hogy a jövőben ezek az elnevezések válnak majd általánossá, mert a fizikai fogalmaknak valóban jobban megfelelnek. (Dr. Bodó Zalán)   II. A termodinamika módszerei   A fenti tárgykörben az anyag viselkedéséről szerzett ismereteinket a termodinamika főtételeibe sűrítettük. E tételek matematikai formába önthetők, és ezek képezik a továbbiakban mindig érvényes "játékszabályokat''. A rendszer állapotát maradéktalanul leíró állapotjelzők értékének függvényében a többi állapotjelző kifejezhető. Az állapotjelzők közötti kapcsolat a vizsgált rendszerre jellemző, és matematikai formája az állapotegyenlet. Az anyag állapotegyenleteit méréssel vagy elméleti úton a statisztikus fizika módszereivel határozhatjuk meg. A keresett megoldást általában a főtételek, az állapotegyenletek és a meghatározandó mennyiség definíciójának összevetésével kaphatjuk meg. A továbbiakban először ismertetjük a főtételeket, majd néhány anyag állapotegyenleteit. Végül feladatokat közlünk, amelyek megoldásával az új ismeretek elmélyíthetők.   III. Az első főtétel   Kísérleti tapasztalat, hogy ha mérjük egy makroszkopikus rendszer teljes energiájának megváltozását, és meghatározzuk a rendszeren végzett munkák összegét $\left(\Delta W=-p\cdot \Delta V+\alpha \cdot \Delta A+\text{...}\right)$, akkor általában $\Delta E\ne \Delta W$. Hogy az eddig általánosnak bizonyult energiamegmaradás törvényét fenntarthassuk, bevezetünk egy új energiacserélési formát, a hőközlést, amelynek nagyságát a $\begin{array}{c}{\displaystyle \Delta Q=\Delta E-\Delta W}\end{array}$ egyenlet definiálja. A termodinamika első főtétele tehát: $\begin{array}{c}{\displaystyle \Delta E=\Delta Q-p\cdot \Delta V+\alpha \cdot \Delta A+\text{...}\mathrm{.}}\end{array}$ (Általában a munkavégzések közül csak a legfontosabbat, a térfogati munkát írjuk ki.) A fenti axiómát az igazolja, hogy a belőle később levezetett összefüggések a tapasztalattal összevetve igaznak bizonyulnak. Ha valaki mégis magyarázatot igényel, akkor a termodinamika kereteiből kilépve a következő szemléletes mikroszkopikus kép adható. A rendszer részecskéinek mozgása két részre bontható: egy rendezett, kollektív mozgásra és az ettől való eltérésre. Normális méretekben csak az első figyelhető meg, pl. amikor egy rugó 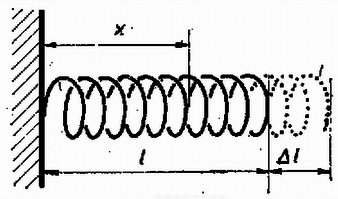$\Delta l$-lel megnyújtva az $x$ helyen található atomok $\Delta x=\left(\Delta l/l\right)\cdot x$ mértékben elmozdulnak (2. ábra).     2. ábra   Természetesen lehetséges olyan változás, amelynek során csak a rendezett mozgás módosul, és ezt a szokásos állapotjelzők $\left(V\mathrm{,}N\right)$ változása nem feltétlenül jelzi. Ekkor tehát a rendszer energiája változik, de szokásos munkavégzés nem történik; ez a hőközlés. A hőközlés mint energiacserélési forma létezése tehát a termodinamikai szemléletmód alapjaiból következik, abból, hogy a rendszert átlagolt, makroszkopikus mennyiségekkel akarjuk leírni. Fontos megjegyezni, hogy mivel a rendszer energiája állapotjelző, de a rendszeren végzett munka nem az (mert ugyanabba az állapotba különböző módon eljutva a végzett munka más és más lehet), a hőcsere sem állapotjelző, hanem a munkavégzéssel analóg fogalom. Ezért nincs értelme egy testben található "hőmennyiségről'' beszélni. (Ugyanúgy, mint ahogy nem beszélünk a testben levő munka mennyiségéről sem.)   IV. A második főtétel   Az első főtétel nem elégséges a rendszer egyensúlyi állapotának meghatározásához, másrészt megenged a tapasztalattal ellentmondó hőcserével kapcsolatos jelenségeket. Ezért további axiómák felállítása szükséges. Tapasztaljuk, hogy ha egy hőszigetelő fallal két részre osztott rendszerben a fal hőszigetelését megszüntetjük (pl. két vasdarabot összeérintünk), akkor általában energiaáramlás indul meg. Előre megmondhatjuk, hogy lesz-e energiacsere, ha mindkét részrendszerrel megfelelő módon azonos mennyiségű és minőségű gázt (gázhőmérőt) hozunk kapcsolatba, és összehasonlítjuk azok hőtágulását. A tágulás mértékét a vizsgált rendszer "melegségének'' (tapasztalati hőmérsékletnek) nevezzük. Azt, hogy erről a fogalomról egyáltalán beszélhetünk, hogy létezik, a termodinamika nulladik főtételének szokás nevezni. A második főtételnek több megfogalmazása van. Ezek közül az egyik: Hőközlés formájában történő energiacsere során a melegebb test energiája csökken, a hidegebbé nő. Ez szemléletes és egyszerű axiómia, de matematikailag nem kezelhető. Hasznosabb a másik, vele ekvivalens kijelentés: Létezik abszolút termodinamikai hőmérséklet $\left(T\right)$ intenzív és entrópia $\left(S\right)$ extenzív állapotjelző, melyekkel a hő formájában történő energiacsere $\begin{array}{c}{\displaystyle \Delta Q=T\cdot \Delta S}\end{array}$ alakban írható. Zárt rendszer entrópiája önmagától nem csökkenhet. Az utóbbi megfogalmazás kevésbé szemléletes, ezért az elsőből bizonyítjuk. A bizonyítás jellegzetesen termodinamikai gondolatmenet lesz, a valóságosaktól meglehetősen távoli fogalmakat használ, melyeket alább definiálunk. Hőtartálynak nevezzük azt a testet, melynek "melegsége'' akkor sem változik, ha hő formájában energiát ad le vagy vesz fel. Folyamat a test állapotában egymás után bekövetkező változások sorozata. Kvázisztatikus az a folyamat, melynél a vizsgált rendszer minden piIlanatban egyensúlyban van. Ezen azt kell érteni, hogy a változás ideje az egyensúly beálltához szükséges mikroszkopikus folyamatok időtartamához képest nagy. Nem kvázisztatikus folyamat pl. egy robbanás. A kvázisztatikus folyamat elképzelésére azért van szükség, hogy az állapotjelzők a folyamat egészére értelmezhetők legyenek. Reverzibilis az a kvázisztatikus folyamat, amelynek bármely pillanatában az állapotjelzők egész kis megváltoztatásával a folyamat ellenkező irányúvá tehető. Nem minden kvázisztatikus folyamat reverzibilis.   A reverzibilis folyamatok nagy szerepet játszhatnak egyes gondolatmenetekben, de kitüntetett voltuk nem jelenti azt, hogy a termodinamika nem érvényes, ha a folyamatok nem reverzibilisek. Egyszerűen arról van szó, hogy pl. egy gáztömeg robbanásszerű kiterjedésénél módszereinkkel csak a kezdeti és végállapot határozható meg, a közbenső állapotok nem.   További speciális folyamatok:   Izotermikus: az anyag "melegsége'' nem változik. Adiabatikus: a rendszer a folyamat során energiát hő formájában nem kap. Izobár: állandó nyomáson végbemenő folyamat. Izochor: állandó térfogaton végbemenő folyamat. Körfolyamat, amelynek végén az anyag visszajut eredeti állapotába. Carnot-körfolyamat: olyan reverzibilis körfolyamat, amely izotermikus és adiabatikus állapotváltozásokból áll. Első szakaszában a rendszer egy ${\tau }_1$ melegségű hőtartályhoz kapcsolva izotermikusan $Q_1$ energiát vesz fel. Utána egy adiabatikus folyamat során melegségét ${\tau }_2$ értékre változtatjuk, majd egy ${\tau }_2$ melegségű hőtartállyal kapcsolva $Q_2$ hőt ad le. Végül adiabatikus úton visszajut eredeti állapotába. A kvázisztatikus folyamatok ‐ így a Carnot-körfolyamat is ‐ nagyon jól szemléltethetők egy síkon, melynek minden pontja a rendszer egy állapotának felel meg. A kapott ábra természetesen függ attól, hogy a folyamatot milyen anyagon hajtjuk végre. 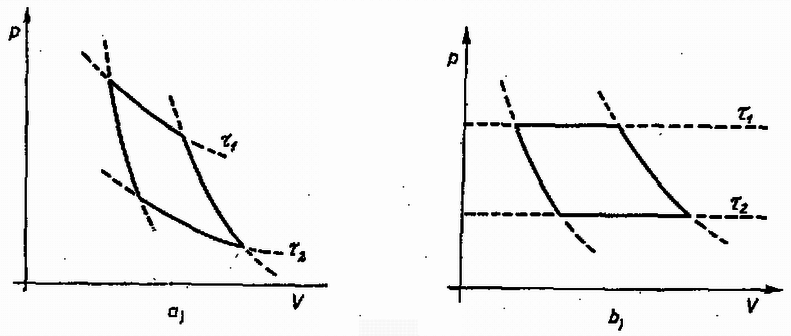    3. ábra   A 3. ábrán  feltüntettünk két Carnot-körfolyamatot a) ideális gázzal, b) fotongázzal. A görbék meghatározásánál az áIlapotegyenleteket használtuk fel, ezekről később lesz szó. Hatásfok. Ha a Carnot-körfolyamatot gázzal végezzük, akkor nyilvánvaló, hogy a körfolyamat végén munkát nyerhetünk, ha a gáz nagyobb melegségű (és nyomású) állapotban tágul és kisebb melegségű (és nyomású) állapotban nyomódik össze. Általában tetszőleges anyag esetén a hatásfok azt mutatja meg, hogy a körfolyamat során a hőközléssel felvett energia hányadrésze távozik mint mechanikai munka: $\begin{array}{c}{\displaystyle \eta =W/Q\mathrm{.}}\end{array}$ Az első főtétel szerint $\Delta E=0\text{(mert körfolyamat)}=Q_{\text{<span style="font-style: italic;">felvett</span>}}-Q_{\text{<span style="font-style: italic;">leadott</span>}}-W$, tehát $\begin{array}{c}{\displaystyle \eta =\frac{Q_f-Q_l}{Q_f}\mathrm{.}}\end{array}$ A fenti fogalmak felhasználásával először azt bizonyítjuk be, hogy minden Carnot-körfolyamat hatásfoka azonos, ha ${\tau }_1$ és ${\tau }_2$ adott. Természetesen a bizonyításhoz felhasználjuk a második főtétel előbbi egyszerű megfogalmazását. Vegyünk két Carnot-gépet (különböző anyagokkal töltve), melyeket egy nagyobb 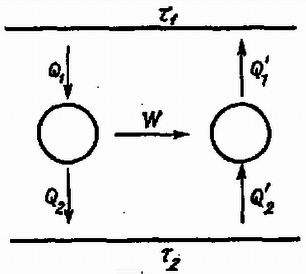$\left({\tau }_1\right)$ és egy kisebb $\left({\tau }_2\right)$ melegségű hőtartállyal hozhatunk kapcsolatba. A 4. ábrán berajzoltuk egy kör során létrejövő energiacseréket, figyelembe véve azt, hogy az egyik gép által termelt munkát teljes egészében arra használjuk, hogy a másik gépet mint "hőszivattyút'' üzemeltessük.     4. ábra   Az első főtételből következik, hogy $\begin{array}{c}{\displaystyle Q_1-Q_2=Q_1\text{'}-Q_2\text{'}\mathrm{.}}\end{array}$ (1) A második főtétel egyszerű megfogalmazásából következik, hogy a) ha a körfolyamat olyan irányú, hogy $Q_1$, $Q_1\text{'}$ pozitív, akkor $\begin{array}{c}{\displaystyle Q_1\text{'}-Q_1\le \mathrm{0,}}\end{array}$ mert a magasabb hőmérsékletű hőtartály nem vehet fel hőt; b) mivel a Carnot-körfolyamat reverzibilis, a folyamat ellenkező irányban is végbemehet. Ekkor valamennyi energiacsere előjelet vált, és a második főtétel miatt most $\begin{array}{c}{\displaystyle Q_1\text{'}-Q_1\ge 0.}\end{array}$ A két kikötés egyszerre csak akkor teljesülhet, ha $\begin{array}{c}{\displaystyle Q_1=Q_1\text{'}\mathrm{.}}\end{array}$ (2) (1), (2) és a hatásfok definíciójának felhasználásával könnyen belátható, hogy a két gép hatásfoka egyenlő. Ezt a tényt fogjuk felhasználni az abszolút hőmérséklet definiálására. Ha a Carnot-gép hatásfoka nem függ a belehelyezett anyagtól, akkor csak a hőtartályok termodinamikai állapotától függhet. Abszolút hőmérsékletnek nevezzük azt a mennyiséget, amelyet úgy kapunk, hogy a vizsgált testet és a hőmérséklet-etalon hőtartályt (a hőmérséklet méréséhez ugyanúgy kell etalon, mint a távolság vagy tömeg méréséhez) bármilyen Carnot-géppel összekötve, a körfolyamat hatásfokából képezzük a ${\displaystyle \begin{array}{c}\hfill {\displaystyle T=\left(1-\eta \right)\cdot T_E\mathrm{,}\text{ha}\tau <{\tau }_E}\hfill \\ \hfill {\displaystyle T=\frac{1}{1-\eta }{T}_E\mathrm{,}\text{ha}\tau >{\tau }_E}\hfill \end{array}}$ mennyiséget. ($T_E$ az etalon hőmérséklet. Ha pl. az etalon hőtartály olvadó jég, akkor $T_E=273\text{K}$ választással a Kelvin-féle hőmérsékleti skálát kapjuk.) A hőmérsékletnek ezen választása azért is kényelmes, mert ‐ mint az bizonyítható ‐ az ideális gáz állapotegyenletei ekkor $\begin{array}{c}{\displaystyle pV=N\cdot kT}\end{array}$ $\begin{array}{c}{\displaystyle E=a\cdot p\cdot V}\end{array}$ alakúak lesznek, és a hőmérsékleti skála egybeesik az ideális gázból készült gázhőmérőn egyenletes osztásokkal képzett skálával. A hőmérséklet ismeretében keressük meg a hozzá tartozó extenzív állapotjelzőt! Rendeljük a rendszer egy adott állapotához az $S_1$ mennyiséget! Bármely másik állapotba eljuthatunk adiabatikus és izotermikus állapotváltozások sorozatával. Legyen az $S$ mennyiség változása $\Delta S=0$ adiabatikus, $\Delta S=\Delta Q/T$ izotermikus folyamatnál.   Bizonyítjuk, hogy a fenti módon definiált mennyiség állapotjelző, azaz értéke független attól, hogy a rendszer milyen módon jut új állapotába. Ha először izotermikusan, azután adiabatikusan jutunk az új állapotba, akkor $\begin{array}{c}{\displaystyle S_2=S_1+Q_1/T_1\mathrm{.}}\end{array}$ Először adiabatikusan, utána izotermikusan haladva: $\begin{array}{c}{\displaystyle S_2\text{'}=S_1+Q_2/T_2\mathrm{.}}\end{array}$ A hőmérséklet definíciójából azonban következik, hogy $Q_1/T_1=Q_2/T_2$, tehát $S_2=S_2\text{'}$. Egyszerűen bizonyítható, hogy $S_1$ értékére egyéb úton haladva is ugyanazt kapjuk, ez a mennyiség tehát valóban állapotjelző, a neve: entrópia. A definícióból látható, hogy a hőközlés $\begin{array}{c}{\displaystyle \Delta Q=T\cdot \Delta S}\end{array}$ alakban írható. Így az első és második főtétel egyesített alakja: $\begin{array}{c}{\displaystyle \Delta E=T\cdot \Delta S-p\cdot \Delta V+\alpha \cdot \Delta A+\text{...}\mathrm{.}}\end{array}$ Az entrópia és a hőmérséklet tehát bizonyos értelemben rokon mennyiségek, mindkettő létezése a második főtételnek köszönhető. A különbség ‐ és a nehézség ‐ onnan származik, hogy az egyik értékelésére van érzékszervünk, a másikéra nincs. A második főtétel első megfogalmazásából és az entrópia definíciójából egyszerűen bizonyítható az entrópianövekedés tétele is. Említettük, hogy a hőközlés a mikroszkopikus képben a rendezetlen mozgásban bekövetkezett változással jár együtt. Másrészt láthattuk, hogy az entrópiaváltozás és a hőközlés között szigorú termodinamikai kapcsolat van. Ebből következik, hogy az entrópia valamilyen módon a mikrorészecskék rendezetlenségére jellemző szám. Az entrópianövekedés tétele egyszerűen azt fejezi ki, hogy a részecskék rendezetlen mozgása önmagától nem alakul rendezetté.   V. A harmadik főtétel   Az entrópia fenti definíciójában csak az entrópia változását rögzítettük le, az abszolút érték egy additív állandó erejéig határozatlan maradt. A harmadik főtétel az entrópiát egyértelművé teszi azzal, hogy kimondja: Minden rendszer entrópiája tart nullához, ha hőmérsékletével nullához tartunk. Az állítást azért kell ilyen óvatosan fogalmazni, mert ebből a tételből bizonyítható, hogy az anyagokat nem lehet $T=0$-ra hűteni. A gyakorlatban a harmadik főtételt ritkábban használjuk.   VI. Állapotegyenletek   Az ideális gáz állapotegyenleteivel már megismerkedtünk. További két egyszerű példa adható: Fotongáz: ${\displaystyle \begin{array}{c}\hfill {\displaystyle pV=\left(1/3\right)E}\hfill \\ \hfill {\displaystyle E=\left(\sigma /c\right)\cdot V\cdot T^4\mathrm{,}}\hfill \end{array}}$ ahol $\sigma$ a Stefan-Boltzmann állandó, $c$ a fénysebesség. Ez az egyenletrendszer az üregbe zárt elektromágneses hullámok viselkedését írja le. A reális gázokat jobban közelítő ún. van der Waals-féle gáz: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \left(p+N^{2}a/V^2\right)\cdot \left(V-Nb\right)=NkT\mathrm{,}}\hfill \\ \hfill {\displaystyle E=N\cdot c_V\cdot T-N^{2}a/V\mathrm{.}}\hfill \end{array}}$ Nagy hőmérsékleten, ha $V$ és $p$ nagy, a reális gáz az ideális gázhoz hasonlóan viselkedik. Az $a$ és $b$ állandó megválasztható úgy, hogy ez az egyenlet egy valódi gáz viselkedését alacsony hőmérsékleten is elég jól modellezze. Mikroszkopikus magyarázat: az $a$ állandó a molekulák közötti vonzó kölcsönhatást, a $b$ állandó a molekulák véges térfogatát veszi figyelembe. Az állapotegyenletek szintén szemléltethetők az állapotsíkon (5., 6. ábra). 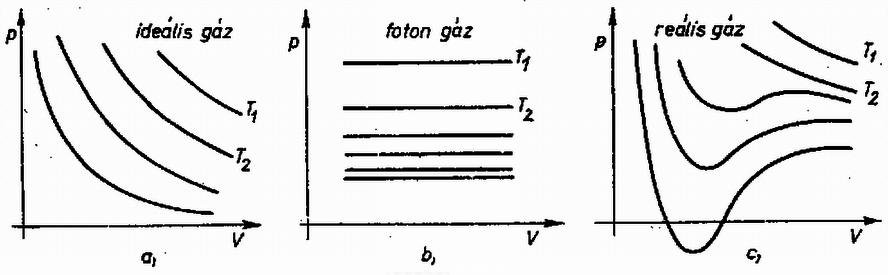    5. ábra 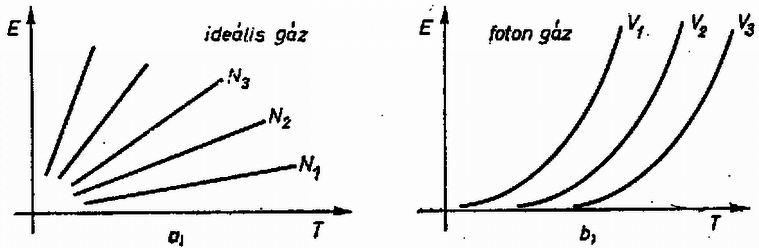      6. ábra   A főtételek felhasználásával az anyag állapotegyenletei egy egyenletbe foglalhatók össze. Ez az egyenlet ‐ az úgynevezett fundamentális egyenlet ‐ egyszerű esetben egy $\begin{array}{c}{\displaystyle S=f\left(E\mathrm{,}V\mathrm{,}N\right)}\end{array}$ alakú függvény, amelyből az állapotegyenletek differenciálással nyerhetők, miközben felhasználjuk az első és második főtétel egyesített alakját: $\begin{array}{c}{\displaystyle \Delta S=\left(1/T\right)\Delta E+\left(p/T\right)\Delta V\mathrm{.}}\end{array}$ Tehát ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\Delta S}{\Delta E}|{}_{\text{ha}{}_{\Delta V=0}}=\frac{1}{T}=\frac{\text{d}f\left(E\mathrm{,}V=\text{áll}\mathrm{.,}N=\text{áll}\mathrm{.}\right)}{\text{d}E}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\Delta S}{\Delta V}|{}_{\text{ha}{}_{\Delta E=0}}=\frac{p}{T}=\frac{\text{d}f\left(E\mathrm{,}V=\text{áll}\mathrm{.,}N=\text{áll}\mathrm{.}\right)}{\text{d}V}\mathrm{.}}\hfill \end{array}}$ A fenti tétel illusztrálására lássunk két példát! Ideális gáznál ($V_0$ és $E_0$ állandók): $\begin{array}{c}{\displaystyle S=k\cdot N\cdot \text{ln}\left(V/V_0\right)+akN\cdot \text{ln}\left(E/E_0\right)\mathrm{.}}\end{array}$ Ebből ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{1}{T}=\frac{\text{d}\left(kN\text{ln}\left(V/V_0\right)+ak\cdot N\cdot \text{ln}E/E_0\right)}{\text{d}E}=a\cdot k\cdot N\cdot \frac{1}{E}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{p}{T}=\frac{\text{d}\left(kN\text{ln}\left(V/V_0\right)+a\cdot k\cdot N\cdot \text{ln}E/E_0\right)}{\text{d}V}=k\cdot N\cdot \frac{1}{V}\mathrm{,}}\hfill \end{array}}$ ez pedig valóban a két állapotegyenlet átrendezett alakja. Fotongáznál: $\begin{array}{c}{\displaystyle S=\sqrt[4]{\frac{\sigma }{c}}\cdot \frac{4}{3}\sqrt[4]{{\left(\frac{E}{V}\right)}^3}\cdot V\mathrm{.}}\end{array}$ A számítás elvégzését az olvasóra bízzuk. Láthatjuk, hogy az entrópiafüggvény létezésének (vagyis tulajdonképpen a második főtételnek) az a következménye, hogy egy anyag állapotegyenletei nem teljesen függetlenek, mert ugyanannak a függvénynek különböző változó szerinti deriváltjai.   VII. Feladatok   Az első főtétel alkalmazása   1. Határozzuk meg az ideális gáz egy molekulájára fajhőjét, azaz a $\begin{array}{c}{\displaystyle c=\left(1/N\right)\cdot \Delta Q/\Delta T}\end{array}$ mennyiséget a) állandó térfogaton, b) állandó nyomáson, c) általában a $p\cdot V^{\alpha }=\text{áll}$. folyamatokban ($\alpha$ tetszőleges szám).   Megoldás. a) $c_V=a\cdot k$; ez az eredmény magyarázza, miért szokták az ideális gáz második állapotegyenletét $E=c_V\cdot N\cdot T$ alakban írni. b) $c_p=c_V+k$; c) $c=\frac{k}{1-\alpha }+c_V$; látható, hogy $\alpha =\frac{c_V+k}{c_V}$ esetén a fajhő nulla, azaz ekkor a gáz nem tud energiát felvenni hő formájában. Ezért az adiabata egyenlete: $\begin{array}{c}{\displaystyle p\cdot V^{\frac{c_V+k}{c_V}}=\text{áll}\mathrm{.}}\end{array}$ 2. Határozzuk meg $V$ térfogatú fotongáz hőkapacitását, azaz a $C=\Delta Q/\Delta T$ mennyiséget! Megoldás. $\begin{array}{c}{\displaystyle C=4\left(\sigma /c\right)\cdot T^3\cdot V\mathrm{.}}\end{array}$ A második főtétel, entrópia   3. Mekkora lehet egy fűtőtest optimális hatásfoka? (A közönséges hősugárzó hatásfoka $100\%$, mert a befektetett elektromos energiát teljes egészében hővé alakítja. Lehet-e ennél jobb hatásfokú készüléket csinálni?)   4. Bizonyítsuk be, hogy a sötétebb testek a sugárzó hőt nemcsak könnyebben nyelik el, hanem könnyebben ki is sugározzák!   5. Egy szilárd test fajhője általában jó közelítéssel állandó, vagyis igaz a $\begin{array}{c}{\displaystyle \Delta Q=c\cdot N\cdot \Delta T}\end{array}$ összefüggés. Általában a test tágulásakor végzett térfogati munka is elhanyagolható. E két feltevéssel határozzuk meg az entrópiát mint az energia, részecskeszám és a térfogat függvényét!   Megoldás. A második feltevésből következik, hogy $\begin{array}{c}{\displaystyle \Delta E=\Delta Q-p\cdot \Delta V=\Delta Q=c\cdot N\cdot \Delta T}\end{array}$ azaz $\begin{array}{c}{\displaystyle E=c\cdot N\cdot T\mathrm{.}}\end{array}$ Másrészt $\begin{array}{c}{\displaystyle \Delta Q=T\cdot \Delta S=c\cdot N\cdot \Delta T\to \Delta S/\Delta T=\left(1/T\right)\cdot c\cdot N\mathrm{.}}\end{array}$ Az utóbbi összefüggés akkor teljesül, ha ($T_0$ állandó) Felhasználva az előbb kapott eredményt Az entrópia ebben a közelítésben a térfogattól nem függ. 6. Az előző feladat eredményeit felhasználva mutassuk meg, hogy ha egy zárt rendszerben $0{}^{\circ }\text{C}$-os olvadó jég és egy $10{}^{\circ }\text{C}$-os rézdarab van egymástól fallal elválasztva, akkor miután a falat kivesszük és a rézdarab is $0{}^{\circ }\text{C}$-ra hűl, a rendszer entrópiája megnő!   Megoldás. A réz entrópiája csökken: $\begin{array}{c}{\displaystyle \Delta S_{\text{<span style="font-style: italic;">réz</span>}}=c\cdot N\cdot \left[\text{ln}\left(T_2/T_0\right)-\text{ln}\left(T_1/T_0\right)\right]=c\cdot N\left(\text{ln}273-\text{ln}283\right)=c\cdot N\cdot \left(-0\mathrm{,}036\right)\mathrm{.}}\end{array}$ Az olvadó jég entrópiája nő: $\begin{array}{c}{\displaystyle \Delta S_{\text{<span style="font-style: italic;">jég</span>}}=\frac{\Delta Q}{T_2}=\frac{cN\left(T_2-T_1\right)}{T_2}=c\cdot N\cdot 0\mathrm{,}037.}\end{array}$ A két változás összege pozitív $\begin{array}{c}{\displaystyle \Delta S=c\cdot N\cdot 0\mathrm{,}001>0.}\end{array}$ A feladat eredményét az entrópianövekedés tételével összevetve magyarázatot kaphatunk arra, hogy a folyamat fordítottja miért nem játszódik le magától. A harmadik főtétel 7. Bizonyítsuk be, hogy az ideális gáz állapotegyenlete $T\to 0$-nál nem írhatja le valóban létező anyag viselkedését! ${}^{*}$Az Eötvös Loránd Fizikai Társulat Ifjúsági Fizikai Körén 1974 második félévben elhangzott előadások összefoglalója.