Cím: Tél van
Szerző(k):  Csirmaz László 
Füzet: 1977/december, 217 - 218. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tél van. Hullanak a hópelyhek az ablakunk előtt. Milyen alakúak? Mi történik velük? Amikor elindul egy hópehely, szabályos csillaghatszög alakja van. Tegyük fel, hogy útja során minden másodpercben határának minden egyenes szakasza középső harmadában egy szabályos háromszög nő ki a pehelyből. Először tehát 12 kis háromszög nő a csillag száraira (1. ábra).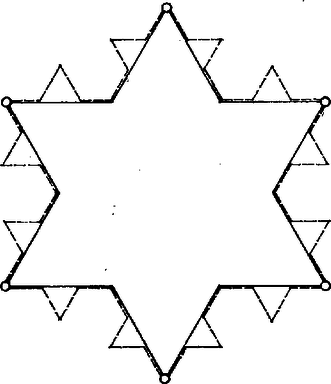

 

 

1. ábra
 

Az első másodperc végén 48 egyenlő éle van a pehelynek, a második másodpercben ezek töredeznek szét, hogy 24 újabb szabályos háromszög csatlakozhasson. És ez így megy tovább, amíg a pehely száll. Hirtelen szél kerekedik, felkapja a pelyheket, és elviszi őket messze, messze, el a végtelenbe. Hogy fognak kinézni, mire odaérnek? Milyen hó esik a végtelenben? Lesz-e a pelyheknek határvonaluk, területük, és lesz-e nekik egyáltalán kerületük?
Nézzük csak! Ha a hópelyhek síklények, és van végtelen, és egy most született pehely súlya s0=1 pond, az első másodperc végén súlya s1=1+19 pond lesz, az n-edik másodperc végén
sn=1+19+481+...+14(49)n=34+14∑i=0n(49)i=34+14⋅1-(49)n+11-49=1,2-15(49)n
pond lesz. Ahogy tehát a pehely tart a végtelenbe, súlya 1,2 pondhoz tart.
Mit csinál a kerülete? Ha kezdetben k0=1cm, az első másodperc után k1=43cm, az n-edik másodperc végén kn=(43)ncm. Baj van, ennek a határértéke +∞. Valahol tévednünk kellett! Miért hittük azt, hogy a végtelenben a hópehely kerülete egyenlő kerülete határértékével? Mi van, ha a szél elviszi a lépcsőnket, és az is csipkéket kezd növeszteni a 2. ábra szerint?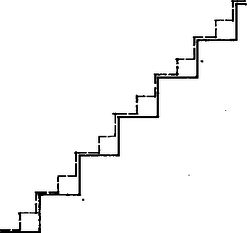
 

 

2. ábra
 

Útja során lépcsőnk hossza változatlan marad, de a végtelenben hopp, lecsökken a 2-ed részére.
Különben is, miért hittük, hogy van a hópehelynek kerülete a végtelenben? Egyáltalán honnan tudjuk, hogy van ott hópehely?
Meg kell nyugtatnunk az olvasót, legalábbis ami a kérdés második felét illeti. A végtelenbeli hópehely valóban létezik, sőt bizonyos értelemben elég közönséges: határát kölcsönösen egyértelműen és (mindkét irányban) folytonosan le lehet képezni a körvonalra, belsejét pedig a körlemezre (itt akármelyik kör megfelel). Ennek bizonyítása nem túl bonyolult, azonban a felhasznált technikai jellegű tételek elmagyarázása (és egyáltalán, felsorolása) sokáig tartana. Elégedjünk meg azzal, hogy a tétel igaz, amit úgy is szoktak mondani, hogy a határ homeomorf a körvonallal, a hópehely maga pedig a körlemezzel. Ha egy nagyon rugalmas gumilapunk van, akkor azt pontosan rá tudjuk illeszteni a hópehelyre, anélkül, hogy a gumilapot valahol elszakítani vagy összeragasztani kellene.
Térjünk vissza a hópehely kerületére. Ha egy pont csúcsa valamelyik "csipkének'', akkor csúcsa lesz az összes továbbinak is. Ez pedig éppen azt jelenti, hogy a csipkék csúcsai pontjai lesznek a végtelenbeli hópehely határának. S mivel két pont között a legrövidebb út az egyenes, ezért a hópehely kerülete biztosan nagyobb, mint ha a kerület pontjaiból bizonyosakat kiveszünk, és azokat (sorrendben) szakaszokkal összekötjük. Ezért a hópehely kerülete biztosan nagyobb, mint akármelyik csipke kerülete, azaz nagyobb vagy vagy egyenlő sup{(4/3)n}-nél. Ilyen szám azonban nincs így azt kaptuk, hogy a hópehelynek nincs kerülete. Hópelyhünknek tehát egy igen érdekes tulajdonsága van: véges területtel rendelkezik, de nincs kerülete. (Fordítva nem lehetséges: egy körrel homeomorf alakzatnak mindig van területe.)
A hópehelygörbét először F. Kasner amerikai matematikus adta meg 1901-ben. A görbét azért konstruálta, hogy folytonos, de sehol sem differenciálható függvényt tudjon segítségével megadni. Azt, hogy a hópehely határa folytonos, már tudjuk. Belátjuk még, hogy semelyik pontjában sem lehet érintőt húzni hozzá. Megszoktuk, hogy egy pontban akkor nem lehet érintőt húzni, ha ott "csúcs'' van. Ilyen értelemben a hópehelygörbének mindenhol csúcsa van.
Egy görbe P pontjában húzott érintőt definiálhatjuk úgy is, mint a PQ egyenes határhelyzetét, ha a Q pont a P ponthoz közeledik a görbén. Ezért ha a Q pont "elég közel van'' P-hez, akkor PQ-nak és az érintőnek szöge mindenképpen kisebb lesz, mondjuk 10∘-nál, és így a Q1 és Q2 pontokat választva, PQ1 és PQ2 szöge kisebb 20∘-nál. Ha most P-hez akármilyen közel tudunk találni olyan Q1 és Q2 pontokat, hogy PQ1 és PQ2 szöge legalább 30∘, akkor ezzel bizonyítottuk, hogy a P pontban nem lehet érintőt húzni. Ezt fogjuk tenni.
Legyen tehát adva egy P pont a hópehely határán és valamilyen kis távolság. Azt akarjuk, hogy PQ1 és PQ2 távolságok ennél kisebbek legyenek, de az egyenesek szöge 30∘-nál nagyobb legyen. Nézzük az egyik olyan csipkét, amelynek oldala kisebb a megadott távolságnál. Könnyen látható, hogy ha minden oldal fölé a 3. ábrán látható vonalkázott háromszögeket illesztjük, akkor az összes további csipke a vonalkázott részbe vagy annak határára esik, így az ilyen pontok limesze, a P pont i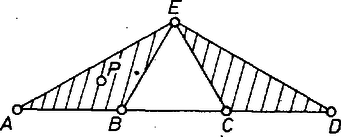s.
 

 

3. ábra
 

Másrészt az A, B, C, D és E pontok a hópehely határának pontjai, a PA, PB, PC és PE távolságok mindannyian kisebbek az AD oldalnál, így a megadott távolságnál. Végül (a P pont helyzetétől függően) vagy a PA és PB, vagy pedig a PC és PE egyenesek szöge lesz legalább 30∘-os.
Kicsit tüskések a végtelenbeli hópelyhek, de azért ez nem zavarja az ottani gyerekeket abban, hogy jó kiadós hógolyócsatát vívjanak.
(A borító 4. oldalán egy hópehely képe látható.)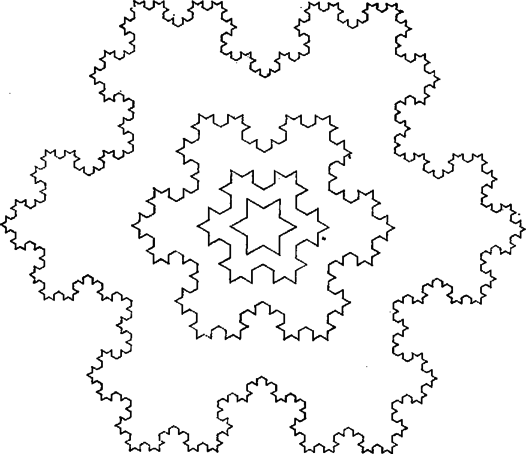