|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A múlt század vége felé a kristályok szerkezetének beható vizsgálata kiindulópontja lett a geometria egy ága, a diszkrét‐geometria kialakulásának. Az Értelmező Szótár szerint a "diszkrét'' szónak több jelentése is van, ebben az esetben kb. az értendő rajta, hogy "elkülönült tagokból álló'' ‐ matematikai szempontból ellentéte a "folytonos'' jelző. Az alábbiak bepillantást engednek a diszkrét‐geometria tárgykörébe, valamint abba, hogy miért kapta ezt a nevet.
A geometria ezen ága keletkezését Axel Thue (1863‐1922) norvég matematikus 1892-ben megjelent alapvető értekezésétől szokták számítani. Ebben a tanulmányban Thue lényegében arra a kérdésre keresett választ, hogy egymásba nem nyúló, egyenlő körlapokkal a sík hanyadrésze tölthető ki; vagy másként: a sík egybevágó körökkel való kitöltései sűrűségének mi a felső határa. Gondoljunk pl. egy nagy asztallapra. Kérdés, miként kell arra egyforintosokat helyeznünk, hogy azok az asztal lehető legnagyobb százalékát lefedjék? Említett értekezésében Thue bebizonyította, hogy egymásba nem nyúló, egyenlő sugarú körlapokkal a síknak legföljebb -ed része, tehát %-a fedhető le. Ezt az értéket el is érjük akkor, ha minden kört hat másik érint kívülről. Az eredmény nem meglepő, de bizonyítása körülményes.
A Thue-féle eredmény után a diszkrét‐geometriában mintegy 30 éve következett be nagyarányú fellendülés, mikoris a vizsgálatokat számos irányba terjesztették ki (pl. a legsűrűbb gömbelhelyezés kérdésére is). Az elért eredmények sok problémáját a gyakorlati életben adódó kérdések vetették fel. Nálunk igen gazdag hagyományai vannak e kutatási területnek, számos hazai matematikus járul hozzá a diszkrét‐geometria ma is állandóan bővülő és jelentőségében is fokozódó elméletéhez.
* A világhirű magyar matematikus, Bolyai Farkas (1775‐1856) "Tentamen'' c. kétkötetes munkájában (először 1832‐33-ban jelent meg) találunk egy olyan feladatot, mely a diszkrét‐geometriához tartozik. Az alábbiakban ezt ismertetjük, a Ti feladatotok, hogy a közölteket számítással ellenőrizzétek.
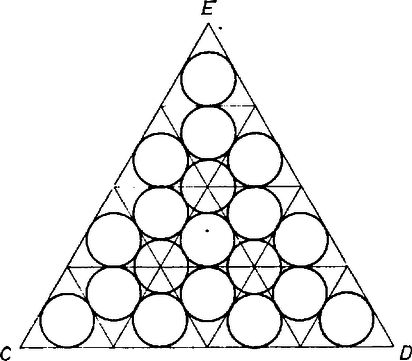
Az sugarú körbe írt szabályos háromszög területe: Osszuk fel a háromszög oldalait egyenlő részre (a Tentamenben ), és az osztópontokon áthaladó, a háromszög oldalaival párhuzamos egyenesekkel daraboljuk fel számú kisebb háromszögre. Írjunk ezekbe köröket. A beírt körök között maradnak hézagok, ezekbe ismét rajzolhatunk az előbbiekkel egybevágó, azokat kívülről érintő köröket (e körök középpontjai a háromszög oldalaival párhuzamos egyenesek metszéspontjai, l. az ábrát).
Ilyen módon a háromszögbe számú kongruens kört írunk. A körök által lefedett terület: | | (2) |
A feladatban Bolyai Farkas a következőket kérdezi:
1. Mennyi a le nem fedett része, vagyis ? A le nem fedett részt ő vakuitásznak nevezi (vákuum = űr, légüres tér).
2. Létezik-e, és ha igen, mennyi az határértéke, ha a végtelenhez tart?
Az 1. kérdésre a választ közvetlenül megadja (1) és (2) különbsége. Ebből pedig azonnal belátható, hogy a 2. kérdésre igenlő a válasz, és | | (3) |
Figyelembe véve ezek után (1)-et és (3)-at, megközelítő számítással igazolható a Tentamenben levő következő egyenlőtlenség: Egyébként (3)-ből közvetve az is kiszámítható, hogy esetén a háromszög 90,689...%-át fedik körök. Vessük össze ezt a számot a Thue által talált eredménnyel!
A Bolyai-példa nyilván a diszkrét-geometriába illik, de itt a szerkesztés módja már eleve biztosítja a háromszögnek egybevágó körökkel való maximális lefedését. Föltételezhetjük, hogy Bolyai Farkas gyakorlati probléma ‐ erdőtelepítés, kertészkedés ‐ során bukkant erre a kérdésre, hisz ilyesmikkel is foglalkozott matematikai szempontból. |
 PDF | MathML
PDF | MathML