Cím: 1976. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Pelikán József ,  Surányi János 
Füzet: 1977/február, 50 - 62. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Egy paralelogramma csúcsai a körüljárás sorrendjében: A, B, C, D. A paralelogrammán kívül levő P pontra a PAB és PCB szögek nagysága egyenlő, irányításuk pedig ellentétes.
Bizonyítsuk be, hogy ekkor APB∢=DPC∢.

 
I. megoldás. Állapítsuk meg először, hol helyezkedik el a P pont. Megmutatjuk, hogy nem lehet az AB, AD félegyenesek meghatározta, C-t tartalmazó szögtartományban. Valóban, az itt fekvő P pontokra* a PAB∢ része a DAB∢-nek, a PCB∢ viszont tartalmazza a DAB∢-gel egyenlő DCB∢-et.
 
 

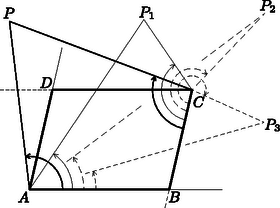1. ábra
 

Hasonlóan nem lehet P az A-t tartalmazó DCB szögtartományban sem, tehát vagy az AB és CB egyenesek B-n túli meghosszabításai közti kenvex szögtartományban van, vagy AD-nek és CD-nek a D-n túli meghosszabításai közt.
Feltehetjük, hogy az előbbiben, mert ellenkező esetben az ellentétesen irányított BAP és BCP szögekkel együtt a paralelogramma A-nál, ill. C-nél levő szögével csökkentett DAP és DCP szögek nagysága is egyenlő és irányításuk ellentétes. Így tükrözve a paralelogramma középpontjára, visszavezettük a problémát arra az esetre, amikor P az AB és CB meghosszabbítása határolta tartományban van.
Toljuk el a P pontot a BC vektorral. Új helyzete legyen P1 (2. ábra). Ekkor a DCP1 háromszög az ABP háromszög eltolt képe, BPP1C pedig paralelogramma. A P1DC∢ és a PAB∢ irányítás és nagyság szerint megegyezik. Utóbbi a feladat feltétele szerint a BCP∢-gel egyezik meg nagyságban és irányításra is, ez pedig a P1PC∢-gel, mert a BPP1C paralelogramma középpontjára való tükrözés egymásba viszi át a kettőt.
 
 

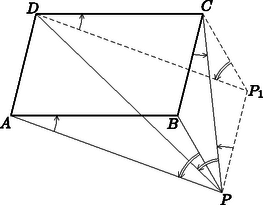2. ábra
 

Azt nyertük tehát, hogy a P-t és a D-t P1-gyel összekötő egyenest egyező irányban egyenlő szöggel elfordítva kapjuk a C-n átmenő egyeneseket. Ez azonban azt is jelenti, hogy C, D, P és P1 egy körön van. Ekkor a P-t és P1-et C-vel összekötő egyeneseket is egyező irányú és nagyságú forgás viszi át a P-t ill. P1-et, D-vel összekötő egyenesekbe. A P1C, P1D egyeneseket viszont CB vektorral eltolva a PB, PD egyeneseket kapjuk. Az előbbit az utóbbiba tehát ugyanolyan irányú és nagyságú forgás viszi át, mint PC-t PD-be. Ezzel a feladat állítását bebizonyítottuk.
 
Megjegyzések. 1. A kerületi szögek tételét nem egészen megszokott formában fogalmaztuk meg. Ezt azért tettük, mert ebben a formában szükséges és elégséges feltételét kapjuk annak, hogy négy pont egy körön feküdjék, anélkül, hogy vizsgálni kellene a pontok egymáshoz viszonyított elhelyezkedését a síkban.
Az A, B, U, V pontok akkor és csak akkor vannak egy körön, ha az AU és BU egyenest ugyanolyan nagyságú és irányú elforgatás viszi át az AV, ill. BV egyenesbe (3. ábra).
 
 

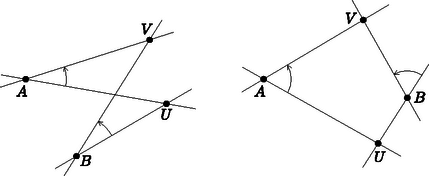3. ábra
 

A tétel ilyen megfogalmazását használva elhagyhatjuk azt a feltevést is, hogy a P pont a paralelogrammán kívül van. Minden esetben igaz, hogy ha a feladat további feltételei teljesülnek, akkor a P-t B-vel, ill. C-vel összekötő egyenes egyező nagyságú szöggel forgatható egyező irányban az A-val, ill. D-vel összekötő egyenesbe. A fenti bizonyítás változtatás nélkül érvényes marad, amint az a 4. ábrán könnyen követhető.
 
 

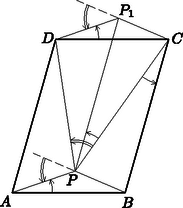4. ábra
 

2. Az előző megjegyzésben megfogalmazott tételt, illetőleg annak megfelelő összefüggéseket általában a középponti és kerületi szögek közti összefüggésből szokás levezetni, a tétel azonban könnyen belátható közvetlenül is.
 
Először kissé módosítjuk a kerületi szög és a belefoglalt körív fogalmát. Kerületi szögnek nevezzük két egyenes szögét, ha az egyenesek a kör kerületén metszik egymást. Tekintsük az egyenesek másik metszéspontját a körrel. A két egyenes szöge által befoglalt köríven a körnek a metszéspontok közti két íve közül azt értjük, amelyiket a két egyenes adott nyílásszögű szögtartománya tartalmaz. Ha az egyenesek irányított szögét tekintjük, akkor a befoglalt ívet is irányíthatjuk az első szögszárral való metszésponttól a második szögszárral való metszéspont felé. Nem zárjuk ki azt sem, hogy az egyik szögszár érintő legyen; ez esetben az ezzel a szárral való ,,második metszéspont'' is jelentse az érintés pontot (5. ábra).
 
 

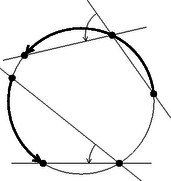5. ábra
 

A kerületi szög ilyen értelmezésével megengedtünk olyan eseteket is, amelyeknél a szög csúcsa a befoglalt köríven van és nem csak a 180∘-ra kiegészítő szöget tekintjük mint a teljes körré kiegészítő íven nyugvó kerületi szöget.*
A következő tételt bizonyítjuk be:
Adott kör két (irányított) kerületi szöge akkor és csak akkor foglal be nagyságra és irányra egyenlő íveket, ha egyenlők.
A tételből nyilvánvalóan következik az előző megjegyzésben kimondott tétel. Ha ugyanis A, B, U, V egy körön fekszik, akkor az AU, AV egyenesek szöge is, a BU, BV egyeneseké is ugyanazt az UV ívet foglalja magába, tehát egyenlők.
Ha viszont AU és AV nagyságra és irányra ugyanakkora szöget határoz meg, mint BU és BV, akkor először is nem lehet A, B és U egy egyenesen, mert akkor AU-val, ill. BU-val egyenlő szöget bezáró egyenesek párhuzamosak lennének, nem lehetne egy közös V metszéspontjuk, kivéve, ha egybeesnek ekkor sincs azonban egy meghatározott V metszéspont.
Létezik tehát egy egyértelműen meghatározott, A-n B-n, és U-n átmenő kör. Messe ez AV-t V'-ben. Ekkor BU és BV' szöge megegyezik AU és AV szögével, tehát feltétel szerint BU és BV szögével is, BV tehát egybeesik BV'-vel és így AV-vel való V metszéspontja is V'-vel. Ez azonban éppen azt jelenti, hogy A, B, U, V egy körön van, és ezt akartuk belátni.
Bizonyítsuk be ezután a fönt kimondott tételt, legyen a körben két kerületi szög. Az egyiket alkossák az e és f egyenesek, a másikat a g és h egyenesek. Forgassuk el az utóbbit úgy, hegy az elforgatott g1 és h1 egyenes közül g1 legyen párhuzamos e-vel. Jelöljük a szögek csúcsát A-val, ill. B-vel, e, f, g1, h1 másik metszéspontját a körrel E, F, G1, H1-gyel (6. ábra).
 
 

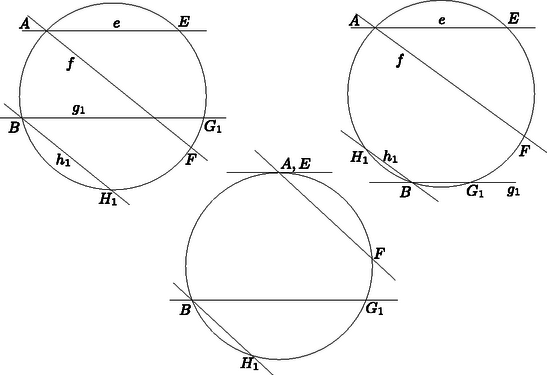6. ábra
 

 
Két állítást kell belátnunk.
a) A szögek egyenlőségéből következik az íveké: ha e és f szöge megegyezik g1 és h1 szögével, akkor h1 is párhuzamos f-fel. Az AE és BG1 párhuzamos húrok felező merőlegese a körnek egyaránt átmérője és párhuzamosak, tehát egybeesnek. Az EG1 ívnek erre az átmérőre vett tükörképe az AB ív, ezek tehát egyenlők és ellentétes irányúak. Hasonlóan az FH1 ív is egyenlő AB-vel és ellentétes irányú, tehát EG1 és FH1 egyező irányú és nagyságú. Ekkor azonban EF és G1H1 is egyező irányú és nagyságú, mert az előbbi az EG1 és G1F ívek összege, az utóbbi pedig G1F-ből az FH1 ív hozzáadásával keletkezik.
b) Az ívek egyenlőségéből következik a szögeké: Ha az EF és G1H1 ívek irányra is, nagyságra is megegyeznek, akkor EG1=EF+FG1 és FH1=FG1+G1H1 ívek is megegyeznek. Mivel e∥g1 most is fennáll, így EG1 és AB egyező nagyságú és ellentétes irányú ívek. Ekkor azonban ugyanez áll az AB és FH1 ívekre is. Ha tehát tükrözünk az AF húrt merőlegesen felező átmérőre, akkor B tükörképe H1 lesz. Eszerint a BH1 egyenes, vagyis h1 is merőleges a tükörtengelyre, tehát párhuzamos f-fel. Ekkor azonban g1 és h1 szöge megegyezik e és f szögével, és ezt kellett belátnunk.
 
II. megoldás. A P pont rombusz esetén a BD átló egyenesének a paralelogrammán kívüli részén van, mert a BD-re való tükrözés A-t C-be és így a BAP szöget a BCP szögbe viszi át.
Ha a paralelogramma nem rombusz, akkor mérjük az A-ból induló és B-n átmenő félegyenesre az AB1=AD távolságot. A B1-en át AD-vel párhuzamosan húzott egyenes messe a CD egyenest C1-ben. Egy P1 pont, amely az AB1C1D paralelogrammára vonatkozóan elégíti ki a feladat feltételeit, a DB1 átló egyenesén van. Szimmetria folytán feltehetjük, hogy a B1-en túli meghosszabbításon (7. ábra).
 
 

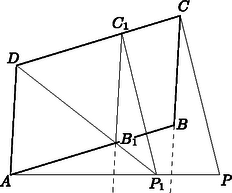7. ábra
 

Toljuk el a B1C1P1, szöget úgy, hogy B1C1 menjen át BC-be. Ekkor P1 az AP1 egyenes mentén mozdul el és jut a P pontba. Ez a BC egyenes ellenkező partján van mint A, másrészt az egész A-ból induló P1-en átmenő félegyenes AB ellenkező partján van, mint a paralelogramma. Így P az AB és CB egyenesek B-n túli meghosszabbításai határolta síkrészben van.
Messe AB és CB egyenese a CP, ill. AP egyenest E-ben, ill. F-ben. Megmutatjuk, hogy az APCD és EPFB négyszögek hasonlóak, a csúcsokat felsorolt sorrend szerint feleltetve meg egymásnak. (8. ábra)
 
 

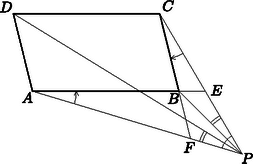8. ábra
 

Valóban P-nél levő szögük közös; másrészt EBF∢=ABC∢, mert egymás csúcsszögei, viszont ABC∢=ADC∢; végül BEP∢=DCP∢=DAP∢. Az utóbbi egyenlőség épp a feladat feltétele folytán áll fenn.
Az ABF és CBE háromszög hasonló, mert A-nál és C-nél feltétel szerint egyenlő szög van, a B-nél levő szögek pedig csúcsszögek. Ebből következik, hogy
BEBF=BCBA=ADCD,
azaz a két négyszög egy-egy egymásnak megfelelő oldalpárjának az aránya is megegyezik. Ebből már következik a két négyszög hasonlósága és ebből az, hogy az átlók az egymásnak megfelelő oldalakkal egyenlő szöget zárnak be. Így APD∢=EPB∢=CPB∢. Ezzel a feladat állítását bebizonyítottuk.
 
Második feladat. Valaki 55(=3125) szelvénnyel lottózik. Bármely két szelvényét nézzük, van olyan szám, amely mindkét szelvényen meg van ikszelve.
Bizonyítsuk be, hogy az 1-től 90-ig terjedő számok között található 4 olyan, hogy az illető mindegyik szelvényén a 4 szám közül legalább az egyik meg van ikszelve.
 
Megoldás. Feltesszük, hogy a különféle lottószelvények különféleképpen vannak kitöltve. Vegyünk egy tetszőleges L1 lottószelvényt. A többi 55-1 db lottószelvény mindegyike tartalmazza az L1-en levő 5 szám valamelyikét. Az L1-en levő 5 szám közül tehát legalább az egyiket a többi szelvények közül legalább 54 tartalmazza. Válasszunk ki egy ilyen számot, jelöljük ezt a-val. a-t tehát (L1-et is beleszámítva) több, mint 54 szelvény tartalmazza. Ha minden szelvény tartalmazza a-t, akkor az állítás helyes. Ha nem, legyen L2 egy olyan szelvény, amely nem tartalmazza a-t. Az a-t tartalmazó, több mint 54 szelvény mindegyike tartalmaz legalább egy L2-n levő számot. Tehát az L2-n levő 5 szám közül legalább az egyiket (mondjuk b-t) az a-t tartalmazó szelvények közül több, mint 53 kell, hogy tartalmazza. Ha minden szelvény tartalmazza a és b közül legalább az egyiket, készen vagyunk. Ha nem, legyen L3 egy sem a-t, sem b-t nem tartalmazó szelvény. A fenti gondolatmenetet megismételve találunk L3-on egy olyan c számot, hogy több mint 52 szelvény van, amelyik a, b, c mindegyikét tartalmazza. Ismét készen vagyunk, vagy van olyan L4 szelvény, ami a, b, c egyikét sem tartalmazza, és ekkor ezen találunk olyan d számot, hogy több, mint 5 szelvény tartalmazza a, b, c, d mindegyikét. Ha lenne olyan L5 szelvény, amelyik a, b, c, d egyikét sem tartalmazná, akkor az L5-ön levő öt szám egyike, mondjuk e, olyan lenne, hogy több, mint 1 szelvény lenne, amelyik a, b, c, d, e mindegyikét tartalmazná. Mivel ez feltevésünk szerint lehetetlen, bebizonyítottuk, hogy az a, b, c, d számnégyes rendelkezik a kívánt tulajdonsággal.
Megjegyzések. 1. Arra a feltevésre, hogy különböző szelvények különbözőképpen vannak kitöltve, valóban szükség van. Könnyen konstruálhatunk olyan példát, ami ezt mutatja. Válasszunk ki pl. az első 9 természetes szám közül minden lehetséges módon 5-öt. Ez (95)=126-féleképpen lehetséges.Ezután az 55 szelvény mindegyikén ezen ötösök valamelyikét jelöljük ki, mégpedig a 126 db ötös mindegyike legalább egy szelvényen legyen kijelölve. Könnyen látható, hogy ekkor bármely két szelvény tartalmaz közös számot, mégsem találhatunk a mondott tulajdonsággal rendelkező számnégyest.
2. Ha veszünk 55 db különbözőképpen kitöltött lottószelvényt, úgy hogy bármely kettőnek van közös eleme, akkor világos, hogy van 5 olyan szám, hogy minden lottószelvény tartalmazza ezen 5 szám közül legalább az egyiket. Pl. akármelyik lottószelvényen megjelölt 5 szám megfelel. Nehezebb (és éppen ez volt a feladat állítása), azt bizonyítani, hogy már 4 szám is található a kívánt módon.
Nem javítható-e a 4 tovább 3-ra, azaz nem igaz-e, hogy mindig van 3 olyan szám, hogy mindegyik lottószelvény tartalmazza e 3 szám valamelyikét? Megmutatjuk, hogy nem.
Rendezzük el az 1-től 10-ig terjedő számokat az alábbi séma szerint:
 
12345678910

 
Válasszuk ki ezek után az összes olyan számnégyest, amit úgy kapunk hogy valamelyik szintről az összes számot vesszük, minden alatta levő szintről 1‐1 számot veszünk, a fölötte levő szintekről pedig nem veszünk számokat.
Ilyen négyesek pl.:
  1258  1267  23410  4568  78910

Összesen
4!1!+4!2!+4!3!+4!4!=4⋅3⋅2+4⋅3+4+1=41
ilyen számnégyes van. Könnyen látszik, hogy bármely kettőnek van közös eleme, és nem található 3 olyan szám, hogy mind a 41 számnégyes tartalmazná ezen 3 szám valamelyikét.
Vegyük ezután hozzá mindegyik négyeshez a 11-től 90-ig terjedő számok mindegyikét. Így
41⋅80=3280
számötöst kapunk úgy, hogy bármely kettőnek van közös eleme és nincs 3 olyan szám, hogy mindegyik számötös tartalmazná e 3 szám valamelyikét. E számötösök száma még több is, mint a kívánt 3125=55. Ha azt akarjuk, hogy számuk pontosan 3125 legyen, hagyjunk el 155 db-ot közülük, csak arra vigyázva, hogy az elhagyás után is még mind a 41 számnégyest legalább egy megmaradt számötös tartalmazza. Nem nehéz belátni, hogy ez a konstrukció rendelkezik a kívánt tulajdonsággal.
3. Mint látható, a feladat bizonyításában nem használtuk ki, hogy éppen 90 szám közül választhatók az ötösök. Valójában azt bizonyítottuk, hogy akárhogy választunk (bármely elemekből képzett) 55 db 5-elemű halmazt úgy, hogy bármely két halmaznak van közös eleme, akkor mindig található 4 olyan elem, hogy mind az 55 db halmaz mindegyike tartalmazza e 4 elem közül legalább az egyiket.
Általánosabban a következő igaz: ha van nn db n elemű halmaz (n≥2) úgy, hogy bármely kettőnek van közös eleme, akkor található (n-1) db elem úgy, hogy bármely halmaz tartalmazza ezen (n-1) elem közül legalább az egyiket. Ennek bizonyítása teljesen megegyezik a fent közölt bizonyítással, csak éppen az ott szereplő gondolatmenetet nem 5, hanem n lépésen keresztül kell megismételni.
4. Az eddig tárgyalt problémakör matematikai tartalma még általánosabban a következő: Ha vannak n elemű halmazok úgy, hogy bármely kettőnek van közös eleme, továbbá tudjuk, hogy nem található n-nél kevesebb elem úgy, hogy mindegyik halmaz tartalmazza ezen elemek valamelyikét, akkor ezek az n elemű halmazok nem lehetnek sem túl sokan, sem túl kevesen.
Mennyi itt a ,,túl sok''? A 3. megjegyzésben láttuk, hogy nn-t már biztosan nem érheti el a számuk. Másrészt a 2. megjegyzésben leírt konstrukciót n szintből álló számháromszögre általánosítva látjuk, hogy
n!1!+n!2!+...+n!n!=[(e-1)⋅n!]
n elemű halmaz még található a fent leírt módon.
(Itt e=2,71828... és [x] jelöli a legnagyobb olyan egész számot, amelyik nem nagyobb x-nél.)
Nagy n-re [(e-1)⋅n!] sokkal kisebb, mint nn. Hogy [(e-1)⋅n!] és nn között hol kezdődik a ,,túl sok'', nem tudjuk.
Mennyi a ,,túl kevés''? Nem nehéz belátni, hogy 2(n-1) már túl kevés. Ha ugyanis legfeljebb ennyi halmazunk van, akkor kettenként választhatunk hozzájuk egy-egy elemet, ami annak a kettőnek mindegyikében benne van, (hiszen bármely két halmaznak van közös eleme) és így legfeljebb (n-1) elemre lesz szükségünk.
Véges projektív síkok* segítségével tudunk olyan halmazszámot is megadni, amennyi már nem ,,túl kevés''. Vegyünk egy olyan véges projektív síkot, amelyen minden egyenesnek n pontja van. Ilyen mindig található, ha n-1 prímhatvány. Az egyenesek lesznek a szóban forgó n-elemű halmazok, számuk n2-n+1. Bármely kettő metszi egymást, és nem nehéz belátni, hogy nem adható meg úgy (n-1) pont, hogy minden egyenes tartalmazza legalább az egyiket közülük. Finomabb módszerek alkalmazásával Erdős Pál és Lovász László kimutatta, hogy a ,,túl kevés'' valahol 83n-3 és c⋅n3/2⋅logn között ér véget, ahol c alkalmas konstans. Hogy pontosabban hol van ez a határ, az ez idő szerint szintén nem ismeretes.
 
Harmadik feladat. Tegyük fel, hogy egy másodfokú (valós együtthatós) polinom minden (valós helyen felvett) helyettesítési értéke pozitív. Bizonyítsuk be, hogy ekkor a polinom előállítható két pozitív együtthatós polinom hányadosaként.
 
I. megoldás. Legyen a kérdéses polinom
f(x)=ax2+bx+c.
A feladat másodfokú polinomról szól, tehát a≠0. Ha a polinom csak pozitív értékeket vesz fel, akkor
f(0)=c>0.

Megmutatjuk, hogy a is pozitív. Írjuk f-et
a(x+b2a)2+c-b24a2(1)
alakban. Itt az utolsó két tag állandó. Az első tag második tényezője tetszés szerint naggyá tehető x alkalmas megválasztásával. Így ha a negatív volna, akkor a polinom venne fel negatív értéket is.
Feltehetjük, hogy a=1, mert f és 1af mindegyike a másikból egy pozitív számmal való szorzással kapható. Ez a művelet pozitív együtthatós polinomok hányadosát újra ilyenbe viszi át, ha pl. a hányados számlálóját szorozzuk a számmal.
Ha b pozitív, akkor az 1 konstans polinom nevezővel kapunk egy kívánt alakú előállítást. Ellenkező esetben célszerű az (1) előállításban szereplő b2-t jelölni (-d)-vel és a konstanst is egy betűvel, mondjuk h-val. Ekkor (1) így alakul:
f(x)=(x-d)2+h.(1')
Itt d≥0 és f(d)=h>0.
A feladat állításának igazolásához elég egy olyan pozitív együtthatós polinomot találni, amelyikkel f-et megszorozva a szorzat is pozitív együtthatós lesz.
Ha d=0, akkor pl. x+1 nyilvánvalóan megfelel a követelményeknek.
Ha d>0, akkor próbálkozzunk az
(xn+dxn-1+...+dn-1x+dn)2(2)
polinommal. Ha (1') első tagját szorozzuk, akkor
(xn+1-dn+1)2=x2n+2-2dn+1xn+1+d2n+2
adódik. Ehhez kell még (2)-nek a h-szorosát adnunk. Ebben a polinomban x minden hatványa fellép a 0-adfokútól a 2n-edfokúig pozitív együtthatóval.
Azt kell megnéznünk, tudjuk-e n-et úgy választani, hogy a kapott polinomban az (n+1)-edfokú tag együtthatója nagyobb legyen, mint 2dn+1.
Ha (2)-t két egyenlő tényező szorzataként képzeljük el, akkor az első k-adfokú tagját a második (n+1-k)-adfokú tagjával szorozva kapunk (n+1)-edfokú tagot. Ez lehetséges, ha k=1,2,...,n. Mindegyik esetben dn-1xn+1 lesz a szorzat, így (1') és (2) szorzatában xn+1 együtthatója
nhdn-1-2dn+1=dn-1(nh-2d2).
Ez az együttható pozitív, ha
n>2d2h.
Ha így választjuk meg n-et, akkor tehát a szorzat pozitív együtthatós lesz, csak a (2n+1)-edfokú tag hiányzik belőle ‐ 0 lesz az együtthatója. Ha még megszorozzuk a szorzatot pl. (x+1)-gyel, akkor már olyan polinomot kapunk, amelyikben a 0-adfokú tagtól a (2n+3)-adfokú tagig mindegyik szerepel pozitív együtthatóval. Ezzel a feladat állítását bebizonyítottuk.
 
Megjegyzések. 1. Ha másodfokú polinomon legfeljebb másodfokút értünk, akkor sem lehet, hogy másodfokú tag nem lép fel ténylegesen, de elsőfokú igen, mert minden ilyen polinom vesz fel pozitív és negatív értéket is. Egy c pozitív konstans polinom viszont írható c1 alakban mint két pozitív együtthatós polinom hányadosa.
2. Volt, aki megelégedett azzal, hogy a ténylegesen fellépő tagok együtthatója pozitív legyen, de megengedte, hogy egyes hatványok kimaradjanak, mint (1') és (2) szorzatából a (2n+1)-edfokú tag. Ha ilyen alakig sikerült eljutni, akkor már nem nehéz a feladat szigorúbb követelményeit is kielégítő polinomhoz jutni. Könnyen látható, hogy ha egy nem-negatív együtthatós polinomot, amelyben két-két előforduló tag közt legfeljebb k darab hatvány hiányzik, megszorzunk pl. az
1+x+x2+...+xk
polinommal, akkor már nem lesz kimaradó hatvány a legmagasabb fokú tagig.
3. Nem csak x2 együtthatóját választhatjuk 1-nek, x együtthatójának abszolút értékét is megváltoztathatjuk. Ha ugyanis x helyébe ry-t írunk egy pozitív r számmal, akkor
f(ry)=r2(y2-bry+cr2).
Ha itt a második tényező előállítható pozitív együtthatós P1 és P2 polinomokkal P1(y)/P2(y) alakban, akkor
f(x)=r2P1(xr)P2(xr)
f-nek egy előállítása pozitív együtthatós polinomok hányadosaként. Így írhatjuk f-et pl. x2-x+u vagy x2-2x+v=(x-1)2+w, (w=v-1) alakban.
4. Láttuk, hogy a másodfokú polinom együtthatóitól függött, hogy hányadfokú számlálóval és nevezővel sikerül azt pozitív együtthatós polinomok hányadosaként írni. A fenti eljárásban a szorzó polinom N fokszáma (az előállítás nevezőjéé)
N=2n+1>4d2h+1.

Az x2-2x+1,1=(x-1)2+0,1 polinom esetén pl. ez legalább 42-edfokú szorzót jelent. Az
(x2-2x+1,1)(x9+2,01x8+2,93x7+3,65x6+4,08x5+4,15x4+3,813x3+3,062x2++1,93x+0,492)=x11+0,01x10+0,01x9+0,001x8+0,003x7+0,005x6++0,001x5+0,001x4+0,0003x3+0,0002x2+1,139x+0,5412,(x2-2x+1,1)(1+1,82x+2,41x2+2,73x3+2,78x4+2,573x5+2,151x6+1,572x7++0,903x8+2,13x9=1,1+0,002x+0,011x2+0,003x3+0,008x4+0,0003x5++0,0001x6+0,0002x7+0,0003x8+0,0003x9+0,477x10+0,213x11,


azonosságok azt mutatják, hogy már 9-edfokú polinomok is megfelelnek (két egészen különböző felépítésű is). Az sincs kizárva, hogy még alacsonyabb fokúval is célt lehetne érni.
 
II. megoldás. A harmadik megjegyzés szerint írhatjuk a másodfokú polinomot x2-2x+v alakban. Ez csak pozitív értékeket vesz fel, ha v>1.
A második megjegyzés értelmében elég olyan nem-negatív együtthatós polinomot keresni, amivel ezt a polinomot megszorozva a szorzat is nem-negatív együtthatós lesz. Ezt a polinomot
a0+a1x+...+anxn
alakban keresve feltehetjük, hogy a0=1. Az ai-knek olyan nem-negatív számoknak kell lenniük, amelyekre
a1v-2a0≥0,aiv-2ai-1+ai-2≥0,hai=2,...,n,és-2an+an-1≥0.
Keressünk olyan ai-ket, amelyekre az első n feltételben egyenlőség áll fenn és próbáljuk n-et úgy választani, hogy az utolsó feltétel is teljesüljön. Legyen tehát
a1=2a0v=2v,ai=2ai-1-ai-2vi=2,...,n.(3)
Kérdés, megválasztható-e n úgy, hogy az utolsó egyenlőtlenség is teljesüljön. Ez az egyenlőtlenség azt jelenti, hogy ha a fenti szabályosság szerint még az (n+1)-edik elemet is képezzük a sorozatban, az már nem lesz pozitív.
A bi=aiai-1 hányadosokra (3) a következő összefüggéseket adja:
b1=a1a0=a1=2v,bi=2-1bi-1vi=2,...,n.
Olyan n-re van szükségünk, amelyre
1bn≥2,azazbn≤12.
Ismeretes és könnyen belátható, hogy minden pozitív u-ra
u+1u≥2azaz2-1u≤u.
Ezt felhasználva
bi=2-1bi-1v≤bi-1v.
Ezt az egyenlőséget (i-1)-szer alkalmazva azt nyerjük, hogy
bi≤b1vi-1=2vi.

Mivel v>1, így van egyenlőtlenségünk szerint olyan n, amelyikre bn≤12, és már láttuk, hogy elég a legkisebb ilyen n értéket megkeresnünk. Ezzel a feladat állítását bebizonyítottuk.
 
Megjegyzés. Lényegében a fenti gondolatmenet szerint készült az I. megoldás utáni 4. megjegyzés első példája, azzal a módosítással, hogy a szorzat együtthatóit nem tettük 0-vá, csak v-hez képest nagyon kicsivé, hogy utólag ne kelljen még egy magas fokú polinommal szorozni ahhoz, hogy szigorúan a feladat feltételeinek megfelelő polinomokhoz jussunk.
Eljárhatnánk úgy is, hogy an-t választjuk 1-nek, és ezután a végétől visszafelé haladva határozzuk meg az együtthatókat pl. úgy, hogy mindenütt egyenlőség teljesüljön. Eközben n értékét határozatlanul hagyjuk, addig haladunk, amíg az utolsó két nyert értékre már az első egyenlőtlenség is teljesül. Ezen az alapon készült az említett megjegyzés második példája.
 
III. megoldás (vázlat). Ismét azt mutatjuk meg, hogy találhatunk másodfokú polinomunkhoz olyan nem-negatív együtthatós polinom szorzót, amivel szorozva a szorzat is nem-negatív együtthatós lesz.
A másodfokú polinomot írhatjuk
x2-bx+c(4)
alakban, ahol b és c pozitív. Akkor lesz a polinom minden értéke pozitív, ha
b2<4c.(5)
Szorozzuk meg (4)-et az x2+bx+c polinommal. A szorzat
x4-(b2-2c)x2+c2.
Ha b2≤2c, akkor ezzel célt is értünk. Ha 2c<b2(<4c), akkor szorozzunk még x4+(b2-2c)x2+c2-tel; a szorzat
x8-((b2-2c)2-2c2)x4+c4.
Itt x4 szorzója
(b2-(2+2)c)(b2-(2-2)c),
tehát elértük célunkat, ha b2≤(2+2)c, mert a második tényező feltételei szerint pozitív. Ha nem, akkor folytatni kell az eljárást. Kérdés, hogy eljutunk-e így véges számú lépésben nem-negatív együtthatós szorzathoz.
Az n-edik lépés után ilyen alakú szorzatot kapunk:
x2n+1-bnx2n+c2n.
A bn-ek sorozata a
bn+1=bn2-2c2n(6)
képzési szabály szerint keletkezik a b0=b kezdő értékből kiindulva.
Azt szeretnénk belátni, hogy tetszés szerinti (5)-öt kielégítő pozitív b, c értékekből kiindulva bn elég nagy n-re negatív lesz. Ehhez bn-et szorzat alakban írjuk. Ezt b4 esetében így tehetjük:
b4=(((b2-2c)2-2c2)2-2c4)2-2c8=(((b2-2c)2-2c2)2-2c4-2c4)(b3+2c4)==((b2-2c)2-2c2-2+2c2)(b2+2+2c2)(b3+2c4)=(b2-(2+2+2+2)c)(b1-2+2+2c)(b2+2+2c2)(b3+2c4).



Itt egy újabb sorozat lépett fel. Ennek a képzési szabályát kicsit általánosabban, mint ahogy számításainkban szerepel, így adhatjuk meg: legyen tetszés szerinti pozitív z kiindulási értékkel
a1(z)=zésan+1(z)=2+an(z),han=1,2,...
Ekkor a fenti szorzatban az
an=an(2)
sorozat néhány tagja szerepel.
Könnyű látni, hogy adott z értékre az an(z) értékek n növekedtével növekednek, és hogy adott n-re z növekedtével an(z) is növekszik. Teljes indukcióval belátható, hogy minden n-re an(4)=4, így
an=an(2)<an(4)=4,
minden n-re.
A b4-re talált fenti előállításhoz hasonlóan minden bn szorzattá alakítható. Az első tényező b2-anc lesz, és ezt kell szorozni bk+an-kc2k-1 alakú tényezőkkel a k=1,2,...,n-1 értékekre. Ezt röviden így jelöljük:
bn=(b2-anc)∏k=1n-1(bk+an-kc2k-1)
Ezt ismét teljes indukcióval lehet belátni.
Az (5) feltétel szerint b2/c egy 4-nél kisebb érték. Azt kell belátnunk, hogy an vesz fel alkalmas n-re ennél nagyobb értéket. Ha ez igaz, akkor a legkisebb ilyen n-et n0-val jelölve az n0-nál kisebb indexű b-k pozitívok, viszont bn0 negatív, s így n0-szor ismételve szorzási eljárásunkat, nem-negatív együtthatós polinomhoz jutunk.
Tudjuk, hogy an is kisebb 4-nél minden n-re. Megmutatjuk azonban, hegy elég nagy n-re tetszés szerint közel jut 4-hez. Valóban, ha n>1, akkor
0<4-an=2-an-1=4-an-12+an-1=4-an-1an<4-an-12.
Alkalmazva ezt az egyenlőtlenséget újra és újra, egyre csökkenő indexekkel végül azt kapjuk, hogy
4-an<4-a12n-1=12n-2,
ez pedig tetszés szerint kicsi, ha n elég nagy. Ezzel a feladat állítását bebizonyítottuk.
 
Megjegyzés. Ha itt az n-edik lépés után állunk meg, akkor a szorzatban a hiányzó egymás utáni hatványok száma 2n-1 lesz, így a szorzó polinom fokszáma, ha pontosan a feladatban kitűzött célt akarjuk elérni,
2+22+...+2n+2n-1=3(2n-1)
lesz. A megoldás gondolatmenete szerint biztosan célt érünk, ha n-et úgy választjuk, hogy
12n-2<4-b2c
teljesüljön. Ez az I. megoldás utolsó megjegyzésének példája esetében 33-adfokú szorzó polinomot jelent az I. meggondolás gondolatmenetéből adódó 42-edfokúval (másfelől a megjegyzésben adott 9-edfokúval) szemben.
A feltételeket az I. megoldásban szereplő d és h együtthatókra átírva általában is az ottani korlát 3/4-e adódik ezen az úton. Ennél azonban lényegesen jobb becslés is kiolvasható n-re a követett gondolatmenetből.
Ismételten alkalmazva a talált összefüggést, azt nyerjük, hogy
4-an=4-an-1an=4-a1anan-1...a2=2anan-1...a2.
Ha itt a nevező tényezőit nem 2-vel, hanem a legkisebbikkel, a2=2+2>3,41-dal behelyettesítjük, máris a
23,41n-1<4-b2c,3,41n-1>2c4c-b2
egyenlőtlenséget kapjuk n meghatározására.
Az említett másodfokú polinom esetében legegyszerűbb ténylegesen elvégezni a beszorzásokat, és azt találjuk, hogy ezen az úton 21-edfokú polinommal érünk célhoz.
*Az ábrán a szögek iránya ellentétes

*Ezért látszott célszerűbbnek befoglalt ívről beszélni, mint arról az ívről, amin a szög nyugszik.

*A véges projektív sík definíciója és elemi tulajdonságai megtalálhatók pl. a K.M.L. 51/2 (1975. október) számában az 53. oldalon kezdődő cikkben, vagy az alábbi szakköri füzetben:
Lovász‐Pelikán‐Vesztergombi: Kombinatorika. 2. kiadás (Tankönyvkiadó, Budapest, 1972. 128. old.)