Cím: Barangolás a fák közt
Szerző(k):  Horváth Csilla ,  Székely Zsuzsa 
Füzet: 1977/május, 198 - 204. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Speciális matematikai osztályba járunk, így a gráfelmélet része tananyagunknak. Amit tanultunk, azt mondjuk most itt el, reméljük, hogy cikkünk a normál tagozatba járók számára is érthető lesz. Javasoljuk az olvasónak, hogy vegyen elő papírt, ceruzát, és egy-egy feladat megoldása előtt nézze meg, mire jut egyedül. Kérdéseket is teszünk fel, ezekre a helyes válaszokat a cikk végén adjuk meg.

 

Mi a gráf?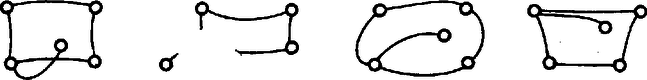
 
Pontok (szögpontok) és azokat összekötő vonalak (élek) rendszere. A pontok elhelyezkedése lényegtelen, ahogyan az élek formája is az. Csak az számít, hogy mely pontpárok vannak összekötve. Például az alábbiak közül három ugyanazt a gráfot ábrázolja. Látható, hogy az élek metszéspontját nem tekintjük szögpontnak.
 

 

Összefüggő egy gráf, ha élei mentén haladva tetszőleges pontjából eljuthatunk bármely más pontjába. Egy pont fokszámának nevezzük a belőle kiinduló élek számát. Pályának az egymáshoz csatlakozó élek összességét akkor hívjuk, ha benne minden pont foka legfeljebb kettő. Az olyan pályát, amelyen a kiindulási pontból az élek mentén haladva visszajuthatunk az eredeti pontba ‐ anélkül, hogy egy élen többször és végigmennénk ‐, körnek nevezzük. A kört tartalmazó gráfnak tehát vannak olyan pontjai, amelyeket többféle pálya is összeköt.
1. kérdés. Melyek tartalmaznak kört az alábbi gráfok közül?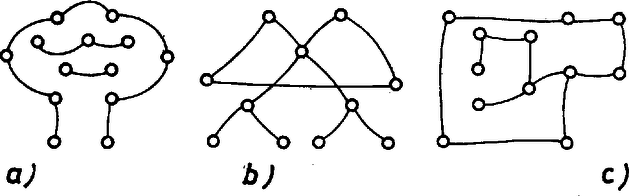
 

 

Most egy fontos gráfelméleti definíció következik. Fának nevezzük az olyan összefüggő gráfokat, amelyek nem tartalmaznak kört.
2. kérdés. A rajzok közül kettő ugyanazt a fát ábrázolja. Melyek ezek?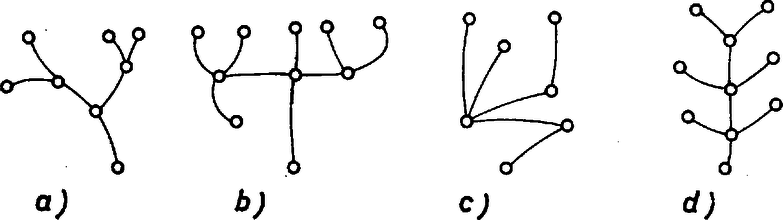
 

 

A ,,fa'' elnevezést Cayley vezette be 1857-ben. Az első, fákra vonatkozó jelentős eredményeket is ő érte el. A fa fogalma azonban régebbi. Kirchhoff például már Cayley előtt tíz évvel vizsgált fákat elektromos hálózatok tanulmányozásával kapcsolatban. Útnak nevezzük az olyan fát, amelynek nincs kettőnél magasabb fokszámú pontja.
3. kérdés. Melyik út az alábbi gráfok közül?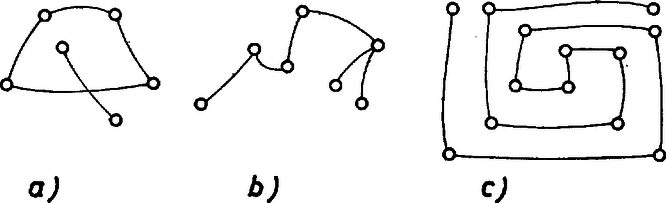
 

 

1. feladat. Hány éle van maximálisan egy n szögpontú gráfnak?
Megoldás. Ha a pontok között minden élet behúzunk, minden pontból n-1 másik pontba fut él. Összesen n pont van, így tehát n(n-1) lenne az élek száma. De gondoljuk csak meg, igy minden élet kétszer számoltunk: egyszer, amikor ,,indul'' egy pontba, és egyszer, amikor ,,befut'' egy másikba. Az élek maximális száma tehát 12n(n-1)=(n2).
 

A minimális élszám
 

2. feladat. Hány éle van minimálisan egy n szögpontú összefüggő gráfnak?
Megoldás. A minimális élszámú összefüggő gráf nem tartalmazhat kört, mivel a kör tetszőleges élének elhagyásával a gráf nem vesztené el összefüggőségét, viszont az élek száma csökkenne. Eszerint a minimális élszámú összefüggő gráf fa. Megmutatjuk, hogy minden n szögpontú fának ugyanannyi éle van. Az élek közös száma lesz a keresett minimum.
Abban a fában, amelynek egy pontjából indul ki minden éle, n-1 él van. Belátjuk, hogy minden fa átalakítható ilyen típusúvá az élek átrendezésével anélkül, hogy az élek számát csökkentenénk. Előbb azonban bebizonyítjuk, hogy minden fában van első fokú pont. Tegyük fel, hogy van olyan fa, amelyben minden pont foka nagyobb 1-nél. Induljunk el tetszőleges pályán ezen a fán egy tetszőleges pontból. Mivel minden pont foka nagyobb 1-nél, minden pontból, ahová utunk során befutunk, tovább tudunk menni. Két eset van: egyszer olyan pontba jutunk, amelyben már jártunk, vagy a pályának sosincs vége. Az első eset azért lehetetlen, mert a gráfunk fa, a második azért, mert a gráf véges. Állításunkat ezzel beláttuk.
Vegyünk egy tetszőleges fát. Tudjuk már, hogy van benne első fokú pont. Válasszunk egy tetszőleges pontot, és ha egy első fokú pont nem a kiválasztottal van összekötve, helyettesítsük a hozzá tartozó élt a kiválasztott pontból az első fokúba futó éllel. Tegyük ezt mindaddig, amíg találunk olyan első fokú pontot, amelybe nem a kiválasztott pontból fut be él. Közben se a gráf fa-volta, se éleinek száma nem változik, és végül minden él a kiválasztott pontból indul ki. Megkaptuk azt a fát, amit akartunk, készen is vagyunk. Az n szögpontú összefüggő gráfok között tehát a fáknak van a legkevesebb élük, ezek mindegyikének n-1 éle van.
Komponensnek nevezzük a gráfot alkotó, önmagukban összefüggő részeket.
4. kérdés. Legalább hány éle van az n pontú, k komponensű gráfnak?
5. kérdés. Legalább hány kör van az n pontú, k komponensű, e élű gráfban?
 
A maximális élszám
 
3. feladat. Mennyi az élek maximális száma egy n pontú nem összefüggő gráfban?
Megoldás. A maximális élszámú, nem összefüggő gráf komponenseinek a száma csak kettő lehet, különben két komponenst még összeköthetnénk egy újabb éllel anélkül, hogy a gráf összefüggővé válna. Jelöljük az egyik komponens pontjainak számát x-szel, a másikét y-nal. Ha mind a két komponensben berajzoljuk az összes élt, a kapott élek száma
e=(x2)+(y2).(1)
Elegendő tehát a következő kérdésre válaszolnunk:
6. kérdés. Mennyi (1.) maximuma, ha x+y=n, és x, y>0?
Az előző feladatra egy második megoldás adható a kiegészítő gráf fogalmának a felhasználásával. Egy G gráf kiegészítő gráfja az a G' gráf, amelynek a szögpontjai ugyanazok, mint G-nek, és amelyben két pont akkor és csakis akkor van összekötve, ha azok G-ben nincsenek összekötve.
4. feladat. Bizonyítandó, hogy ha egy gráf nem összefüggő, akkor kiegészítő gráfja összefüggő.
Megoldás. Jelöljük az eredeti gráfot G-vel, kiegészítő gráfját G'-vel. G' definíciójából következik, hogy benne G különböző komponenseinek a pontjai össze vannak kötve éllel. Legyen P és Q a G egyik komponensének két pontja, és legyen R a G egy másik komponensének a pontja. Mivel G'-ben P is és Q is össze van kötve R-rel, P és Q között is fut pálya, G' valóban összefüggő.
Könnyen látható, hogy a 4. feladat alapján új megoldást adhatunk a 3. feladatra.
 

Számozott fák
 
5. feladat. Adott n egymástól számokkal megkülönböztetett pont. Hányféleképpen lehet olyan fát előállítani, amelynek ezek a szögpontjai?
Megoldás. Nézzük meg először 4 pontra:
a) 4 olyan gráf van, ahol az egyik pontból 3 él indul ki: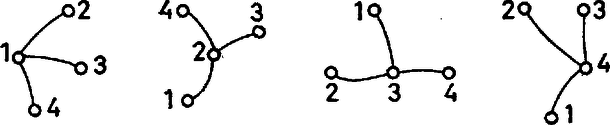
 

 

b) az olyan fák száma, melyekben 2 első fokú és 2 másodfokú pont van, (42)⋅2=12, mert a 2 első fokú pontot (42)-féleképpen választhatjuk ki a 4 közül, a két másodfokú pont pedig minden esetben felcserélhető. Ezek közül néhány:
 

 

Összesen tehát 16 különböző 4 szögpontú számozott fa van.
Számoljuk ki 5 pontra is, hátha felfedezünk valami szabályosságot!
a) 5 olyan gráf van, amikor az egyik pontból 4 él indul ki: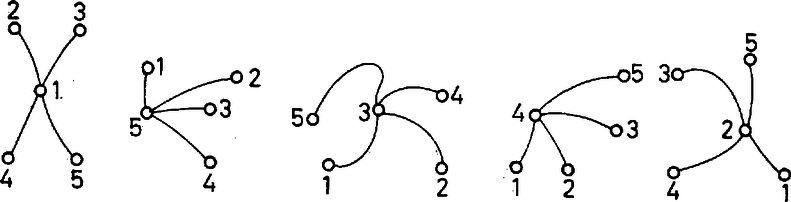
 

 

b) Most nézzük azokat a gráfokat, amelyekben 1 harmadfokú, 1 másodfokú és 3 első fokú pont van. Néhány példa: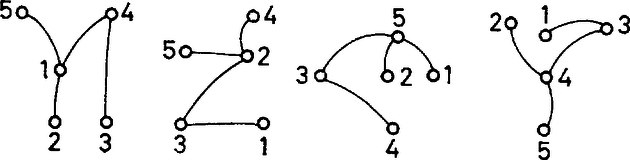
 

 

A harmadfokú pontot 5-féleképpen választhatjuk ki. A másodfokút 4-féleképpen, végül a maradék 3-ból azt, amelyik a másodfokúhoz kapcsolódik, 3-féleképpen. Az ilyen típusú gráfok száma tehát: 5⋅4⋅3=60.
c) Még az az eset lehetséges, amikor 3 másodfokú és 2 első fokú pontból áll a fa. Mit tudunk ekkor róla? Az ilyen gráf út. Az 5 pontot 5!-féleképpen rendezhetjük sorba. Két számozott gráf nem számít különbözőnek, ha ,,visszafelé'' olvassuk a számokat, de bármely pontra igaz, hogy mindkét gráfban ugyanazokkal a számokkal van összekötve. Ezért 5!2=60 különböző utat készíthetünk 5 pontból. Összesen tehát 5+60+60=125 ötszögpontú számozott fa van.
Észrevehetjük, hogy 16=42 és 125=53. Ebből azt sejthetjük, hogy n szögpontú gráf esetén valószínűleg nn-2db számozott fa van. Ezt szeretnénk bizonyítani. Kombinatorikai ismereteink alapján tudjuk, hogy az adott n különböző szám közül ‐ ismétléseket is megengedve ‐ kiválasztható (n-2) tagú számsorozatok száma éppen nn-2. Elegendő lenne tehát egy-egy értelmű megfeleltetést találni egy számozott fa és egy ilyen módon előállított (n-2) tagú számsor között.
Először próbáljunk egyértelműen hozzárendelni minden fához egy számsort! Ezt kódolásnak nevezzük.
1. Keressük meg a gráf legkisebb sorszámú első fokú tagját. Írjuk le a hozzá tartozó él másik végpontjának számát. (Ez egyértelmű, lásd az első fokú pont definícióját!)
2. A tekintett két végpont által meghatározott élt hagyjuk el. Az így nyert fára ismételten alkalmazzuk az előző módszert mindaddig, amíg a gráf éppen 2 első fokú pontból áll. Ekkorra elkészült a keresett számsor. Vizsgáljuk meg a tulajdonságait!
A kódban minden tag 1-gyel kevesebbszer szerepel, mint pontjának fokszáma, mert egy adott pont számát annyiszor írjuk le, ahányszor valamely hozzá kapcsolódó pont éppen a legkisebb első fokúvá válik, mindaddig, míg a kiszemelt pont legalább másodfokú. Amint azonban a vizsgált pont maga is első fokú lesz, akkor a hozzá kapcsolódó magasabb fokszámú pont számát írjuk a sorozatba, vagy ha a hozzá kapcsolódó pont is éppen első fokú, akkor már elkészült az előző lépésben a kód, nem írunk hozzá semmit.
Ezt a tulajdonságot felhasználva bizonyíthatjuk, hogy a kód éppen (n-2) tagú. Mivel a fa éleinek száma (n-1), és minden él pontosan két pontba fut be, a fokszámok összege a fában 2(n-1). Minden egyes pont éppen 1-gyel kevesebbszer szerepel a sorozatban, mint saját fokszáma, tehát a kód elemeinek száma pontosan a fokszámok összegének és a pontok számának különbsége, azaz 2(n-1)-n=n-2.
6. kérdés. Mi az alábbi fa kódja?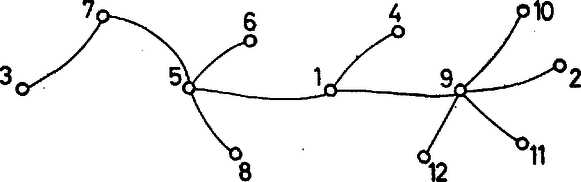
 

 

Most már a kódolás egyértelműségét bebizonyítottuk, azaz beláttuk, hogy minden fa és egy (n-2) tagú számsor között függvénykapcsolat létesíthető. Feladatunk a hozzárendelés másik irányban is fennálló egyértelműségének bizonyítása. Ezt dekódolásnak nevezzük.
Rendezzük sorba nagyság szerint a kódban nem szereplő, n-nél nem nagyobb természetes számokat. Ezek a fa első fokú pontjai. Rajzoljuk fel lépésenként a gráfot a következő módszerrel. A kódolás első lépésének megfelelően a dekódolást a legkisebb elsőfokú pont és a kód első száma közötti él berajzolásával kezdjük. Ezután hagyjuk el a kód első tagját. Ha ez éppen másodfokú pont volt (a kódban egyszer szerepelt), akkor most az első fokúak sorozatába illesztjük. Ha legalább harmadfokú volt, egyszerűen töröljük az első helyről. A berajzolt elsőfokú pontokat a későbbiekben nem vesszük figyelembe.
Mivel minden egyes él berajzolásával a két végpont még meg nem rajzolt, de az eredeti gráfban meglevő fokszáma 1-gyel csökken, az új kód a keresett fa még be nem húzott éleire mint gráfra nézve megtartja eredeti tulajdonságait, annak kódszorosa. A lépéseket addig ismételjük, míg kódunk végül egyetlen számot tartalmaz. Módszerünknek megfelelően összekötjük a legkisebb első fokú ponttal. így kódunk ,,elfogyott'', és maradt két első fokú pontunk. Ezeket összekötve megkaptuk a teljes gráfot. Mivel a kódolás és dekódolás lépésenként egyértelmű volt, így megfeleltetésünk valóban egy-egy értelmű.
Beláttuk tehát, hogy n pontú számozott fák száma nn-2.
7. kérdés. Melyik fa felel meg a 2, 7, 13, 13, 13, 1, 5, 7, 13, 13, 9, 6 számsornak?
Ugyanezt a problémát más módon is megoldhatjuk. Átkódolás:
A legkisebb első fokú pontból induljunk el a következő legkisebb felé. Írjuk sorba egymás mellé azon pontok számát, melyeken áthaladtunk. A két első fokút ne írjuk le. A bejárt élek elhagyásával keletkező gráfban keressük meg ismét a legkisebb első fokú pontot. Az előző lépésben leírt útnak biztosan van olyan pontja, ahonnan elágazik egy másik út e pont felé, hiszen a gráf összefüggő. Most csak ezt az elágazási pontot írjuk le, s utána az új útvonalon megint azokat, amelyeken áthaladtunk. Ezt az eljárást addig folytassuk, amíg vannak első fokú pontok, még leíratlan utak.
Nézzük meg, hogy melyik pontot hányszor írtuk fel. A kiinduló gráf első fokú pontjait egyszer, a többit egyszer amikor átmentünk rajta és még annyiszor, ahányszor elágazási pontként szerepelt. Amikor áthaladunk egy ponton, két élt használunk, ezért minden pontot a fokszámánál 1-gyel kevesebbszer írunk le. A kód hossza tehát most is nn-2.
Most még azt kell megnézni, hogy minden olyan (n-2) tagú sorozatnak, amelyben n-nél nem nagyobb természetes számok szerepelnek (egyszer vagy akár többször is), egyértelműen megfeleltethető egy gráf. Ehhez a következő dekódolást használjuk.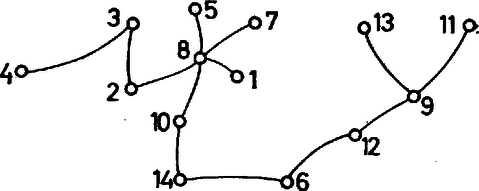
 

 

Nézzük meg, mely számok nem szerepelnek a kódban. Ezek az első fokú pontok. Válasszuk ki közülük a legkisebbet. Ezt összekötjük a kód első tagjával, azt a másodikkal és így tovább, míg egy szám meg nem ismétlődik. Az ismétlődés előtti ponthoz a következő legkisebb első fokút kapcsoljuk. Ezután menjünk az ismétlődő ponthoz, amely elágazást jelent, és rajzoljuk meg az újabb útvonalat. Ismét egy-egy értelmű megfeleltetést végeztünk tehát, mert a kódolás is, a dekódolás is lépésenként egyértelmű.
8. kérdés. Mi eszerint a következő gráf kódja?
9. kérdés. Minek a kódja a 4, 3, 10, 9, 13, 8, 8, 3, 5, 5, 5, 2 számsor?
 

Egy gyakorlati probléma
 

6. feladat. Tekintsünk egy településrendszert, ahol a falvakat utakkal szeretnénk összekötni. A településeknek a gráf pontjai, az utaknak az élek felelnek meg; feltüntetve az utak árarányát, keressük azt az úthálózatot, melyen bármely helységből eljuthatunk bármely másikba, és melynek költsége minimális.
Megoldás. Azt az összefüggő gráfot keressük tehát, amelynél az élekhez tartozó számok összege minimális. Legyen módszerünk a következő.
Húzzuk be a legkisebb számú éleket addig, míg összefüggő gráfot nem kapunk. Amint összefüggő lett a gráf, nézzük meg, van-e benne kör. Ha van, akkor minden talált körből kihúzhatunk egy élt, hiszen ekkor még összefüggő marad a gráf, viszont a számok összege csökken. Nyilvánvaló, hogy legcélszerűbb a körök legmagasabb számú éleit elhagyni. Az így kapott úthálózat lesz a minimális költségű, mivel a megépített utak száma minimális (hiszen fát kaptunk eredményül).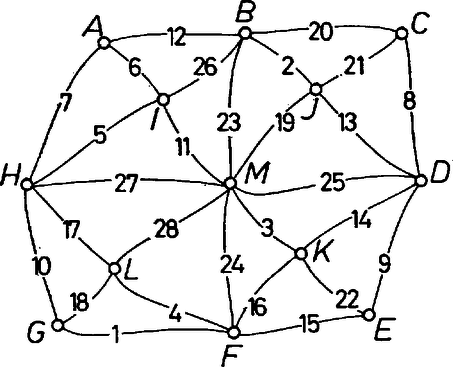
 

 

Ha bármely utat egy másikkal helyettesítenénk, a költség növekedne, mivel a be nem húzott utak vagy azok, melyekhez még nem jutottunk el az összefüggőség elérése előtt, tehát minden behúzott élnél nagyobb szám tartozik hozzájuk; vagy pedig a körök ,,kiküszöbölésénél'' hagytuk el őket, ekkor viszont megint csak felesleges lenne a csere, hiszen a ,,legdrágább'' élt hagytuk el, a kör maradék élei mind ,,olcsóbbak''.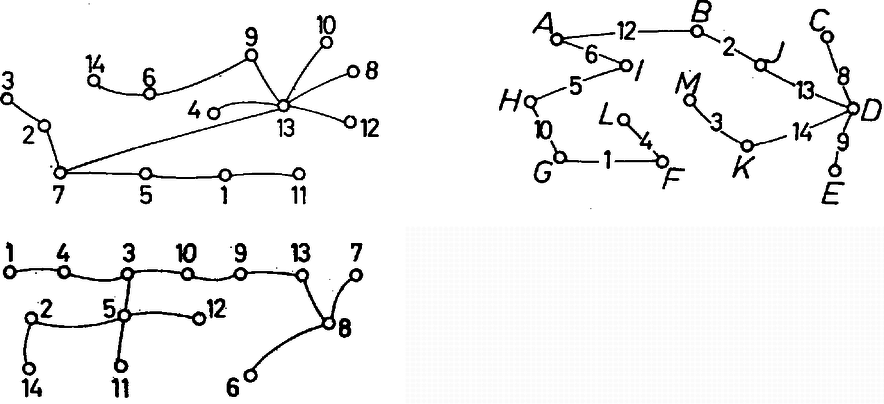
 

 

10. kérdés. Milyen úthálózatot kapunk a fenti gráfra a leírt módszer alkalmazásával?
Megoldások 1. b, c; 2. b, d; 3. c; 4. n-k; 5. e+k-n; 6. 9715551999; 7. a) ábra; 8. 8, 2, 3, 8, 8, 8, 10, 14, 6, 12, 9, 9; 9. b) ábra; 10. c) ábra.
Csoporttársaink a következők: Bánlaki József, Barabás Tibor, Fried Katalin, Kovács Gabriella, Mérő Katalin, Pallai Katalin, Szencsés László Tanárunk: Halmos Istvánné. Amit cikkünkben közöltünk, velük együtt csináltuk.