Cím: Ki mit tud, ki mit nem tud a prímszámokról?
Szerző(k):  Csirmaz László 
Füzet: 1977/január, 25. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

S. M. Ulam amerikai matematikus egy szabad délelőttjén egy kockás papírra csigavonalban felírta a természetes számsor elejét, majd a prímszámokat jelölte, úgy, ahogyan az az ábrán látható.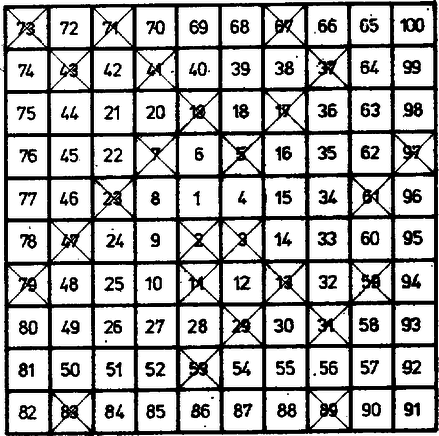

 

 

Furcsának találta, hogy a prímek mennyire kedvelik az átlós elhelyezkedést. S hogy ez mennyire így van, azt hátsó borítónkon láthatjuk, ahol egészen 90000-ig rajzoltuk fel "Ulam spirálisát''.
 

 

Hogy miért van ez? Még senki sem tudja.
A 2-nél nagyobb prímek mind páratlanok, így két egymás utáni prímszám között legalább 2 különbségnek kell lennie. Ha ez az eltérés pontosan kettő, a prímeket szomszédosaknak, ikreknek nevezzük. Ikerprímek például a 71 és 73, a 209267 és 209269 vagy az 1000000009649 és 1000000009651 számok. Akármeddig vizsgálták a prímeket, mindig újabb és újabb ikerprímek bukkantak fel. De bizonyítani, hogy végtelen sok van belőlük, még senkinek nem sikerült.
P. L. Csebisev (1821‐1894) orosz matematikus bizonyította be először, hogy minden n természetes számra n és 2n között van prím (n≥2). Ugyanerre a tételre Erdős Pál egy igen egyszerű és szellemes bizonyítást talált, amely a Középiskolai Matematikai Lapok első két kötetében olvashatók (Kalmár László: Bizonyítsuk be a Csebisev-tételt, KÖMAL 1. kötet 89., 127., 176. oldal, 2. kötet 7., 90., 121. oldal). Azt is bebizonyították, hogy elég nagy n-től n és 1,001n között is van prím, sőt minden ε>0 valós számhoz elég nagy n-re n és (1+ε)n között is található prím szám. De arra a kérdésre, hogy vajon n2 és (n+1)2 között mindig van-e prím, még mindig nem ismerjük a választ.
Tudjuk, hogy végtelen sok 2k+1 alakú prímszám van. Nem nehéz belátni azt sem, hogy végtelen sok 6k-1 alakú prím van. De vajon végtelen sok 10k+1 alakú prímszám van-e? P. G. L. Dirichlet (1805‐1859) német matematikus bizonyította be azt a nagy jelentőségű és fontos tételt, hogy ha a és b relatív prím egész számok, akkor végtelen sok a+kb alakú prímszám van. Ezt az eredményt úgy is fogalmazhatjuk, hogy minden olyan egész együtthatós első fokú polinom, melynek együtthatói relatív prímek, végtelen sok egész helyen vesz föl prímszám-értéket. Azt azonban nem tudjuk, hogy van-e egyáltalán olyan legalább másodfokú egész együtthatós polinom, ami végtelen sok egész helyen vesz föl prímszám-értéket. Viszont azt tudjuk, hogy van olyan többváltozós, egész együtthatós polinom, melynek az egész helyen felvett helyettesítési értékei közül a pozitívak éppen a prímszámokat adják ki és mindegyiket pontosan egyszer.
C. F. Gauss (1777‐1855), akit a matematika fejedelmének is neveznek, 19 éves korában oldotta meg a szabályos sokszögek szerkeszthetőségének évezredek óta vajúdó problémáját. Bizonyította, hogy pontosan azok a prímoldalú szabályos sokszögek szerkeszthetők, melyek oldalszáma 22n+1 alakban írható. Így szerkeszthető 3, 5, 17, 257 és 65537 oldalú sokszög, de nem szerkeszthető például 7, 11, 13 stb. oldalú. Szabályos három- és ötszöget szerkeszteni mindenki tud. A szabályos 17-szög szerkesztésének leírása és a szerkesztés helyességének bizonyítása úgy 3 oldalt tesz ki (lásd KÖMAL 39. kötet 25‐28. oldal). A 257 oldalúé 80 oldalt, a 65537 oldalúé pedig a göttingai egyetemen tíz nagy ládába zárva található ‐ ez utóbbira eddig még senki sem volt kíváncsi. A 22n+1 alakú prímeket Fermat-féle prímeknek nevezzük, mivel P. Fermat (1601‐1655) francia matematikus azt sejtette, hogy az összes ilyen alakú szám prím. Leonhard Euler (1707‐1783), aki Gauss mellett a 18. század másik nagy matematikusa volt, vette magának a fáradságot, hogy ellenőrizze vajon a 22n+1 sorozat ötödik eleme, 232+1=4294967297 valóban prím-e. Azt találta hogy ez a szám 641-gyel osztható, és így nem prím. Elektromos számítógépekkel egészen n=30-ig vizsgálták meg a Fermat-féle számokat, és egyetlen további prímet sem találtak a már ismerteken kívül. Van-e még a Fermat-féle számok között prím egyáltalán? Ha igen, végtelen sok-e? Ezt ma még senki sem tudja.