Kezdőlap


Cím:	1976. évi fizika OKTV feladatai
Füzet:	1976/október, 81 - 86. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai

1. Csigán átvetett fonál végein

10 kg

és

12 kg

tömegű testek lógnak. A

10 kg

tömegű testen egy rúd fekszik. A

12 kg-os

tömeget elengedve a testek elindulnak (1. ábra). Mozgás közben, a

12 kg

-os lebillenti a rudat a

10 kg

-osról. Mennyi legyen a rúd tömege, hogy a

12 kg

-os test éppen a csigához érkezzen fel ?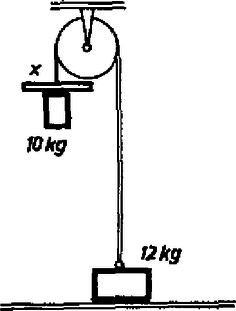

1. ábra

Megoldás. Először egyenletesen gyorsuló, azután egyenletesen lassuló mozgás következik be. A távolság felezése folytán ezek útjai egyenlők:

a_{1} t_{1}^{2} / 2 =

= a_{2} t_{2}^{2} / 2

. A gyorsuló mozgás végsebessége egyenlő a lassuló mozgás kezdősebességével:

v = a_{1} t_{1} = a_{2} t_{2}

, ha eltekintünk a rúd lebillenése során bekövetkező sebességváltozástól. Ezeket a sebességeket az utak kifejezéseibe helyettesítve:

\begin{matrix} \frac{v t_{1}}{2} = \frac{v t_{2}}{2}, \end{matrix}

amiből azonnal következik, hogy a mozgás két részének az ideje és gyorsulásainak abszolút értéke egyenlő. A kisebb tömeget

m_{a}

-val, a nagyobbat

m_{b}

-vel, a rúd tömegét

x

-szel jelölve írjuk fel a gyorsulások egyenlőségét:

\begin{matrix} \frac{m_{a} + x - m_{b}}{m_{a} + x + m_{b}} \cdot g = \frac{m_{b} - m_{a}}{m_{b} + m_{a}} \cdot g . \end{matrix}

Az egyenlet megoldása:

x = \frac{m_{b}^{2} - m_{a}^{2}}{m_{a}} = 4, 4 kg

Az egyenlet ilyen alakra is hozható:

\begin{matrix} m_{b} = \sqrt[]{m_{a} (m_{a} + x)}, \end{matrix}

tehát a nagyobb tömeg mértani középarányos a kisebb tömeg és a pálcával terhelt tömeg között

R

sugarú henger tetejéről súrlódásmentesen csúszik le egy test.

a)

Mely helyzetben lesz a gyorsulás a ,,

g

'' nehézségi gyorsulás kétharmada ?

b)

Milyen irányú ekkor a gyorsulás ?

Megoldás. Az

α

szöggel meghatározott helyzetben a gyorsulás érintőleges összetevője

g sin α

, merőleges összetevője

v^{2} / R

, ahol

v

a sebesség.
A teljes gyorsulás a két összetevőből vektoriálisan tevődik össze (2. ábra):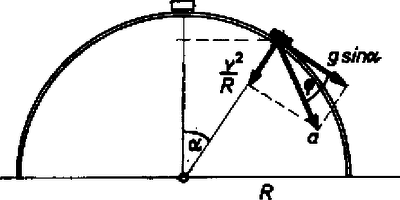

\begin{matrix} a = \sqrt[]{{(g sin α)}^{2} + {(v^{2} / R)}^{2}} . \end{matrix}

2. ábra

A sebességet mint az

α

szög függvényét az energiatételből kapjuk:

m v^{2} / 2 = m g R (1 - cos α)

, innen

v^{2} = 2 g R (1 - cos α)

. Ennek felhasználásával a gyorsulás:

\begin{matrix} a = g \sqrt[]{sin^{2} α + 4 {(1 - cos α)}^{2}} = \frac{2}{3} \cdot g . \end{matrix}

Rendezzük a kapott egyenletet:

\begin{matrix} 27 cos^{2} α - 72 cos α + 41 = 0, \end{matrix}

ennek számunkra érdekes megoldása:

\begin{matrix} cos α = (12 - \sqrt[]{21}) : 9 = 0, 8242, α = 34^{\circ} 30' . \end{matrix}

Az eredő gyorsulás az érintővel

φ

szöget zár be, erre nézve

cos φ = (g sin α) : (2 g / 3) = 1, 5 sin α = 0, 8496, φ = 31^{\circ} 48'

3. Egy

5 kg

tömegű test húzza a

3 kg

tömegű, súrlódás nélkül guruló kocsit (3. ábra). A kocsin fekvő tégla

0, 8 másodperc

múlva csúszott le a

40 cm

hosszú kocsi hátsó végén. Mennyi a csúszási súrlódási együttható a tégla és a kocsi között ? A tégla tömege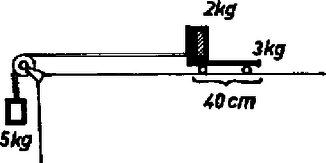

2 kg

g = 10 {m/s}^{2}

3. ábra

Megoldás. Mivel a tégla csúszik a kocsihoz képest, a tégla a kocsitól

2 kg \cdot μ g

gyorsító erőt kap és gyorsulása

μ g = a_{1}

(

μ

a súrlódási együttható).
A lelógó súly által kifejtett fonálerő

5 kg (g - a_{2})

, ez gyorsítja a

3 kg

-os kocsit és fedezi a téglát gyorsító súrlódási erőt:

\begin{matrix} 5 kg (g - a_{2}) = 3 kg a_{2} + 2 kg μ g; \end{matrix}

innen a kocsi gyorsulása:

\begin{matrix} a_{2} = \frac{5 - 2 μ}{8} \cdot g . \end{matrix}

A kocsi és tégla megtett útjainak a különbsége a kocsi 40 cm-es hossza:

\begin{matrix} \frac{a_{2}}{2} \cdot {(0, 8 s)}^{2} - \frac{a_{1}}{2} \cdot {(0, 8 s)}^{2} = 0, 4 m; \end{matrix}

a gyorsulás értékeit felhasználva:

\begin{matrix} \frac{1}{2} \cdot \frac{5 - 2 μ}{8} \cdot g \cdot {(0, 8 s)}^{2} - \frac{1}{2} \cdot μ g \cdot {(0, 8 s)}^{2} = 0, 4 m . \end{matrix}

Az egyenlet megoldása adja az eredményt:

μ = 0, 4

4. Hengeres edény szélesebb részének

5 {cm}^{2}

, keskenyebb részének

1 {cm}^{2}

a keresztmetszet-területe (4. ábra). A dugattyúk és a görgők súrlódás nélküliek. A kis dugattyút rugóval erősítettük egy cövekhez. Mit figyelhetünk meg, ha a horogra

1 kg

tömegű testet akasztunk ? A légnyomás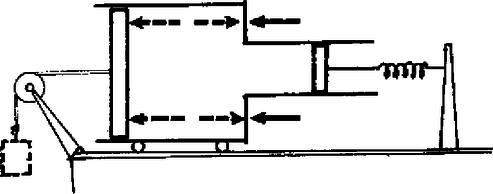

1 {kp/cm}^{2}

4. ábra

Megoldás. Kezdetben egyensúly van, a nagy dugattyút belülről és kívülről 5 kp, a kis dugattyút belülről és kívülről 1 kp, a henger jobb oldalán található

4 {cm}^{2}

területű körgyűrűt belülről és kívülről 4 kp erő nyomja. A nyomás a hengerben

1 {kp/cm}^{2}

.
Az 1 kp súlyú test horogra akasztása után a nagy dugattyút 5 kp helyett csak 4 kp erő nyomja befelé. Az elzárt levegő kiterjed, amíg nyomása

0, 8 {kp/cm}^{2}

lesz, mert ekkor nyomja a dugattyút belülről is 4 kp erő. A kis dugattyút tartó rugó megnyúlik, mert belülről

0, 8 kp

nyomja.
A

4 {cm}^{2}

területű körgyűrűt kívülről változatlanul 4 kp nyomja, de belülről csak

3, 2

kp erő, tehát az egész henger elindul balfelé. Ha a henger balfelé mozdul el, a körgyűrű elmozdulása folytán kisebbedne a belső térfogat, amelynek azonban a

0, 8 {kp/cm}^{2}

nyomás tartása miatt állandónak kell maradni. Ezért a nagy dugattyú is elindul balfelé, de a területarány következtében elmozdulása az előbb leírt helyzetéhez képest a henger elmozdulásának

80 %

-a.

A II. forduló feladatai

1. Vízszintes felületen megerősítünk egy fonalat, ezt

r = 25 cm

sugarú, m=

8 kg

tömegű henger alatt vezetjük el, azután egy ugyanolyan hengerből készült állócsigán vetjük át és a fonál szabad végére ugyancsak m=

8 kg

tömegű testet akasztunk (5. ábra). A messze levő hengerek között a fonál

60^{\circ}

-os szöget zár be a vízszintessel. Mekkora a lelógó test gyorsulása abban a pillanatban, amikor elengedjük ? (A fonál nem csúszik.)

(Dr. Wiedemann László)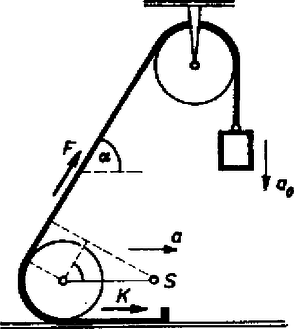

5. ábra

Megoldás. Első lépés a lelógó test

a_{0}

és a guruló henger középponti a gyorsulásának összefüggését megkeresni. Ha a henger középpontja kicsiny

s

utat tesz meg, akkor a kötélből felszabadul

s + s cos α

a darab és ez a lelógó tömeg útja:

\begin{matrix} s_{0} = s (1 + cos α) . \end{matrix}

A kicsiny

s

útszakasz megtétele alatt a gyorsulásokat állandóknak tekinthetjük, így az utak aránya a gyorsulások arányát adja meg:

\begin{matrix} a_{0} = a (1 + cos α) . \end{matrix}

Newton II. törvényét alkalmazva a henger haladó mozgására (

K

és

F

a fonálerők):

\begin{matrix} K + F cos α = m a . \end{matrix}

A henger forgására nézve:

\begin{matrix} (F - K) r = \frac{a}{r} \cdot Θ, \end{matrix}

a csiga forgására nézve:

\begin{matrix} (m g - m a_{0} - F) r = \frac{a_{0}}{r} \cdot Θ . \end{matrix}

Ugyanis sima gördülés esetében a szöggyorsulások

a / r

és

a_{0} / r, Θ

pedig a hengerek tehetetlenségi nyomatéka. Négy egyenletből álló egyenletrendszerünk megoldása a lelógó henger indulási gyorsulására vonatkozóan:

\begin{matrix} a_{0} = g \cdot \frac{{(1 + cos α)}^{2}}{(1 + Θ / m r^{2}) [1 + {(1 + cos α)}^{2}]} = \frac{6}{13} \cdot g = 0, 462 g . \end{matrix}

A másik három mennyiségre adódó megoldás:

\begin{matrix} a = g \cdot \frac{1 + cos α}{(1 + Θ / m r^{2}) [1 + {(1 + cos α)}^{2}]} = \frac{4}{13} \cdot g = 0, 308 g, \\ F = m g \cdot \frac{1}{1 + {(1 + cos α)}^{2}} = \frac{4}{13} \cdot m g = 0, 308 m g, \\ K = m g \cdot \frac{1 - Θ cos α / m r^{2}}{(1 + Θ / m r^{2}) [1 + {(1 + cos α)}^{2}]} = \frac{2}{13} \cdot m g = 0, 154 m g . \end{matrix}

2. Írjuk le a 6. ábrán látható rendszer mozgását ! Az

m_{1}

tömegű deszka és az asztal között

μ_{1}

, a deszka és az

m_{2}

tömegű tégla között

μ_{2}

a súrlódási együttható. (A csúszó és tapadási súrlódási együttható egyenlő.) Számadatok:

m_{1} = 2 kg, m_{2} = 2 kg, m_{3} = 1 kg, μ_{1} = 0, 1, μ_{2} = 0, 35

(Párkányi László)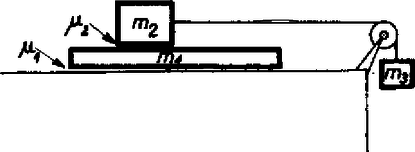

6. ábra

Megoldás. Taglalni kell, hogy a megadott számadatok: esetében milyen mozgás jön létre.
Semmi sem mozog, ha

m_{3} g < μ_{2} m_{2} g

, és egyidejűleg

m_{3} g < μ_{1} (m_{1} + m_{2}) g

. A mi számadataink mindkettőnek ellentmondanak, ez az eset nem valósul meg.
A deszka akkor mozog, ha a súrlódási erőkre vonatkozóan igaz, hogy

\begin{matrix} μ_{2} m_{2} g > μ_{1} (m_{1} + m_{2}) g . \end{matrix}

Számadataink megfelelnek ennek a feltételnek, tehát a deszka feltétlenül mozog. De az a kérdés, hogy a téglával együtt vagy külön ? Ha a deszka és a tégla külön mozognának, akkor gyorsulásaik ezek volnának:

\begin{matrix} a_{1} = \frac{μ_{2} m_{2} g - μ_{1} (m_{1} + m_{2}) g}{m_{2}} = 0, 15 g, \\ a_{2} = \frac{m_{3} g - μ_{2} m_{2} g}{m_{2} + m_{3}} = 0, 1 g . \end{matrix}

De az lehetetlen, hogy a deszka nagyobb gyorsulással mozogjon, mint a tégla. Így marad az utolsó eset: a tégla és a deszka együtt mozognak. Ebben az esetben a deszka és a tégla közös gyorsulása:

\begin{matrix} a = \frac{m_{3} - μ_{1} (m_{1} + m_{2})}{m_{1} + m_{2} + m_{3}} \cdot g = 0, 12 g . \end{matrix}

Érdekes, hogy azok a feltételek, amelyek a mozgás fajtáját döntik el, függetlenek a nehézségi gyorsulástól.

3. Elhanyagolható ellenállású anyagból készült

r

sugarú korongot vízszintes tengellyel csapágyaztunk. Tengelyén

ϱ

sugarú kis kerék van, amelyről fonálon

m

tömegű, test, lóg le (7. ábra). A tengely csapágya és a kerülethez hozzáérő csúszó érintkező közé

R

ellenállást kapcsolunk. Az egész korong vízszintes irányú

B

indukciójú mágneses térben van. Mekkora végső szögsebességre áll be a forgó korong ? Számadatok:

r = 10 cm, ϱ = 2 cm, R = 0, 01 ohm, B = 0, 2 tesla, m =

= 50 gramm

(Dr. Wiedemann László)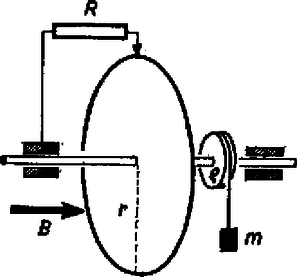

7. ábra

Megoldás. Az úgynevezett unipoláris indukcióról van szó. A korongban a tengelytől az érintkezőig a legkülönbözőbb utakon halad az áram:

I = I_{1} + I_{2} + ...

. Tekintsük az

I_{1}

áram útjának egy olyan kis darabját, amelynek a rádiusz irányába eső összetevője

Δ r

, az erre ható mágneses erő

B I_{1} Δ r

. Ennek az erőnek a forgatónyomatéka

B I_{1} r \cdot Δ r

, az egész forgatónyomaték egyetlen áramfonálnál:

0, 5 B I_{1} r^{2}

. Ugyanígy a második áramfonálnál

0, 5 B I_{2} r^{2}

, öszszegezve

0, 5 B I r^{2}

.
Az indukált elektromotoros erő

U = B r v / 2

, ahol

v

a kerületen érvényes sebességet jelenti és átlagban a középponthoz haladva a fele számítandó. A kerületi sebesség a szögsebességgel kifejezve

v = ω r

, így az indukált elektromotoros erő

U = B ω r^{2} / 2

, az áramerősség pedig

I = U / R = B ω r^{2} / (2 R)

. Az erre az áramra ható mágneses erő forgatónyomatéka

ω B^{2} r^{4} / (4 R)

. A beálló végállapot esetében ez egyenlő a lelógó súly

m g ϱ

forgatónyomatékával:

\begin{matrix} \frac{ω B^{2} r^{4}}{4 R} = m g ϱ, \end{matrix}

innen:

\begin{matrix} ω = \frac{4 m g ϱ R}{B^{2} r^{4}} . \end{matrix}

Számadatainkkal

ω = 100 s^{- 1}

A III. kísérleti forduló
A II. forduló dolgozatai alapján 24 versenyző kísérleti versenyen vett részt Budapesten az ELTE Természettudományi Karának Általános Fizikai Tanszékén. Egyrészt egy forgó szerkezet súrlódási forgatónyomatékát kellett meghatározniuk, másrészt értelmezni kellett a poláros fény témakörébe tartozó bemutatott kísérletet.

Az 1976. évi fizikai tanulmányi verseny eredménye.

A fizikából nem tagozatos tanulók versenyében:

\begin{matrix} I. díj: & Zimányi Gergely (Budapest, Fazekas M. Gimn. IV. o. t., tanára: Mihály István) . \\ II. díj: & Vankó Péter (Budapest, Móricz Zs. Gimn. III. o. t., tanára: Sikó Attiláné) . \\ III. díj: & Gulyás Mihály (Orosháza, Táncsics M. Gimn. IV. o. t., tanára: Győrös Gyula) . \end{matrix}

A további helyezettek: 4. Zsigmond Géza (Budapest, Fazekas M. Gimn. IV. o. t., Mihály István), 5. Tóth István (Tata., Eötvös J. Gimn. IV. o. t., Mészáros András), 6. Binzberger Gábor (Budapest, Móricz Zs. Gimn. IV. o. t., Széplaki Jenőné), 7. Lórántfy László (Kecskemét, Katona J. Gimn. IV. o. t., Szakács Jenő), 8. Molnár Árpád (Budapest, Fazekas M. Gimn. IV. o. t., Mihály István), 9. Harsányi Gábor (Budapest, Radnóti M. Gimn. IV. o. t., Rácz Mihály), 10. Tornóci László (Tata, Eötvös J. Gimn. IV. o. t., Mészáros András).

A fizikából tagozatos tanulók versenyében:

\begin{matrix} I. díj: & Holló Sándor (Eger, Gárdonyi G. Gimn. IV. o. t., tanára: Leitner Györgyné) . \\ II. díj: & Ambrus András (Szeged, Radnóti M. Gimn. IV. o. t., tanára: Bábitzky Edéné) . \\ III. díj: & Faragó Béla (Csongrád, Batsányi J. Gimn. IV. o. t., tanára: Szucsán András) . \end{matrix}

A további helyezettek: 4. Kovács Gábor (Budapest, Landler J. Gimn. IV. o. t., Kocsis Ferencné), 5. Tar József (Eger, Gárdonyi G. Gimn. IV. o. t., Leitner Györgyné), 6. Dávid József (Bonyhád, Petőfi S. Gimn. IV. o. t., Erdélyesi János), 7. Virosztek Attila (Szolnok, Verseghy F. Gimn. N. o. t., Sebestyén István), 8. Drankovics József (Kaposvár, Táncsics M. Gimn. IV. o. t., Gál József), 9. Földvári Csaba (Budapest, Apáczai Csere Gimn. N. o. t., Holics László), 10. Forján János (Békéscsaba, Rózsa F. Gimn. III. o. t., Uhrin János).