Kezdőlap


Cím:	1975. évi Eötvös Loránd Fizikaverseny
Füzet:	1976/február, 81 - 84. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1975. október 25-én rendezte 52. versenyét Budapesten és 8 vidéki városban az idén érettségizettek és középiskolai tanulók számára. A versenyzők 5 órai munkaidő alatt oldhatták meg a három feladatot és bármilyen segédeszközt használhattak. A versenyzők száma 367 volt. Ismertetjük a feladatokat és megoldásukat.

R = 36 cm

sugarú félhenger tetejéről egy

r = 4 cm

sugarú golyó gurul le (

1

. ábra). A súrlódási együttható

μ = 0, 4

. Hol csúszik meg a leguruló golyó?

1. ábra

Megoldás. A kis golyó helyzetét az

α

szöggel határozzuk meg (2. ábra).

2. ábra

A golyóra ható erők: súlyerő

(m g)

, súrlódási erő

(S)

és nyomóerő

(N)

. A golyó tömegközéppontja

R + r

sugarú körpályán mozog. A mozgásegyenlet a sugárirányú és érintőleges komponensekre (

v

a golyó tömegközéppontjának sebessége):

\begin{matrix} m v^{2} / (R + r) = m g cos α - N, & (1) \\ m a = m g sin α - S . & (2) \end{matrix}

A forgó mozgás egyenlete (

Θ

a golyó tehetetlenségi nyomatéka,

β

a szöggyorsulása):

\begin{matrix} Θ β = S \cdot r . \end{matrix}

(3)

A sebességet az energiatételből kaphatjuk meg (a megcsúszásig nincs súrlódási energiaveszteség;

ω

a szögsebesség):

\begin{matrix} m g (R + r) (1 - cos α) = (1 / 2) m v^{2} + (1 / 2) Θ ω^{2} . \end{matrix}

(4)

A csúszásmentes gördülés feltételei (részletesebben 1. KML 47(1973) 23.):

\begin{matrix} a = r \cdot β, & (5) \\ v = r \cdot ω . & (6) \end{matrix}

A megcsúszás határán

\begin{matrix} S = μ N . \end{matrix}

(7)

A kapott hétismeretlenes egyenletrendszerből a megcsúszás helyzetét jellemző

α

szögre a következő egyenletet kapjuk:

\begin{matrix} (3 + \frac{Θ}{m r^{2}}) \cdot cos α - 2 = \frac{1}{μ} \cdot \frac{Θ}{m r^{2}} \cdot sin α . \end{matrix}

Igen figyelemre méltó, hogy az eredmény teljesen független a sugaraktól, még azok aránya sem szerepel az eredményben. Tehát egy labdáról a sörétszem, vagy a sörétszemről a labda leguruláskor ugyanazon szöghelyzetben csúszik meg. Gömb esetében

Θ / m r^{2} = 0, 4

, ekkor:

\begin{matrix} 3, 4 cos α - 2 = \frac{0, 4}{μ} \sqrt[]{1 - cos^{2} α} . \end{matrix}

Feladatunkban

μ = 0, 4

, ezért az egyenlet végső alakja:

\begin{matrix} 12, 56 cos^{2} α - 13, 6 cos α + 3 = 0. \end{matrix}

Ennek megoldása

cos α = 0, 7743

α = 39, 25^{\circ}

2. A

3

. ábra szerinti vékony csőben higany van, az elzárt légoszlop hossza

L

, a higanyszintek különbsége

l

. Mi történik, ha a higanyszintek véletlen lökés folytán kissé elmozdulnak?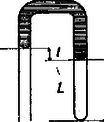

3. ábra

Megoldás. A rendszer stabilitását kell megvizsgálnunk. Legyen a külső légnyomás

p_{0}

. A lezárt csőben a határfelületen az elzárt levegő

p_{k i}

nyomással nyomja a higanyt felfelé, a lefelé ható nyomás az elmozdulás előtt

p_{b e} = p_{0} + l γ_{H g}

.
Mozduljon el a határfelszín

x

távolsággal felfelé (4. ábra).

4. ábra

Ekkor a befelé szorító nyomás: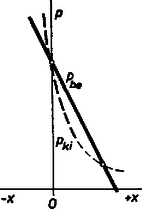

\begin{matrix} p_{b e} = p_{0} + (l - 2 x) γ_{H g}, \end{matrix}

tehát lineárisan csökkenő (5. ábra).

5. ábra

Meg kell vizsgálnunk, hogyan alakul ekkor az elzárt levegő

p_{k i}

nyomása. A Boyle‐Mariotte törvény szerint:

\begin{matrix} (p_{0} + l γ_{H g}) L = p_{k i} (L + x), \end{matrix}

vagyis

\begin{matrix} p_{k i} = \frac{(p_{0} + l γ_{H g}) L}{L + x} . \end{matrix}

A levegő nyomása hiperbolafüggvény szerint csökken. A stabilitást az határozza meg, hogy

p_{b e}

vagy

p_{k i}

csökken-e rohamosabban az

x = 0

érték környezetében.
A

p_{k i}

differenciálhányadosa:

\begin{matrix} \frac{d p_{k i}}{d x} = - \frac{(p_{0} + l γ_{H g}) L}{{(L + x)}^{2}} . \end{matrix}

x = 0

esetében a differenciálhányados

- (p_{0} + l γ_{H g} / L

. A stabilitás feltétele, hogy ennek abszolút értéke nagyobb legyen, mint 2:

\begin{matrix} \frac{p_{0} + l γ_{H g}}{L} > 2, \end{matrix}

vagy más alakban

\begin{matrix} L < \frac{p_{0} + l γ_{H g}}{2} . \end{matrix}

Stabilis egyensúlyi helyzet esetében van a hiperbola és egyenes között egy másik metszéspont is, amely labilis egyensúlyt jelent. Ha a higany rezgést végez stabilis egyensúlyi helyzete körül, az amplitudónak nem szabad akkorának lennie, hogy idáig eljusson. Viszont, ha a kezdeti egyensúlyi helyzet labilis, akkor erős összenyomással, negatív

x

-nél el lehet jutni egy stabilis egyensúlyhoz.
A 6. ábra az egyensúlyviszonyok áttekintésére szolgál.

6. ábra

Ezen az ábrán az (1,1) pontban átmenő, 2-es iránytangensű egyenes választja szét a stabilis és labilis egyensúlyi helyzeteket.

3. Közös, teljesen zárt vasmagon (

7

. ábra) ugyanazon huzalból készült

200

300

és

400

menetes tekercsek vannak. Hogyan kell ezeket összekapcsolni, hogy a keletkezett tekercsrendszer önindukciós együtthatója a lehető legkisebb legyen?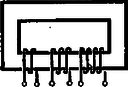

7. ábra

Megoldás. Ha a tekercsek távol vannak és semmi csatolás sincs közöttük, akkor soros és párhuzamos kapcsolási törvényük olyan, mint az ellenállásoké. Itt azonban szoros csatolást tételeztünk fel, vagyis a vasmagban levő erővonalszám valamennyi tekercs számára közös.

Egyetlen tekercs önindukciós együtthatója arányos az

n

menetszám négyzetével:

L = n^{2} k

. Soros kapcsolású tekercs eredő induktivitása aszerint, hogy a menetirány egyező vagy ellentétes:

{(n_{1} + n_{2})}^{2}

k

, illetve

{(n_{1} - n_{2})}^{2}

k

. Eszerint soros kapcsolás esetében a

200 + 300 - 400

összeállítás adja a legkisebb induktivitást.

Bonyolultabb és meglepőbb a párhuzamos kapcsolás esete. Ha egy ohmos ellenállás nélküli tekercsre állandó feszültségkülönbséget kapcsolunk, akkor az áramerősség az idővel egyenes arányban növekszik és a növekedés sebessége arányos az alkalmazott feszültségkülönbséggel: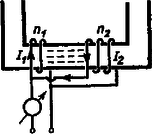

\begin{matrix} U = L \cdot d I / d t . \end{matrix}

Az arányossági szorzó az induktivitás:

\begin{matrix} L = U : (d I / d t) . \end{matrix}

Kapcsoljunk párhuzamosan

n_{1}

és

n_{2}

menetszámú tekercseket ugyanazon vasmagra, egyező menetiránnyal (8. ábra).

8. ábra

A vasmagban levő indukcióvonalak száma (az arányossági szorzót elhagyva):

\begin{matrix} N = n_{1} I_{1} + n_{2} I_{2} . \end{matrix}

Az erővonalszám változásának sebessége:

\begin{matrix} \frac{d N}{d t} = n_{1} \frac{d I_{1}}{d t} + n_{2} \frac{d I_{2}}{d t} . \end{matrix}

Az első tekercsben indukált feszültség:

\begin{matrix} U_{1} = k n_{1} \cdot \frac{d N}{d t} = k n_{1}^{2} \frac{d I_{1}}{d t} + k n_{1} n_{2} \frac{d I_{2}}{d t} . \end{matrix}

Hasonlóan a második tekercsben indukált feszültség:

\begin{matrix} U_{2} = k n_{2} \cdot \frac{d N}{d t} = k n_{1} n_{2} \frac{d I_{1}}{d t} + k n_{2}^{2} \frac{d I_{2}}{d t} . \end{matrix}

A tekercsvégek össze vannak kötve, ezért a fenti két feszültség egyenlő:

U_{1} = U_{2}

. Az egyenlőséget rendezve:

\begin{matrix} n_{1} (n_{1} - n_{2}) \frac{d I_{1}}{d t} = - n_{2} (n_{1} - n_{2}) \frac{d I_{2}}{d t}, \\ n_{1} d I_{1} = - n_{2} d I_{2}, \\ n_{1} d I_{1} + n_{2} d I_{2} = d N = 0. \end{matrix}

Vagyis az erővonalak száma változatlan marad. De akkor a közös

U_{1} = U_{2}

feszültség is nulla. Az induktivitást definiáló egyenletünk szerint az önindukciós együttható nulla. Ez ellentétes menetiránynál is így van. Az

n_{2}

menetszámú tekercsben indukált áram az eredeti árammal egyező irányban folyik bele az

n_{1}

-es tekercsbe. A valóságban a csatolás sohasem teljes és ez a furcsa eset tökéletesen nem alakul ki.

A verseny eredménye: A versenyen az első díjat nem osztották ki. Két egyenlő helyezésű II. díjat nyert Szép Jenő honvéd (a budapesti Veres Pálné Gimnáziumban érettségizett Kishonti Istvánné tanítványaként) és Zimányi Gergely (Bp., Fazekas M. Gyak. Gimn., IV. o. t., tanára: Mihály István). III. díjat nyert Virosztek Attila (Szolnok, Verseghy F. Gimn., IV. o. t., tanára: Sebestyén István). Dicséretet kaptak jutalommal Gulyás Mihály (Orosháza, Táncsics M. Gimn., IV. o. t., tanára: Györös Gyula), Molnár László (Bp., Veres Pálné Gimn., IV. o. t., tanára: Pápai Tiborné), Nagy Tamás (Debrecen, Kossuth L. Gimn., IV. o. t., tanára: Farkas József) és Zsigmond Géza (Bp., Fazekas M. Gyak. Gimn., IV. o. t., tanára Mihály István).