|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A Matematika Tanítása című folyóirat 1974. évi 6. és 1975. évi 1. számában cikk jelent meg "A Középiskolai Matematikai Lapokról'' címmel. Nincs szándékomban az ott leírtakkal részletesen foglalkozni, de hadd ragadjak ki belőle egy idézetet: "A szerkesztőség szeretne a lapban közvetlenebb kapcsolatot is kialakítani az iskolákkal.'' A kapcsolat egyik megvalósítási formája lehetne olyan beszámolók közlése, amely valamely iskolában folyó matematika-életet ismertetné, vagy bemutatná egy-egy szakkör munkáját.
Ezért gondoltam arra, hogy ízelítőt adok az általam vezetett szakkör munkájából, anélkül, hogy a szakkör egész munkáját ismertetném, mely csak egy része azoknak a törekvéseknek, amelyek iskolánkban ‐ a miskolci Földes Ferenc Gimnáziumban ‐ a matematika iránt érdeklődő tanulók tehetségének kibontakoztatására irányulnak.
A szakkör tagjai matematika tagozatos IV. osztályos tanulók, akik a Középiskolai Matematikai Lapok feladatainak rendszeres megoldói. Így természetes, hogy a szakköri összejöveteleken (a beküldési határidő elmúltával) a KÖMAL feladatok megoldását megbeszéljük, értékeljük a különböző megoldásokat. Gyakran fűzünk ezekhez megjegyzéseket, kiegészítéseket vagy új kérdéseket vetünk fel, amelyekre igyekszünk választ is adni. Így többször előfordult, hogy a szóban forgó feladathoz hasonló vagy új feladat született.
A szakköri tagok általános iskolai szakköröket is vezetnek, olyan 8. osztályos tanulóknak, akik iskolánkban matematika tagozaton szeretnék folytatni tanulmányaikat. Az általános iskolai tanulókkal való foglalkozásra feladatgyűjtéssel készülünk. Forrásként elsősorban a KÖMAL-ban megjelent feladatokat használjuk fel, bizonyos könnyítésekkel, változtatásokkal.
E tevékenységi formák vezettek arra a gondolatra, hogy félretéve a szakköri munka hagyományos feladatmegoldó formaját; közös munkával feladatokat készítsünk.
A következő ismert feladatból indultunk ki:
I. feladat. Adott egy -nál kisebb szög és a szögtartomány egy belső pontja. Tekintsük azokat a háromszögeket, amelyeket a ponton átmenő egyenesek vágnak le a szögtartományból. Hogyan kell az egyenest megválaszt tani, hogy a háromszög területe a lehető legkisebb legyen?
Legyen a szög csúcsa , és messe a ponton átmenő valamely egyenes (szelő) a szög szárait olyan és pontokban, melyre .
Ha pl. (1. ábra), akkor tükrözzük az egyenest a pontra, a kapott egyenesnek a , ill. egyenessel való metszéspontját jelölje , ill. , a és egyenesek metszéspontja pedig legyen . Mivel tükörképe a pontra az pont, így , tehát a szakasz belső pontja. A és a háromszögek egybevágók, területük egyenlő, ebből következik, hogy az négyszög területe egyenlő az háromszög területével, tehát az háromszög területe a háromszög területével nagyobb az háromszög területénél. Ez a "területtöbblet'' csak akkor hiányzik, ha , azaz a egyenes egybeesik a egyenessel. Eszerint a ponton átmenő szelők közül az vágja le a minimális területű háromszöget, amelynek a szárak közé eső , szakaszát a pont felezi.
Keressük más megoldását a feladatnak. Tekintsük az paralelogrammát, melyet úgy kaptunk, hogy a ponton keresztül párhuzamost húztunk a szög száraival. ( az , az szakasz pontja.) A paralelogramma oldalait jelöljük -val és -vel (2. ábra).
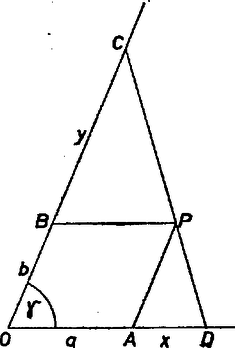 2. ábra
Legyen továbbá , . Az háromszög kétszeres területe Figyelembe véve az és a háromszögek hasonlóságát: Innen -t kifejezve és a fenti képletbe helyettesítve a | | (2) |
egyváltozós függvényt kapjuk. (Az egyszerűség kedvéért a bal oldalt -vel jelöltük.)
A függvény értelmezési tartománya a pozitív számok összessége, hiszen a ponton átmenő szelő akkor és csak akkor metszi a szög mindkét szárát, ha , azaz .
A (2) függvény ábráját vázlatosan meg is rajzolhatjuk a derékszögű koordinátarendszerben a ismert függvények grafikus összadása révén (3. ábra).
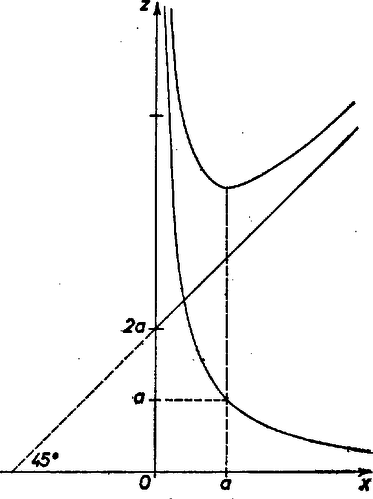 3. ábra
A (2) függvény szélsőértékének meghatározásához vegyük fÍgyelembe, hogy az összegben a két tag szorzata , amely állandó, ezért az összeg akkor a legkisebb, ha vagyis .
Ekkor az háromszögben az szakasz középvonal, tehát a feladat megoldását illetően ugyanazt állapíthatjuk meg, mint az előbbi megoldásban.
Megjegyzések: A (2) függvény legkisebb értéke helyettesítéssel: Mivel a függvény folytonos, (folytonos függvények összege is ilyen) és | |
a függvény értékkészlete a -nál nem kisebb számok összessége, és minden értéket nyilván két (különböző) helyen vesz föl. (Ezek a tulajdonságok szemléletesen is tapasztalhatók a szelő pont körüli forgatásával.)
Az I. feladat megoldása egy szakköri foglalkozáson szerepelt. A szakköri tagok ezek után azt a házi feladatot kapták, hogy a feladathoz kapcsolódó problémákon gondolkozzanak, hasonló feladatokat készítsenek, és ezeket lehetőleg oldják is meg. Néhányan rögtön "vették a lapot'', sejtésük szerint pl. a legkisebb kerületű háromszög is létezik, hiszen az távolság növelésével a kerület tetszőlegesen nagy lehet. Ugyanez elmondható az összegről vagy a oldalról is.
A későbbiek során kiderült, hogy ezek a megjegyzések döntően befolyásolták az otthoni munkát, mások területtel kapcsolatos problémákon is törték a fejüket. Végeredményben a következő három foglalkozás "terméseként'' közös munkával az alábbi feladatok készültek.
II. feladat. Adott az háromszög, és oldalának egy pontja. Szerkesszünk a ponton át olyan egyenest, amely az szög tartományából az háromszöggel egyenlő területű háromszöget vág le.
(A feladat készítésében közrejátszott az az észrevétel, hogy az I. feladatban adott területhez két szelő is tartozik, és az egyik ismeretében kell megszerkeszteni a másikat.)
A feladatban előírt követelménynek nyilván az szelő is eleget tesz. Legyen egy másik megoldás a (4. ábra).
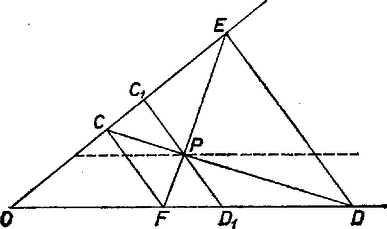 4. ábra
Az és háromszögek területének egyenlőségéből következik, hogy a és háromszögek is egyenlő területűek. Ez viszont csak úgy lehetséges, ha a közös oldalhoz tartozó magasságuk megegyezik, azaz párhuzamos -vel. Tehát szerkesztendő a trapéz. Ismert trapéztulajdonság, hogy az átlók metszéspontján a párhuzamos oldalakkal szerkesztett párhuzamos szakaszt az átlók metszéspontja felezi. (Lásd: Geometriai feladatok gyűjteménye című középiskolai segédkönyv I. kötetének 1244. feladatát.) Eszerint a szóban forgó szakasz az I. feladatban megszerkesztett szakasz. Az ill. ponton átmenő, a egyenessel párhuzamos egyenesek pedig kimetszik a szög száraiból a ill. pontokat. Természetesen az elmondottak csak arra az esetre vonatkoznak, ha . (Ha az oldal felezőpontja, akkor a keresett egyenes azonos az -el.)
A 4. ábra alaposabb tanulmányozása közben adódott a következő gondolat:
a) Rögzítsük a és pontokat, és az , pontokra pedig azt a megszorítást tegyük, hogy a szög másik szárán mozogjanak, de úgy, hogy az és háromszögek területei egyenlők legyenek. Mi az és egyenesek metszéspontjának a mértani helye?
Az ábrából egyszerűen kiolvasható, hogy Tehát a pont a szakaszt ‐ melynek végpontja az egyik rögzített pontja, a pont pedig a másik szárat futja be ‐ adott arányban osztja. Ebből következik, hogy a mértani hely az utóbbi szárral párhuzamos félegyenes, kizárva a egyenesre illeszkedő végpontját.
Ezt követően a foglalkozáson igen termékeny pillanatok következtek. Az egyik tanuló a problémát általánosította. Szövege a következő volt:
b) A területek egyenlőségéből következik, hogy az és távolságok aránya adott. Tehát az és pontokra szabjuk azt a feltételt, hogy az adott szám legyen. Természetesen így az négyszög nem feltétlenül trapéz. Keressük az és átlók metszéspontjának a mértani helyét. c) Valaki az a) feladatot úgy módosította, hogy a , pontok helyett a , pontokat rögzítsük.
A változtatásokat elfogadtuk, de a problémák tárgyalására nem tértünk ki, mert csak egy feladat megoldására volt már idő, és volt még egy korábbi javaslat is, éspedig az, hogy a II. feladatban a szerkesztendő egyenesnek ne egy pontját , hanem az irányát adjuk meg. Tehát:
III. feladat. Adott az háromszög és vele egy síkban az egyenes. Szerkesztendő az egyenessel párhuzamos szelő, amely az szög tartományából az háromszöggel egyenlő területű háromszöget vág le.
Az egyenest önmagával párhuzamosan mozgatva észrevehetjük, hogy a feladatnak legfeljebb egy megoldása lehet. (Nincs megoldás, hogyha az ponton át az egyenessel párhuzamosan haladó egyenesnek és az oldalnak van közös pontja.)
Legyen a keresett egyenes a , és az egyenesnek az a pontja, melyre (5. ábra).
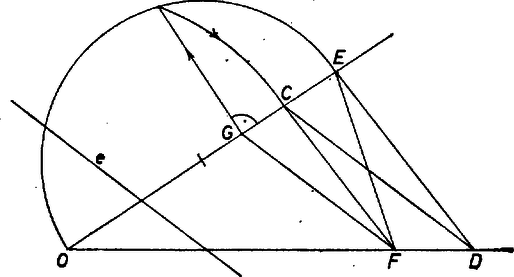 5. ábra
A és egyenesek párhuzamosak, így az és háromszögek hasonlóságából: Hasonlók azonban az és háromszögek is, tehát A két aránypárból vagyis az szakasz az és ismert távolságok mértani középarányosa. Tehát a pont szerkeszthető (pl. a befogótétel alkalmazásával).
A foglalkozás végén megállapodtunk, hogy legközelebb az I. feladathoz kapcsolódó szélsőérték-feladatokat próbálunk készíteni, erre készüljenek. Ha nehézség adódna, az adatokon "könnyítsenek''. (Közbeszólások: legyen , vagy ; előbbi helyes, az választás pedig már túlzás, hiszen ekkor a "minimum-háromszögek'' várhatóan egybeeső, egyenlő szárú háromszögek lesznek.)
Legkönnyebbnek az összeg vizsgálata bizonyult. A feladat pontos szövege a következő:
IV. feladat. Adott egy -nál kisebb szög és a szögtartomány egy belső pontja. Szerkesszük meg a ponton átmenő egyenest úgy, hogy a szög száraiból az egyenessel lemetszett két szakasz összege a lehető legkisebb legyen.
Legyen a ponton átmenő valamely egyenes a (2. ábra). Tekintettel arra, hogy az (1) összefüggés szerint az szorzat állandó, az összeg akkor a legkisebb, ha . Tehát a feladat követelményének eleget tevő szelőt úgy kell megválasztani, hogy az paralelogramma , ill. oldalának a meghosszabbításából egyenlő , ill. szakaszokat vágjon le. E szakaszok közös hossza az (1) összefüggés szerint az és távolságok mértani középarányosa, tehát Így a szerkesztés egyszerű módon elvégezhető.
A történeti hűség kedvéért meg kell említenem, hogy olyan elgondolás is akadt, amelyből nem tudtunk "értelmes dolgot kihozni''. Ugyanis észrevettük, hogy az I., ill. IV. feladatban tulajdonképpen az és szakaszok mértani, ill. számtani közepének a minimumát határoztuk meg. Miért ne foglalkozhatnánk e két szakasz harmonikus közepének, a törtnek, egyszerűbben a összegnek a változásával?
Az (1) összefüggés alkalmazásával: | |
Különböztessünk meg két esetet. Ha , feltehető, hogy , ekkor szélsőérték nincs, hiszen az változónak szigorúan monoton csökkenő függvénye. Ha pedig , azaz a szögfelező egyenesén van, akkor az és távolságok reciprokértékeinek összege állandó. (Többen jelezték, hogy az utóbbi ismerősnek tűnik.)
V. feladat. Egészítsük ki a összeget a szakasszal, és határozzuk meg a legkisebb kerületű háromszöget. (Ideiglenesen a "határozzuk'' szót használjuk, a megoldás végén derül ki, hogy felcserélhetjük-e "szerkesszük'' kifejezéssel.)
Némi kísérletezés után a feladat megoldását elég nehéznek találtuk. Könynyítésül legyen az adott szög derékszög. Jelölje az és egy (tetszőleges) egyenes hajlásszögét (6. ábra).
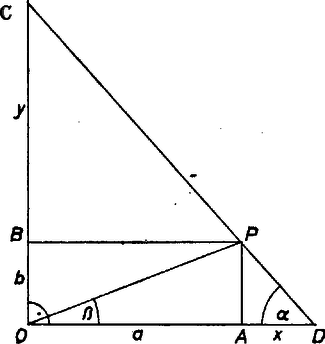 6. ábra
A háromszög kerületének változását vizsgálva elegendő nyilván csak a összegre szorítkozni.
A 6. ábra felhasználásával | |
Az szerinti derivált zérushelyét keresve, az | |
egyenlethez jutunk. Ebből átalakítások után | |
tehát Osszuk végig az egyenletet -tel, és jelölje azt a hegyesszöget (6. ábra), amelyre Ezek felhasználásával egyenletünk: Feltehető, hogy . Így a bal oldal -nál kisebb nem negatív szám, és pontosan egy olyan hegyesszög található, amely az (5) egyenletet kielégíti. Ez azonban a feladat megoldását jelentő minimumhely is. (A szélsőérték létezik, éspedig minimum, hiszen szögekre az nevezője pozitív, a számláló pedig szigorúan monoton nő és így az helyen negatívból megy pozitívba.)
Az (5) egyenlet módot ad minimális kerületű háromszög szerkesztésére. Ha , , ha pedig , akkor tekintsük azt a pontot, amely a szakasz, mint átmérő fölé rajzolt félkör és a középpontú, sugarú kör metszéspontja (7. ábra).
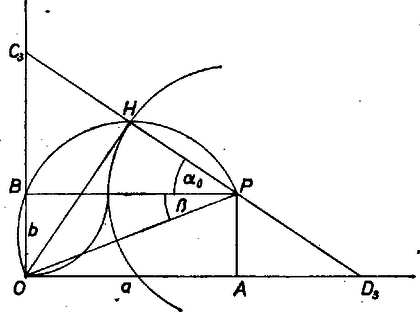 7. ábra
Az derékszögű háromszögre (5) nyilvánvalóan igaz, tehát a egyenes azonos a egyenessel.
Miután szerkesztési eljárást találtunk a keresett egyenes meghatározására, az V. feladat ‐ a IV. szövegét alapul véve ‐ a szükséges változtatásokkal pontosan megfogalmazható.
Ha a feladatban a egyenesnek csak a meghatározását kívánjuk, akkor természetesen az (5) megadásával a feladatot megoldottuk. Egy későbben felmerülő probléma azonban azt kívánta, hogy utólag számítsuk ki az távolságot. Tulajdonképpen a (4) egyenletet kielégítő hegyesszög tangensét kell kifejezni az , paraméterekkel.
Használjuk fel a | |
összefüggéseket a jelölés bevezetésével. Helyettesítés és átalakítás után a (4) egyenlet: és ebből miatt Tehát | |
VI. feladat. Maradjon az adott szög továbbra is derékszög, és a ponton átmenő egyenesek közül határozzuk meg azt, amelynek a szárak közé eső szakasza a lehető legkisebb.
Tekintsük a 6. ábrát és az (1) összefüggést: A műveletek elvégzése és rendezés után: | |
A jobb oldalon álló bármelyik zárójeles kifejezésben a három tag szorzata állandó, és így az összeg külön-külön akkor a legkisebb, ha a tagok egyenlők, tehát az egyenlőségek fennállása mellett. Mindkét egyenletből Szerencsés eset, hogy a két minimumhely egyenlő, hiszen így bizonyos, hogy a kapott érték az összegfüggvény minimumhelye is. (Az igazság az, hogy a "társaság'' az otthoni munka során a differenciálszámítás alkalmazásával próbált eredményt elérni. Valakinek sikerült a kapott harmadfokú egyenlet gyökét meghatározni, és ennek ismeretében "jöttünk rá'' a fenti módszerre.)
Tehát ‐ tekintettel még az (1) összefüggésre ‐ a minimális átfogójú derékszögű háromszög befogói: | | (5) |
Keressünk összefüggést a szakasz hosszára. | |
A jobb oldal kéttagú összeg köbe, tehát
Most a feladat szövegében a szerkesztés szót nem szerencsés szerepeltetni, ugyanis a , pontok szerkesztése ‐ itt nem részletezhető okok miatt ─nem hajtható végre. (Kivéve természetesen azokat az eseteket, amikor az és távolságokat szándékosan úgy választjuk, hogy szerkeszthető legyen pl. , .) Ha az olvasó ismeri a kocka megkettőzésének problémáját, akkor elegendő pl. azt észrevenni, hogy választással .
Több javaslat is elhangzott a feladat végső szövegezését illetően, végül is a következőt fogadtuk el, azzal az indokkal, hogy ebben már ne legyen háromszög, és leplezzük le a feladat szélsőérték jellegét:
A téglalap , ill. oldalát hosszabítsuk meg az , ill. ponton túl. Messe a ponton átmenő egyenes a meghosszabbításokat az , ill. pontban. Igazoljuk, hogy
Az ezután következő események is érdekesek voltak. Megunva a sok szélsőérték-feladat gyártását, az a kívánság merült föl, hogy jó lenne a négy feladat (I., IV., V., VI.,) megoldása során kapott "minimum-háromszögeket'' egy ábrán látni, természetesen legyen mindenütt . Kiváló ötlet, de mindenekelőtt el kellett dönteni azt, hogy pl. a , , , csúcsok hogyan következnek egymás után.
Rendelkezésünkre állnak az távolságok az , paraméterekkel kifejezve, (az -at ekkor számítottuk ki): Az nyilvánvaló, hogy ha , a második kisebb, mint az első. Kiderült azonban, hogy ez a láncolat folytatódik, tehát a fenti sorozat szigorúan monoton csökkenő. (Győződjék meg róla az Olvasó is!) Ezek után készült a 8. ábra.
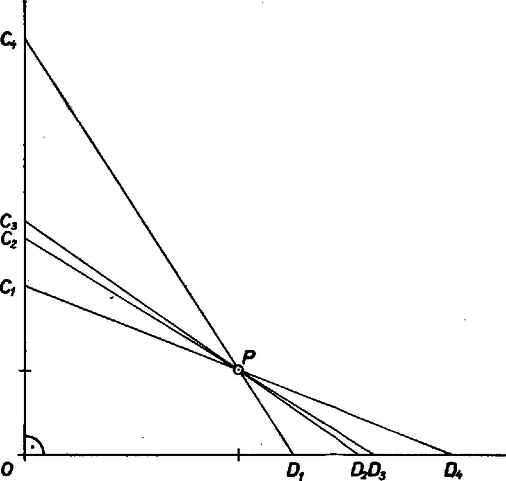 8. ábra
Valaki azt kérdezte, hogy vajon igaz-e, hogy a szakasz a legkisebbek közül is a legkisebb? Persze, a kérdés felvetése így nem helyes, inkább csak szójáték, azonban mindenki értette. Tehát ellenőrizzük a | |
egyenlőtlenségek helyességét, az utolsót az Olvasóra hagyva.
Az I. feladat megoldásából tudjuk, hogy Felhasználva (6)-ot, igazolnunk kell, hogy Ebből , helyettesítéssel adódik, hogy a jól ismert köbös és számtani közép közötti egyenlőtlenségről van szó. Ha az olvasó nem ismeri, emelje mindkét oldalt köbre, ossza végig az egyenlőtlenséget -nal , és akkor már egyszerűen kapja az egyenlőtlenséget.
A igazolása már több gondot jelent. Emeljük mindkét oldalt -ik hatványra, és mindkét oldalt fejezzük ki az , paraméterekkel, felhasználva a (3) és (6) képleteket. Rövid számítás után, adódik az alábbi egyenlőtlenség: Próbáljuk bizonyítani, egyúttal készítsünk belőle új feladatot. Hogy a gyökjelektől megszabaduljunk, emeljük mindkét oldalt köbre, és vezessük be az , jelölést.
VII. feladat. Igazoljuk, hogy a pozitív és számokra | | (7) |
Ekvivalens átalakítások után | |
A bal oldal esetén zérus, tehát kiemelhető: | |
Ismét kiemelhető , és így az | | (8) |
alakot kapjuk, amely pozitív , számpárokra nyilván igaz. Egyenlőséggé akkor és csak akkor válik ‐ a pozitív számok körében ‐ , ha .
Nehezebb feladat az összes olyan , számpár meghatározása, amelyre a (7) egyenlőtlenség teljesül. Ha , akkor az egyenlőtlenség fennáll, hiszen ekkor , vagy pedig és megegyező előjelű. Bizonyítani fogjuk, hogy más esetben nem igaz. Ehhez elegendő belátni, hogy a (8) alakban az utolsó tényező pozitív.
Írjuk ezt a tényezőt a következő módon: | | (9) |
Tehát legyenek és ellenkező előjelűek, és tekintsük a összeget. A két tag szorzata , tehát állandó, és így az összeg akkor a legkisebb, ha a két tag egyenlő. Mivel azonban pozitív szám csak akkor lehet egyenlő a reciprokával, ha a szám (és a reciproka is) , az összeg legkisebb értéke , azaz ebből tehát Eszerint a (9) valóban pozitív.
Végeredményben azt mondhatjuk, hogy (7) ekvivalens az egyenlőtlenséggel.
Már be is fejezem a "rövid'' beszámolót. Miután az Olvasó végigtanulmányozta a cikket (ha csak nem a végével kezdte), elhiszi, hogy a tanulók ezt a tevékenységet nagy kedvvel, buzgalommal, gyakran szócsaták kíséretében végezték. Mondhatja valaki, hogy tagozatos osztályról lévén szó, természetes, hogy a matematikát mindig és bármilyen mennyiségben lelkesedéssel művelik. Egyáltalán nem természetes. Ezek a tanulók középiskolai tanulmányaik során elég sok feladatot megoldottak, a feladatmegoldás egyhangú taposómalmában olykor el is fáradtak, és ez a változás számunkra is új színt jelentett.
Sokan a matematikát bonyolultnak, érthetetlennek, és ami a legnagyobb baj, algoritmikusnak tartják. Az is, ha nem tudunk megszabadulni a sablonoktól, csak tételekben, bizonyításokban gondolkodunk, és türelmetlenül, mindenáron a feladatmegoldói repertoár bővítésére törekszünk. Természetesen a készségek megszerzése is nagyon fontos, az egyszer megtanult és bevált szabályt, mozdulatot, módszert szabad többször is megismételni. Azonban a matematika elsajátításának fő mozgatója az érdeklődés fenntartása, a felfedezés öröme, a sikerélmény, ahogy mondani szokás, az ehhez vezető út pedig az önállóság, aktivitás, a tevékenységi formák helyes váltogatása, a játéktól a megfeszített munkáig.
Ha a pozitív és számok úgy változnak, hogy a szorzat állandó, a
azonosságból következően a összeg akkor a legkisebb, ha
Hasonló megállapítást tehetünk a , , pozitív számokra a
| |
azonosság felhasználásával.
Bizonyítás nélkül közöljük a következő deriválási szabályokat:
| |
|
 PDF | MathML
PDF | MathML