Kezdőlap


Cím:	Az 1975. évi (8.) Nemzetközi Fizikai Diákolimpia feladatai
Füzet:	1975/november, 161 - 166. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Egy rúd $ω$ állandó szögsebességgel forog egy függőleges tengelyhez rögzítve. A rúd a függőleges tengellyel $(90^{\circ} - α)$ szöget zár be $(1. ábra)$ . A rúdon egy $m$ tömegű test csúszhat, a csúszási súrlódási együttható $μ$ . Mi a feltétele annak, hogy forgás közben a test a rúd ugyanazon a helyén maradjon?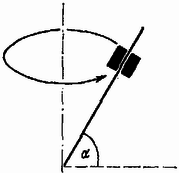

1. ábra

Megoldás. A test legyen

L

távolságra a rúd alsó végétől, körpályájának sugara

r = L cos 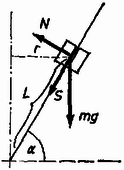α

(2. ábra).

2. ábra

Ha a test a felfelé csúszás határán van, a mozgásegyenletek:

\begin{matrix} m r ω^{2} = N sin α + S cos α, \\ 0 = m g - N cos α - S sin α . \end{matrix}

S

súrlódási erőt és az

N

nyomóerőt az

\begin{matrix} S \leq μ N \end{matrix}

feltételbe helyettesítve kapjuk, hogy

\begin{matrix} tg (α + ε) \geq ω^{2} r / g, ha α + ε < π / 2, \end{matrix}

ahol az

ε

súrlódási határszöget a

μ = tg ε

egyenlet adja meg. (Ha

α + ε \geq π / 2

test már csak lefelé mozdulhat el.)
Hasonlóan tárgyalható a lefelé csúszás esete. A súrlódási erő előjele a mozgásegyenletekben megváltozik, így az egyenlőtlenség [mivel

cos (α - ε) > 0

] a

\begin{matrix} tg (α - ε) \leq ω^{2} r / g \end{matrix}

alakot ölti.
Összefoglalva, a test helyben maradásának feltétele:

\begin{matrix} tg (α + ε) \geq \frac{ω^{2} L cos α}{g} \geq tg (α - ε), ha α + ε < π / 2, \\ (ω^{2} L cos α) / g \geq tg (α - ε), ha α + ε \geq π / 2. \end{matrix}

Elég bonyodalmas a négy változó szerepének a taglalása. Triviális, hogy nyugalomban levő rúd esetében, amikor

ω = 0

, az állandó helyzet feltétele:

ε \geq α

. Ha nincs súrlódás,

ε = 0

, csak ez a feltétel jelent egyensúlyt:

\begin{matrix} \frac{ω^{2} L cos α}{g} = tg α . \end{matrix}

Egyébként a rúdon egy

L_{a}

-tól

L_{j}

-ig terjedő intervallumon belül marad meg a test változatlan helyen. Ha

α \leq ε

, akkor az alsó határ a tengelyben van. A 3. ábra adott,

α = 30^{\circ}

-os rúdhelyzetnél mutatja meg az

m

tömegű test

L

távolságának nagyságát, mint

ω

függvényét.

ε = 0

-nál a szaggatott vonal mutatja a lehetséges egyensúlyi helyzeteket.

3. ábra

A súrlódás növekedésével mindig szélesebb sáv lép ennek helyébe, ábránkon

μ = 0, 268

ε = 15^{\circ}

esete látható.
A 4. ábra egy

ω = 10 s^{- 1}

szögsebességgel forgatott rudat mutat különböző helyzetekben; a súrlódási határszög ismét

ε = 15^{\circ}

. A rúd vastagon kihúzott részei jelzik azokat a helyeket, ahol a test a helyén marad.

4. ábra

L_{a}

alsó határ

α = 15^{\circ}

-ig alul a tengelyben marad, aztán mindig jobban felfelé húzódik, a végtelenig. Az

L_{j}

felső határ

α = 0^{\circ}

esetében

μ g / ω^{2}

, azután mindig feljebb húzódik.

60^{\circ}

-nál

0, 731

67, 5^{\circ}

-nál

1, 944

(ezek a helyek nem fértek rá a rajzra).

α = 90^{\circ} - ε = 75^{\circ}

fölött a felső határ végtelen, a tömeg minden

L_{a}

-nál nagyobb távolságban a helyén marad. A középső, pontozott görbe a súrlódás nélküli esetben érvényes egyensúlyi helyzeteket jelöli meg.
A stabilitás kérdését illetően az a helyzet, hogy kilépve a nyugalmat jelentő sávból a test vagy felrepül a rúd végére, vagy leesik az aljára. A súrlódás nélküli esetben az egyensúlyi helyzet labilis. Függőleges rúd esetében súrlódás mellett is az egész rúdon labilis az egyensúlyi helyzet és a test leesik az origóba.

2. feladat. Mi a feltétele annak, hogy egy vastag lencse gyújtótávolsága két különböző hullámhosszúságú fény esetében ugyanannyi legyen? Taglaljunk megvalósítható eseteket, figyelembe véve különböző alakú lencséket!

Megoldás. Először idézzük fel a vastag lencsék tulajdonságait (1. például a K. M. L. 1967. évi 8‐9. számának 163. oldalán). A lencse adatai: a gömbfelületek rádiusza

r_{1}

és

r_{2}

(homorú felszín esetében negatív), a vastagság

d

, a törésmutató

n

(5. ábr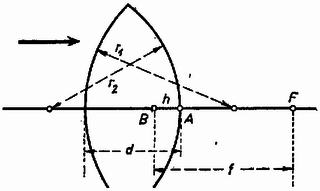a).

5. ábra

A fókusztávolság

f = B F

, amelyre

\begin{matrix} \frac{1}{f} = (n - 1) [\frac{1}{r_{1}} + \frac{1}{r_{2}} - d \cdot \frac{n - 1}{n} \cdot \frac{1}{r_{1} r_{2}}] . \end{matrix}

(1)

B

főpont távolsága a felszíntől:

\begin{matrix} B A = h = \frac{d r_{2}}{n (r_{1} + r_{2}) - d (n - 1)} . \end{matrix}

(2)

A lencse anyagának diszperziója van, ez azt jelenti, hogy különböző hullámhosszaknál más a törésmutató,

λ_{a}

-nál

n_{a}

λ_{b}

-nél

n_{b}

.
Az

(1)

összefüggést

n

hatványai szerint rendezve:

\begin{matrix} f (r_{1} + r_{2} - d) n^{2} + [2 f d - f (r_{1} + r_{2}) - r_{1} r_{2}] n - f d = 0. \end{matrix}

Az egyenlet

n

-ben másodfokú, tehát általában megvan annak a lehetősége, hogy adott

f

-hez két

n

tartozhassék és a feladatot megoldjuk.

(1)

-ből kifejezve a gyújtótávolságot:

\begin{matrix} f = \frac{n r_{1} r_{2}}{(n - 1) [n (r_{1} + r_{2}) - d (n - 1)]} . \end{matrix}

(3)

A feladat kérdésére úgy válaszolunk, hogy ezt a fókusztávolságot

n_{a}

és

n_{b}

törésmutatókra számítjuk ki és ezeket egyenlővé tesszük:

\begin{matrix} \frac{n_{a} r_{1} r_{2}}{(n_{a} - 1) [n_{a} (r_{1} + r_{2}) - d (n_{a} - 1)]} = \frac{n_{b} r_{1} r_{2}}{(n_{b} - 1) [n_{b} (r_{1} + r_{2}) - d (n_{b} - 1)]} . \end{matrix}

Az egyenlet rendezése ezt az egyszerű feltételt adja:

\begin{matrix} r_{1} + r_{2} = d (1 - \frac{1}{n_{a} n_{b}}) . \end{matrix}

(4)

A taglalás első lépéseként látjuk, hogy plankonvex vagy plankonkáv lencse esetében a feltétel nem teljesülhet, mert a baloldal végtelen volna, a jobb oldal pedig mindenképpen véges. Mivel a törésmutatók

1

-nél nagyobbak, a zárójeles rész

1

-nél kisebb lesz, tehát a rádiuszok összege kisebb lesz a vastagságnál, így általában igen vastag lencséket kapunk. Érdekes, hogy az

n_{a} - n_{b}

diszperzió nem szerepel a feltételben, csak a törésmutatók szorzata.
Áttekintés és taglalás céljából mérjük fel a koordinátatengelyekre

r_{1}

és

r_{2}

rádiuszokat

d

-ben mint egységben mérve (6. ábra).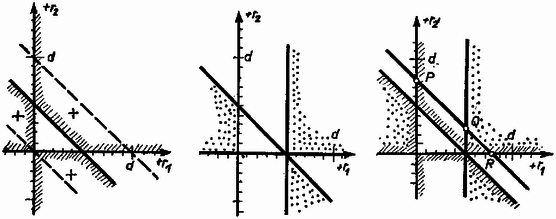

6. ábra

Először általánosságban, egyetlen törésmutató esetében vizsgáljuk a problémákat és példaként

n = 2

értéket tételezzünk fel, ami speciális flintüvegnél lehetséges. Megvizsgáljuk, mi a feltétele annak, hogy egy vastag lencse gyűjtőlencse legyen. Planparalel lemezként viselkedő lencsét akkor kapunk, ha

f = \infty

, vagyis

(3)

képletünk nevezője nulla:

\begin{matrix} (n - 1) [n (r_{1} + r_{2}) - d (n - 1)] = 0. \end{matrix}

Innen a feltétel:

\begin{matrix} r_{1} + r_{2} = d (1 - 1 / n) . \end{matrix}

A 6. ábra első rajzán

n = 2

esetében a vastag vonal tünteti fel az összetartozó értékpárokat, a ferde vonalat

r_{1} = 0, 5 d

és

r_{2} = 0, 5 d

között húzva (

n = 1

-nél az origón,

n = \infty

-nél a

(d, d)

pontokon mennének át ezek a ferde egyenesek). Gyűjtőlencsét akkor kapunk, ha

f > 0

, illetve

1 / f > 0

. A

(3)

összefüggés alapján:

\begin{matrix} \frac{(n - 1) [n (r_{1} + r_{2}) - d (n - 1)]}{n r_{1} r_{2}} > 0. \end{matrix}

Átrendezve:

\begin{matrix} \frac{r_{1} + r_{2}}{r_{1} r_{2}} > \frac{d}{r_{1} r_{2}} (1 - \frac{1}{n}) . \end{matrix}

Az első koordinátanegyedben akkor kapunk gyűjtőlencsét, ha

r_{1}

és

r_{2}

adatait a 6. ábra első rajzán látható vastag ferde vonal fölötti területről választjuk ki. Ha alatta választjuk ki, a vastag lencse két domború felülete ellenére szórólencse lesz. A többi koordinátanegyedben az előjelek tekintetében óvatosnak kell lennünk. A harmadik negyedben, ahol

r_{1}

és

r_{2}

negatív, a feltétel nem teljesülhet. A II. és IV. negyedben az egyenlőtlenség egy negatív tényezővel szorozva így alakul:

\begin{matrix} r_{1} + r_{2} < d (1 - \frac{1}{n}), \end{matrix}

tehát itt a vastag vonal alatti területek jelentik a gyűjtőlencsét. Ábránkon a vonalkázás jelzi a gyűjtőlencsék tartományát.
Lencsénk használatakor praktikus kívánság, hogy a fókusz az üveganyagon kívülre essék. Ennek feltétele

(2)

és

(3)

alapján:

\begin{matrix} \frac{n r_{1} r_{2}}{(n - 1) [n (r_{1} + r_{2}) - d (n - 1)]} > \frac{d r_{2}}{n (r_{1} + r_{2}) - d (n - 1)} . \end{matrix}

(5)

A fókusz akkor esik a kilépő felületre, ha

h = f

, amiből könnyen adódik az

r_{1} = d (1 - 1 / n)

feltétel. A 6. ábra második rajzán a

0, 5 d

-nél húzott függőleges jelenti ezt. Az első koordinátanegyedben, ahol minden rádiusz pozitív, a fókusz az anyagon kívülre esik, ha

r_{1} > d (1 - 1 / n)

, vagyis az

r_{1} r_{2}

pontnak a függőlegestől jobbra kell feküdnie. A többi koordinátanegyedben ismét óvatosnak kell lennünk. A III. negyedben a feltétel nem teljesülhet, mert

(5)

bal oldala itt negatív, jobb oldala pozitív. A II. negyedben egyszerűsíthetünk

r_{2}

-vel és az

(5)

alatti egyenlőtlenség csak úgy teljesülhet, ha a nevező a negatív:

\begin{matrix} n (r_{1} + r_{2}) - d (n - 1) < 0, \end{matrix}

amiből következik az itt érvényes feltétel:

\begin{matrix} r_{1} + r_{2} < d (1 - 1 / n) . \end{matrix}

A IV. negyed körülményeinek kivizsgálására írjuk fel

f

és

h

különbségét

(3)

és

(2)

felhasználásával:

\begin{matrix} \frac{n r_{1} r_{2} - d r_{2} (n - 1)}{(n - 1) [n (r_{1} + r_{2}) - d (n - 1)]} = r_{2} \cdot \frac{r_{1} - d (1 - 1 / n)}{(1 - 1 / n) [n (r_{1} + r_{2}) - d (n - 1)]} . \end{matrix}

Minthogy

r_{2}

negatív, ez a különbség csak úgy lehet pozitív, ha a nevező negatív, amiből következik:

\begin{matrix} r_{1} + r_{2} < d (1 - 1 / n) . \end{matrix}

Egyéb esetek kirekeszthetők. A 6. ábra középső rajzán pontozás jelöli meg azokat a területeket, ahol a használható

r_{1}

r_{2}

pontok feküsznek.
Ezután térjünk vissza eredeti problémánkra és rajzoljuk be ábránkba azon

r_{1}

r_{2}

pontok mértani helyét, amelyekre

n_{a}

és

n_{b}

törésmutatók esetében egyezők a fókusztávolságok (6. ábra harmadik rajza). A

(4)

feltétel egy egyenest jelent, amely a tengelyeket

d (1 - 1 / n_{a} n_{b})

távolságokban metszi. (Legyen példánkban

n_{a} = 2, 02

és

n_{b} = 1, 98

, ekkor

1 - 1 / n_{a} n_{b} = 0, 75

.) Ezen az egyenesen

P

-től balra olyan konvex-konkáv (!) szórólencséket találunk, amelyek fókusza az üvegben van.

P

-től

Q

-ig olyan bikonvex gyűjtőlencsék következnek, amelyek fókusza még mindig az anyagban van.

Q

-tól

R

-ig a fókusz az anyagon kívül van, ezek bikonvex gyűjtőlencsék.

R

-től lefelé konvex-konkáv szórólencséket találunk, de fókuszuk az üvegben van. Valamelyest praktikus értelmük csak a

Q R

közötti gyűjtőlencséknek van. Gyakorlatban ezek sem érnének sokat, mert hiába egyeznek a fókusztávolságok, ezeket a

B

főponttól kell felmérni, ennek helye pedig

(3)

szerint függ a törésmutatótól.

3. feladat.

P

pontból egyenlő tömegű, egyenlő

v

sebességű ionok indulnak el különböző irányokban. Ezeket egy

P R = 2 a

távolságban levő

R

pontban kell összegyűjteni adott

B

indukciójú homogén mágneses térrel, amely merőleges a rajz síkjára. A pályák legyenek a középvonalra szimmetrikusak

(7. ábra)

. Milyen legyen a mágneses tér határvonala?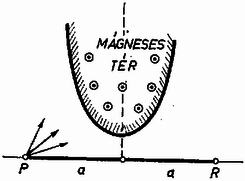

7. ábra

Megoldás. Homogén mágneses térben egy töltött rész körpályán mozog, közben a

Q

töltésre ható

Q v B

Lorentz-erő szolgáltatja az

m v^{2} / r

centripetális erőt:

Q v B = m v^{2} / r

, innen a körpálya sugara:

\begin{matrix} r = v m / Q B . \end{matrix}

A mi esetünkben a mágneses térben mindegyik ion ugyanakkora rádiuszú körpályán mozog. Pozitív ionok esetében hátulról előre irányuló mágneses térre van szükség. Amíg az ion a mágneses térben mozog, addig pályája az adott sugarú kör. Amint az ion kilép a térből, a kör utolsó pontjának érintője mentén repül tovább. A határvonalat úgy kell megválasztani, hogy valamennyi ion ugyanabba az

R

pontba repüljön. Ezt a matematikai problémát kell megoldani: hol kell a köröket abbahagyni, hogy az utolsó érintő eltalálja az

R

pontot. A szimmetria folytán elég az ábra egyik felével foglalkozni, továbbá a körök középpontjai az

y

-tengelyen vannak.
Az

r

sugarú körpályán repülő ion az

x

y

koordinátájú

A

pontban lép ki a térből és az érintő mentén repül

R

-be (8. ábr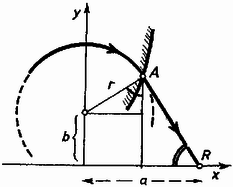a).

8. ábra

Hasonló háromszögekből: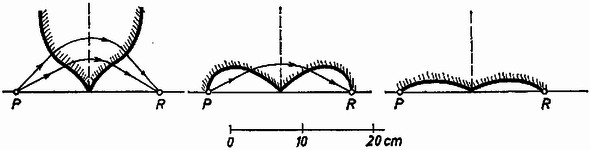

\begin{matrix} \frac{y - b}{x} = \frac{a - x}{y} . \end{matrix}

Azonkívül érvényes a kör egyenlete :

\begin{matrix} x^{2} + {(y - b)}^{2} = r^{2} . \end{matrix}

y

, illetve

(y - b)

kiküszöbölésével azonnal megkapjuk az ilyen tulajdonságú

A

-pontok mértani helyét, vagyis a mágneses tér határát megadó függvényt:

\begin{matrix} y = \frac{x (a - x)}{\sqrt[]{r^{2} - x^{2}}} . \end{matrix}

Ez negyedfokú függvény. A függvénygörbének csak az első koordinátanegyedbe eső részére van szükségünk és ezt tükrözzük az

y

tengelyre. A térhatárolás három esetét mutatja a 9. ábra.

9. ábra

A határvonalak típusa aszerint alakul, hogy az

a

távolság és az

r

pályasugár hogyan viszonylanak egymáshoz. Ábránkon

a = 10 cm

és a rádiuszok rendre

7, 5 cm

10 cm

és

20 cm

. Ha

1, 67 \cdot 10^{- 27} kg

tömegű,

1, 6 \cdot 10^{- 19}

coulomb töltésű oxigénionokról és

B = 0, 1

tesla erősségű térről van szó, akkor a szükséges

420 km/s

960 km/s

és

1920 km/s

repülési sebességek

2700

volt,

4800

volt és

19 200

volt gyorsító feszültségek hatására jönnek létre. Elvben mindegyik megrajzolt esetben a negyed-síkban kiinduló valamennyi ion összegyűjthető, de

r < a

esetében ehhez a végtelenig terjedő térre volna szükség. A határoló görbe végtelenbe menő ága akkor csap le hirtelen az

R

pontba, amikor

r

egyenlő lesz

a

-val. Még tovább növekedő

r

-nél a tér határvonala lelaposodik.

Kísérleti feladat. Egy két kivezetéssel bíró félvezető karakterisztikáját kellett felvenni azzal a kikötéssel, hogy a félvezető csak

0, 25

wattig terhelhető. Rendelkezésre álltak fix és változtatható ellenállások, két mérőműszer, valamennyi mérési területen megadott belső ellenállással és egy

9

voltos feszültségforrás. A mérés olyan természetű volt, hogy figyelembe kellett venni az ampermérőn létrejövő feszültségesést, illetve a voltmérő áramát. A karakterisztika elárulta, hogy a félvezető egy Zener-dióda volt.