| Cím: | 1975. évi fizika OKTV feladatai | ||
| Füzet: | 1975/október, 81 - 88. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | OKTV | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az általános és a szakosított tantervű osztályok versenyét külön rendezték meg. A feladatok részben ugyanazok voltak. Az I. forduló feladatai 1. feladat az általános tantervű osztályok részére. Hanglemezjátszó korongjára a középponttól -re pénzdarabot helyezünk. A súrlódási együttható a korong és a pénzdarab között . A korong nyugalmi helyzetéből indul. Szöggyorsulása állandó: . Mennyi idő múlva csúszik meg a pénzdarab a korongon? (Holics László) Megoldás. A korong szögsebessége . A pénzdarabra ható erő merőleges összetevője , sugárirányú összetevője (1. ábra). 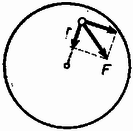 1. ábra A teljes erő: 2. feladat az általános tantervű és 1. feladat a szakosított tantervű osztályok részére. Az sugarú, tömegű tömör hengerhez elhanyagolható tömegű rúddal tömegű test van hozzáerősítve (2. ábra). Ez a henger tengelyétől távolságban van. A szerkezet labilis egyensúlyi helyzetéből kibillen. Mekkora sebességgel ütközik a tömeg a földhöz? A henger csúszás nélkül gördül. . 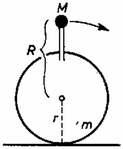 2. ábra (Vermes Miklós) Megoldás. Az tömegű test leesésével kapható munkavégzés (3. ábra) . 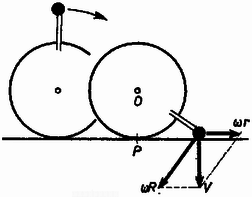 3. ábra Ez alakul át a henger, valamint az tömegű test haladó és forgó mozgásának mozgási energiájává. Könnyen belátható, hogy az tömegű test függőleges sebességgel ütközik a földhöz, mert a pillanatnyi forgási középpont . Legyen ekkor a henger szögsebessége . Az tömegű test sebességgel ütközik a földhöz, ez az pont haladási sebességének és az pont körüli forgás sebességének a vektoreredője: . Az energiatétel szerint: 2. feladat a szakosított tantervű osztályok részére. Az -es hajlásszögű lejtőn szán csúszik le. A rajta ülők higanyos barométerrel mérik a légnyomást. Ha a barométer csövét a lejtőre merőlegesen tartják, a higanyoszlop hossza , ha függőlegesen tartják, a higanyoszlop hossza . Mennyi a súrlódási együttható és mennyi a légnyomás? (Holics László) Megoldás. Először meg kell állapítanunk, hogy milyen irányú és nagyságú nehézségi gyorsulás észlelhető a szánon (4. ábra). 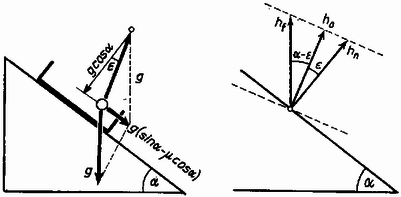 4. ábra Vizsgáljunk egy szánon lógó függőónt (K.M.L. 1973. 7. szám 82. oldal, illetve Dér ‐ Radnai ‐ Soós: Fizikai feladatok I., 23. o., 240. feladat). Az tömegű ingatestre ható súlyerőnek és a fonálban ható feszítőerőnek eredőként kell kiadnia a tömeget a lejtő mentén gyorsító nagyságú erőt. Ebből következik, hogy a függőón fonala a függőlegeshez képest szöggel hajlik vissza, ahol a súrlódási határszög: . A fonalat feszítő erő , ami kisebb, mint . A szánon a függőónra merőlegesen helyezkedik el a higany felszíne és a higany úgy viselkedik, mintha fajsúlya helyett kisebb volna, éspedig . Jelöljük a külső légnyomásnak nyugvó rendszerben megfelelő higanyoszlop magasságát -lal. A fonálinga irányában tartott Torricelli-csőben a higany magasságig emelkedne a higany kisebb hatásos fajsúlya következtében. Ha megdöntjük a csövet, a higanyoszlop vége a -ra rajzolt merőleges, a szaggatott vonal mentén marad. A derékszögű háromszögből , illetve értékét felhasználva: . Ebből a valóságos légnyomásnak nyugvó rendszerben megfelelő higanyoszlop magassága: . -re szintén derékszögű háromszögből kapunk összefüggést: 3. feladat az általános tantervű osztályok részére. Higannyal telt nagy edényben dugattyús henger lebeg (5. ábra). A dugattyúi fonál köti az edény aljához. A hengerben magasságban levegő van. A henger zárt vége -re van a higanyfelszín alatt. Milyen helyzetet foglal el a henger, ha a fonalat -rel megrövidítjük? (Vermes Miklós) 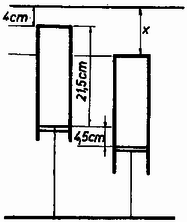 5. ábra Megoldás. Akkor van egyensúly, ha a henger fenekén a belső és külső nyomás egyenlő. Higany-cm-ben számolva alkalmazzuk a Boyle ‐ Mariotte törvényt: 3. feladat a szakosított tantervű osztályok részére. Higannyal telt alapterületű edényben alapterületű dugattyús henger lebeg. A dugattyút fonál köti az edény aljához. A hengerben magasságban levegő van. A henger zárt vége -re van a higanyfelszín alatt (6. ábra). a) Milyen helyzetet foglal el a henger, ha a fonalat -rel megrövidítjük? b) Ezután mekkora térfogatú higanyt kell az edénybe önteni, hogy a higany újra a régi magasságban álljon? (Vermes Miklós) 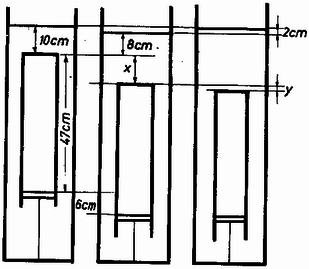 6. ábra Megoldás. a) A henger mozgásakor változik az edényben a higanyfelszín. Az edény és henger alapterületének az, aránya 1:2. Akkor van egyensúly, ha a henger fenekén egyeznek a nyomások. Ha a henger feneke -szel mozdul el lefelé, akkor az edényben a higanyfelszín -vel süllyed. A Boyle ‐ Mariotte törvény szerint: b) Alkalmazzuk a Bayle ‐ Mariotte törvényt az első és harmadik állapotra: A II. forduló feladatai: A feladatok mindkét csoportban ugyanazok voltak. 1. Az hosszú, tömegű deszka egyik végén csapágyazva függőleges helyzetben lóg. Egy tömegű lövedéket belelövünk a deszka alsó végébe úgy, hogy a lövedék bennragad a fában és a deszka fellendül. Mekkora sebességgel kell a lövedéket belelőni, rogy a deszka a vízszintes helyzetig emelkedjék fel (7. ábra)? (Vermes Miklós) 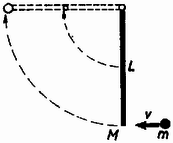 7. ábra Megoldás. Az úgynevezett ballisztikus ingáról van szó. A rugalmatlan ütközés alkalmával az impulzusmegmaradás törvényét kell alkalmaznunk. Mivel forgó mozgásról van szó, az impulzusnyomatékkal számolunk, amely egyetlen tömegpontnál az impulzus és rádiusz szorzata , merev testnél a szögsebesség és tehetetlenségi nyomaték szorzata . A belelövés pillanatában a deszka valamilyen szögsebességgel indul el, a lövedéket pedig úgy tekintjük, mintha sugarú körpályán érkezett volna. Ezért az impulzusnyomaték-megmaradás törvénye szerint: Elinduláskor a deszkának és a beleragadt lövedéknek együttes mozgási energiája: 2. Az sugarú, vízszintes helyzetű rúdra hosszú, hajlékony kötelet fektetünk (8. ábra). Kezdetben mindkét oldalon a kötél egyenlő hosszú darabja lóg le. A kötél bal oldali végét kissé lehúzva megszűnik a labilis egyensúlyi helyzet és a kötél bal oldalt teljesen lecsúszik. Milyen mélyen van a kötél alsó vége akkor, amikor ponttól kezdve elválik a rúdtól? A súrlódástól tekintsünk el. (Nagy László, Bodó Zalán, Párkányi László) 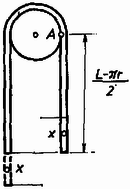 8. ábra Megoldás. Tekintsük változónak a kötél végének a kezdettől megtett útját. Eredetileg a kötél mindkét oldalon hosszan lóg le. Jelöljük -val az 1 méter hosszú kötél tömegét. Keressük a sebességet és a gyorsulást mint függvényét. Az energiamegmaradás törvénye szerint A gyorsulás: 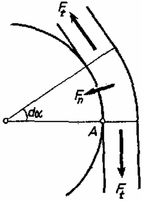 9. ábra A normálisan ható erőt a két érintőleges erőből kapjuk (10. ábra): 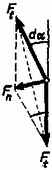 10. ábra 3. A 11. ábra szerinti kapcsolásban a két kondenzátor kapacitása egyenlő. A berendezésre os váltófeszültséget kapcsolva az áramerősség-mérő -t, a feszültségmérő ot jelez. Mennyit mutatnak a műszerek, ha a frekvenciát -ed részére csökkentjük? A feszültségmérőt végtelen ellenállásúnak, az áramerősség-mérőt elhanyagolható ellenállásúnak tekintsük. (Bodó Zalán) 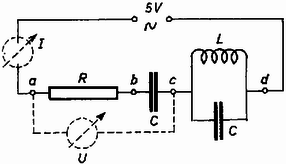 11. ábra Megoldás. Egy bizonyos pillanatban az áramerősség a megjelölt (a, b, c és d) pontok közötti szakaszokon ugyanaz. Az 5 volt az ezen pontok közötti feszültségek összege. Első feladatunk, hogy a kapcsolást az eredeti körfrekvencia mellett vizsgáljuk. Mivel mA és , az pontok közötti feszültség volt és így . Ez azt jelenti, hogy és között rezonancia van. Mivel kapacitív jellegű, a közötti párhuzamos rezgőkörnek induktív jellegűnek kell lennie: A és pontok közötti párhuzamos rezgőkör impedanciája: Az eredő impedancia és között: III. (kísérleti) forduló: A II. forduló dolgozatai alapján mindkét csoportból 11 ‐ 11 versenyző kísérleti fordulón vett részt Budapesten az ELTE Természettudományi Karának Általános Fizikai Tanszékén. Két feladattal foglalkoztak. Az egyikben egy vezetőnek a többfázisú mágneses térben való forgását tanulmányozták. A másikban egy homorú tükörben keletkező kép fényképfelvételét kellett elemezni. Az 1975. évi fizikai tanulmányi verseny eredménye: Éltalános tantervű osztályok: I, díj: Schmidt József (Esztergom, Dobó Katalin Gimn. IV. o. t., tanára: Sipos Imre). II. díj: Györgyi Géza (Budapest, Fazekas M. Gyak. Gimn. TV. o. t., tanára: Szalay Béla). III. díj: Sparing László (Szombathely, Nagy Lajos Gimn. IV. o. t., tanára: Rozmán Gyula és Hargitai Sándor) A további helyezettek: 4. Bérczi Tamás (Szeged, Ságvári E. Gyak. Gimn. IV. o. t., Kakuszi László), 5. Tarnóczy Tibor (Budapest, Apáczai Csere J. Gyak. Gimn. IV. o, t., Kelemen László), 6. Zsigmond Géza (Budapest, Fazekas M. Gyak. Gimn. III. o. t., Mihály István), 7. Vass Albert (Debrecen, Fazekas M. Gimn. TV. o. t., Deczky Béla), 8. Hettinger Ernő (Sopron, Széchenyi I. Gimn. TII. o. t., Légrádi Imre és Vass Béla), 9. Megyeri János (Budapest, József A. Gimn. IV. o. t., Ujj János), 10. Füle György (Aszód, Petőfi S. Gimn. ÍII. o. t., Barthus Zoltánné) Szakosított tantervű osztályok: I, díj: Szép Jenő (Budapest, Veres Pálné Gimn. IV. o. t., tanára: Kishonti Istvánné) II. díj: Somogyi József (Székesfehérvár, József A. Gimn. TV. o. t., tanára: Wolkensdorfer János) III. díj: Virosztek Attila (Szolnok, Verseghy F. Gimn. III. o. t., tanára: Sebestyén István) A további helyezettek: 4. Menyhárt Zoltán (Budapest, Eötvös J. Gimn. IV. o. t., Veres Mihályné), 5. Berger Ferenc (Baja, III. Béla Gimn. III. o, t., Pécsi József), 6. Faragó Béla (Csongrád, Batsányi J. Gimn. III. o. t., Szucsán András), 7. Szilágyi János (Debrecen, Kossuth L. Gimn. TV. o. t., Nagy Lászlóné), 8. Papp Zoltán (Mezőkövesd, I. László Gimn. TV. o. t., Varga András), 9. Horváth Ernő (Székesfehérvár, József A. Gimn. TV. o. t., Wolkensdorfer János), 10. Mészáros János (Szeged, Ságvári E, Gyak. Gimn. ÍV. o. t., Kocsis Vilmos) |