Cím: Sztatikailag határozatlan feladatok
Szerző(k):  Major János 
Füzet: 1975/szeptember, 34 - 36. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A sztatikai feladatok alaptípusában valamely nyugvó testre ható ismeretlen erőket kell meghatározni. Az ismeretlenek száma ebben az esetben megegyezik a függetlenül felírható sztatikai egyenletek számával. Mi a helyzet akkor, ha a sztatikai egyenletek számánál több ismeretlent tartalmaz a probléma? Ilyenkor a feladat sztatikailag már nem határozott, leggyakrabban az előzőleg merevnek tekintett test rugalmas tulajdonságait kell figyelembe vennünk.
A legegyszerűbb esetben a probléma egydimenziós: a testre ható erők egy egyenesbe esnek ‐ egyetlen egyenletet írhatunk fel az erők egyensúlyára. A feladat legyen pl. a következő:

 

Egy A keresztmetszetű gerendát, melynek hossza l, lineáris hőtágulási együtthatója α és a rugalmassági modulusa E, két erős fal közé falaznak. Milyen erők hatnak a gerendára, ha a hőmérséklet t-vel emelkedik? A súlyerőtől tekintsünk el, a két fal távolsága állandó (1. ábra).
 

 

1. ábra
 

A gerendára a két végén hat a falak nyomó ereje, F1, ill. F2. Az erők egyensúlyára felírt egyenlet: F1=F2. A sztatika tehát csak arra ad választ, hogy a két erő megegyezik, de hogy mennyi az F=F1=F2 érték, már nem. A hőtágulás és a rugalmasságtan törvényeit kell alkalmaznunk. A rúd, ha nem lenne beépítve, Δl=αlt-vel nyúlna meg a hőmérséklet növekedése miatt. Az F erő alkalmazásával éppen ezt a Δl nyúlást nyomjuk vissza. Hook törvénye szerint Δl=lF/AE. Ebből a két egyenletből már meghatározhatjuk az ismeretlen erőt:
F=αEAt
Konkrét adatokat behelyettesítve azt kapjuk, hagy az az erő igen nagy lehet ‐ a hidak konstrukciójánál éppen ezt a hatást kerülik el azzal, hogy csak az egyik oldalon építik össze szilárdan a hidat a parttal, a másik oldalon görgők, ill. " dilatációs hézag'' alkalmazásával szabadon mozoghat a híd vége a parthoz képest.
A gyakorlatban nem egydimenziós problémáknál a számolás általában sokkal komplikáltabb, legtöbbször gyakorlatilag nem kivitelezhető. Vizsgáljuk meg a következő példát:
 

Egy súlytalannak tekinthető rudat a 2. ábra szerint függőleges síkban a falhoz támasztunk. Milyen erők hatnak a rúdra, ha G súlyú terhet akasztunk a rúd közepére? A súrlódási együttható a rúd és a talaj, illetve a fal között egyaránt 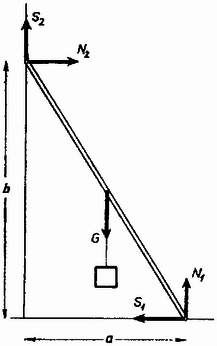μ.
 

 

2. ábra
 

A rúdra az ábrán berajzolt G, S1, S2, N1, N2 erők hatnak. Három sztatikai egyenletet írhatunk fel, feltételezve, hogy a rúd nyugalomban van:
0=N2-S1,0=S2-G+N1,0=N2b+G(a/2)-N1a.
Ez az egyenletrendszer adott G-re négy ismeretlent (N1, S1, N2, S2) tartalmaz, nem oldható meg egyértelműen. (Megváltozna a helyzet, ha pl. a falat simának tekintenénk, azaz az egyenletekhez még hozzávehetnénk az S2=0 egyenletet is.) Jelenleg azonban az egyenletrendszert nem tudjuk megoldani. Ennek szemléletesen az az oka, hogy az S1, és S2 súrlódási erők egyaránt a rúd lecsúszását gátolják, és az, hogy ezt a feladatot hogyan osztják el egymás között, nem sztatikai eredetű. S1 és S2 értéke attól függ, hogy hogyan helyeztük el a rudat és a súlyt. Például ha a rúdnak először az alsó végpontját tettük le a földre, akkor óvatosan úgy döntjük neki a falnak, hogy a felső végére közben nem túlságosan nagy felfelé irányuló erőt fejtünk ki, elengedés után S2 is felfelé fog hatni. Ha azonban a falhoz döntéskor a rudat kissé összenyomjuk, elérhető az S2<0 eset, azaz S2 a súlyerővel együtt a rudat lefelé mozdítaná, de S1 nagyobb értéke a rúd lecsúszását megakadályozza. Kellő módon odatámasztva a rudat, így megvalósítható az S2=0 eset is.
Látjuk, hogy S2 értéke attól függ, hogy a rudat milyen körülmények között támasztottuk a falnak, illetve a nekitámasztáskor a rúd összenyomott, vagy széthúzott állapotban volt-e. Ez az igen kis, szemmel nem észlelhető, de viszonylag nagy erőt eredményező mechanikai deformáció a meghatározó. S2 és így S1, N1 és N2 értéke is attól függ, hogy milyen rugalmas állapotban (megfeszítve, összenyomva, erőmentesen) van a rúd , azaz általában azt mondhatjuk, hogy S1 és S2 értéke a rúd rugalmas tulajdonságaitól és az odahelyezés módjától függ.
Természetesen mindig érvényesek az
S1≤μN1;S2≤μN2
egyenlőtlenségek.
Ha kérdésünk az lenne, hogy maximálisan mekkora G súlyt akaszthatunk a rúdra, hogy az meg ne csússzék, a feladat sztatikailag határozottá válnék. A súly növelésével a súrlódási erőkre és a nyomóerőkre felírt egyenlőtlenségek egyre jobban eltolódnak az egyenlőség felé, majd amikor az egyik egyenlőtlenség egyenlőségbe megy át (az egyenletek száma eggyel nő), a feladat már sztatikailag megoldható. Természetesen a rúd csak a súly további növelése után csúszik meg, amikor a másik egyenlőtlenség is egyenlőségbe megy át ‐ csúszáskor S1=μN1 és S2=μN2. Ezzel a két határesetet kifejező egyenlettel együtt a három sztatikai egyenlet olyan egyenletrendszert ad, amiből a súlyerő maximális értéke is kiszámítható.