Cím: Nagyon szimmetrikus kombinatorikai struktúrák
Szerző(k):  Pelikán József 
Füzet: 1975/október, 53 - 60. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Szokás azt mondani, hogy a kombinatorika a véges halmazok tudománya. Ez a meghatározás azonban nemcsak semmitmondó (mert belőle nem nagyon lehet elképzelni, hogy milyenek valójában a kombinatorika tételei és bizonyítási módszerei), hanem megtévesztő is mert azt a benyomást kelti a témakörben járatlan személyben, mintha a kombinatorika triviális kérdések tanulmányozásából állna ‐ ugyan mi érdekeset lehet egy véges halmazról mondani?). Ezzel szemben a kombinatorika nagyszámú mély tétellel, ugyanakkor számos régóta megoldatlan problémával rendelkező önálló diszciplína. Különösen vonzóvá teszi az, hogy még a legnehezebb megoldatlan problémák megértéséhez sem kell különösebb matematikai képzettség; az iskolai matematika tökéletesen elegendő.
Az alábbiakban a kombinatorikának csupán egy speciális területéről szeretnék néhány eredményt és problémát ismertetni; az itt vizsgált objektumokat talán leghelyesebb "nagyon szimmetrikus kombinatorikai struktúrák''-nak nevezni.

 

1. Véges projektív síkok
 

Könnyen látható, ha a közönséges (euklideszi) sík minden egyeneséhez hozzáveszünk egy új, ún. "végtelen távoli'' pontot, mégpedig két egyeneshez akkor és csak akkor vesszük hozzá ugyanazt a végtelen távoli pontot, ha a két egyenes párhuzamos, továbbá azt mondjuk, hogy a végtelen távoli pontok alkossanak egy egyenest (az ún. végtelen távoli egyenest), akkor ‐ most már nem téve különbséget a régi és az újonnan bevezetett pontok és egyenesek között ‐ igazak a következő állítások:
1. Bármely két ponton át egy és csak egyenes halad.
2. Bármely két egyenesnek egy és csak egy közös pontja van.
3. Van négy olyan pont, hogy közülük semelyik három sem fekszik egy egyenesen.
Ezt a kibővített síkot valós projektív síknak nevezzük. A projektív sík sok szempontból szabályosabb, mint a közönséges euklideszi sík; ez utóbbiban például a 2. állítás nem teljesül.
Eddig az 1., 2., 3. állításokat úgy tekintettük, mint bizonyos, a valós projektív síkra vonatkozó tételeket. Most nézzük ezeket más szemszögből: tekintsük ezeket a projektív sík axiómáinak! Mit jelent ez? Tegyük fel, hogy adott egy H halmaz (bizonyos dolgok összessége). A H halmaz elemeit pontoknak fogjuk nevezni. Tegyük fel továbbá, hogy ki vannak jelölve a H halmaz bizonyos részhalmazai; e részhalmazokat egyeneseknek fogjuk nevezni. Az így definiált pontokat és egyeneseket projektív síknak fogjuk nevezni, ha teljesülnek rájuk az 1., 2., 3. állítások.
Ezek után látjuk, hogy a fentebb megkonstruált valós projektív sík egy példa projektív síkra, de más példák is lehetségesek. Minkét a továbbiakban az olyan példák érdekelnek, ahol a H véges halmaz (tehát csak véges sok eleme van), az ilyen projektív síkokat véges projektív síknak fogjuk nevezni.
Léteznek-e ilyenek egyáltalán? Léteznek, mégpedig a legegyszerűbb az, ami az 1. ábrán látható.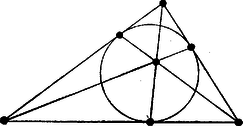
 

 

1. ábra
 

Ezt az ábrát a következőképpen akarjuk értelmezni: a H halmaz elemei (a "pontok'', írjuk ezekhez egy csúcsból kiindulva a kerület mentén egymás után az 1, 2, 3, 5, 7, 6 számokat, középre 4-et. Az "egyenesek'' pedig a H-nak olyan háromelemű részhalmazai, amelyek az ábrán egy egyenesre esnek (tehát pl. 123, 145 stb.), továbbá még egy "egyenes'' az, ami az ábrán körnek látszik (tehát 256). Az olvasó ellenőrizze, hogy mind a három axióma teljesül! Ugyanennek a véges projektív síknak egy más megadási módja szerepel a 2. ábrán: itt egyszerűen felsoroljuk egymás után H-nak azokat a részhalmazait, amelyeket egyeneseknek akarunk nevezni.
 

 

2. ábra
 

A 3. ábrán a következő legegyszerűbb véges projektív síkot adjuk meg a 2. ábráéhoz hasonló "táblázatos'' módszerrel.
 

 

3. ábra
 

Itt a H halmaz elemeit az 1-től 13-ig terjedő számok jelölik, egyeneseknek pedig H-nak azokat a négyelemű részhalmazait nevezzük, amelyek a 3. ábra valamelyik sorát alkotják.
Az eddig megismert véges projektív síkok tulajdonságait jobban szemügyre véve, arra a sejtésre juthatunk, hogy a következő tétel igaz:
 

1. tétel: Minden véges projektív síkhoz létezik egy olyan n természetes szám (n≥2), hogy az alábbi állítások mindegyike igaz:
1. Minden egyenesen n+1 pont van.
2. Minden ponton n+1 egyenes megy át.
3. Az összes pontok száma n2+n+1.
4. Az összes egyenesek száma n2+n+1.
Nem nehéz bebizonyítani, hogy ez a tétel valóban igaz. (Az olvasó önállóan is megpróbálkozhat vele.) A szóban forgó n-et az illető véges projektív sík rendjének nevezzük. A 2., ill. 3. ábrán szerelő véges projektív síkok rendje n=2, ill. n=3, tehát a két legkisebb lehetséges érték; ezért mondtuk, hogy ezek a legegyszerűbb véges projektív síkok.
Vegyük észre, hogy az 1. tételnek számos nem-triviális következménye van. Rögtön látjuk például, hogy ha egy N természetes szám nem n2+n+1 alakú (alkalmas n≥2 természetes számra), akkor egy N pontú halmazon biztosan nem lehet véges projektív síkot csinálni. Márpedig ez az állítás önmagában egyáltalán nem nyilvánvaló!
Felmerül a kérdés, hogy az 1. tétel mennyire megfordítható. Az 1. tétel ugyanis csak azt állítja, hogy minden véges projektív síkhoz létezik egy, az ott megfogalmazott tulajdonságokat kielégítő n szám. Azt viszont nem állítja, hogy ha megadunk egy n≥2 természetes számot, akkor biztosan kiválaszthatók az n2+n+1 elemű halmaznak olyan n+1 elemű részhalmazai, amelyek egy véges projektív síkot alkotnak. Tehát azt kellene tudnunk, hogy mely n≥2 természetes számokra létezik valóban n-edrendű véges projektív sík. ‐ Bebizonyítható, hogy ha n prímhatvány: n=pk (p prím, k≥1), akkor tényleg létezik n-edrendű véges projektív sík. (A bizonyítás nem nehéz, de bizonyos algebrai előismereteket igényel.) Megoldatlan viszont (s egyike a nagyon szimmetrikus kombinatorikai struktúrákra vonatkozó leghíresebb megoldatlan problémáknak) az alábbi
 

1. probléma: Igaz-e, hogy ha létezik n-edrendű véges projektív sík, akkor n prímhatvány?
Tudjuk-e egyáltalán valamilyen n-re, hogy nem létezik n-edrendű véges projektív sík? Ebben az irányban minden, amit tudunk, a következő tételben szerepel (a tételt R. H. Bruck és H. J. Ryser bizonyították 1949-ben egy nagyon szellemes algebrai-számelméleti gondolatmenet segítségével):
 

2. tétel (Bruck ‐ Ryser): Ha n≥2 olyan természetes szám, ami 4-gyel osztva 1-et, vagy kettőt ad maradékul és n nem állítható elő két négyzetszám összegeként, akkor nem létezik n-edrendű véges projektív sík.
(Az olvasó azt kérdezheti: hogyan lehet könnyen eldönteni egy számról, hogy előáll-e két négyzetszám összegeként? Válasz: n akkor és csak akkor nem áll elő két négyzetszám összegeként, ha van olyan 4k+3 alakú prímszám, ami n prímtényezős felbontásában páratlan kitevőn szerepel.)
A tétel mutatja például, hogy nem létezik n=6 rendű véges projektív sík. Tekintve, hogy n=2,3,4,5,7,8,9 prímhatványok, a következő kérdéses eset 10. Erre a Bruck ‐ Ryser-tétel nem alkalmazható, mert 10=32+12.
 

2. probléma: Létezik-e 10-edrendű véges projektív sík?
(Bizonyára van olyan olvasó, akiben felmerül a gondolat: miért nem próbálják ki ezt egy elektronikus számológépen? Amikor ilyen kicsi számról van szó, mint a 10, a számológép nyilván néhány perc vagy talán néhány másodperc alatt végigpróbálgatná az összes esetet. Azonban az a helyzet, hogy az itt szükséges próbálgatások száma olyan nagy, hogy még a ma ismert leggyorsabb számológépekkel is reménytelenül hosszú ideig tartana.)
Nézzünk most egy másik kérdést: Igaz-e, hogy rögzített n mellett az n-edrendű véges projektív síkok mind "ugyanolyanok''? "Ugyanolyanok'' alatt azt értjük, hogy csak a jelölésben különböznek, vagyis precízen fogalmazva: akkor mondjuk, hogy két n-edrendű véges projektív sík "ugyanolyan'', ha az egyik pontjaihoz kölcsönösen egyértelműen hozzá lehet rendelni a másik pontjait úgy, hogy az egyik projektív síkban bizonyos pontok pontosan akkor alkossanak egy egyenest, ha a másik projektív síkban nekik megfelelő pontok egy egyenest alkotnak. (A továbbiakban, alkalmazva a matematikában szokásos elnevezést, nem azt mondjuk, hogy a két véges projektív sík "ugyanolyan'', hanem hogy izomorf.)
Az olvasó különösebb nehézség nélkül bebizonyíthatja, hogy bármely két másodrendű véges projektív sík izomorf. Ugyancsak izomorf bármely két n-edrendű projektív sík n=3,4,5,7 és 8 esetén (bár a bizonyítás egyre nehezebb lesz). Viszont n=9-re a megfelelő állítás már nem igaz: létezik 4 lényegesen különböző (tehát páronként nem-izomorf) 9-edrendű véges projektív sík. Ismert az, hogy ha n=pk>8(pprím,k>1), akkor van két nem-izomorf n-edrendű véges projektív sík. Megoldatlan viszont az alábbi
 

3. probléma: Igaz-e, hogy bármely két p-edrendű (p prím) véges projektív sík izomorf?
Persze a véges projektív síkok létezésének és izomorfiájának kérdése csak kis része az itt vizsgált kérdéseknek. A legkiterjedtebben vizsgált (és legtermészetesebb) kérdés az, hogy milyenek a létező véges projektív síkok? Ízelítőül egy problémát ismertetek.
Az n-edrendű véges projektív sík pontjainak olyan részhalmazát szeretnénk kiválasztani, hogy minden egyenes tartalmazzon legalább egyet a kiválasztott pontok közül. Nevezzük az ilyen ponthalmazt lefogó pontrendszernek. Könnyű látni, hogy egy lefogó pontrendszer legalább n+1 pontot kell, hogy tartalmazzon. Ugyancsak könnyű látni, hogy n+1 elemű lefogó pontrendszer mindig található: a sík akármelyik egyenesének összes pontját választva, lefogó pontrendszert kapunk (ez a 2. axióma közvetlen következménye). Nyilván lefogó pontrendszer lesz akkor minden olyan ponthalmaz is, ami tartalmaz egy teljes egyenest. Nevezzünk tehát nem-triviális lefogó pontrendszernek egy olyan lefogó pontrendszert, ami nem tartalmaz teljes egyenest. Kérdés, hogy egy nem-triviális lefogó pontrendszernek legalább hány eleme van. 1969-ben bizonyítottam az alábbi tételt:
 

3. tétel: Az n-edrendű véges projektív síkban (n≥3) egy nem-triviális lefogó pontrendszer elemszáma több, mint
n+12n.
 

2. Ortogonális latin négyzetek
 

Tegyük fel, hogy egy n×n-es "sakktábla'' minden mezőjébe beírjuk az 1-től, n-ig terjedő természetes számok valamelyikét, mégpedig úgy, hogy minden sorban és minden oszlopban is az 1-től n-ig terjedő számok mindegyike pontosan egyszer szerepeljen. Egy ilyen alakzatot n×n-es latin négyzetnek nevezünk. Egy 4×4-es latin négyzetet látunk a 4. ábrán.
Tekintsünk most két n×n-es latin négyzetet. Vegyünk egy harmadik n×n-es sakktáblát és ennek minden mezőjére írjuk be azt a számpárt, aminek első tagja az a szám, ami az első latin négyzetben áll ezen a mezőn, második
1234MMMM1234MMMM(1,1)(2,2)(3,3)(4,4)2143MMMM4321MMMM(2,4)(1,3)(4,2)(3,1)4321MMMM3412MMMM(4,3)(3,4)(2,1)(1,2)3412MMMM2143MMMM(3,2)(4,1)(1,4)(2,3)4. ábraMMMMM5. ábraMMMMMMMM6. ábra
tagja pedig az a szám, ami a második latin négyzetben áll ezen a mezőn. Ha ily módon a lehetséges n2 számpár mindegyikét megkapjuk pontosan egyszer, akkor azt mondjuk, hogy a két n×n-es latin négyzet ortogonális egymásra. Az 5. ábrán egy olyan 4×4-es latin négyzet látható, ami ortogonális a 4. ábrán látható latin négyzetre; a 6. ábra mutatja, hogy tényleg ortogonálisak.
Ha nem kettő, hanem több n×n-es latin négyzetünk van, akkor mondjuk, hogy ezek páronként ortogonálisak, ha közülük bármely kettő ortogonális. Felmerül a kérdés, hogy legfeljebb hány n×n-es latin négyzetet lehet megadni úgy, hogy páronként ortogonálisak legyenek? A válasz az alábbi tétel, melyet az olvasó maga is könnyen bebizonyíthat:
 

4. tétel: Az n×n-es páronként ortogonális latin négyzetek száma legfeljebb n-1.
Ismét felmerül a kérdés, hogy n-1 páronként ortogonális n×n-es latin négyzet tényleg megadható-e? Már az sem triviális, hogy két ortogonális n×n-es latin négyzet megadható. Ha n 4-gyel osztva nem 2-t ad maradékul (és ≥3), akkor némi ügyeskedéssel belátható, hogy létezik két ortogonális n×n-es latin négyzet.
Leonhard Euler (1707‐1783), a XVIII. század nagy matematikusa azt sejtette 1782-ben, hogy ha n 4-gyel osztva 2-t ad maradékul, akkor nem létezik két ortogonális n×n-es latin négyzet. Ezt a sejtést már a legegyszerűbb esetben (n=6) sem sikerült bebizonyítani több, mint 100 évig. (Az n=6 eset a "36 tiszt problémája'' néven is ismeretes. A kérdés ugyanis Euler fogalmazásában eredetileg így hangzott: Van 6 különböző ezred mindegyikéből 6‐6 tiszt. Az egy ezredből való tisztek mind különböző rendfokozatúak, de a szóban forgó 6 rendfokozat mindegyik ezred esetében ugyanaz. Felállítható-e ez a 36 tiszt egy 6×6-os alakzatba úgy, hogy minden sorban és minden oszlopban az ott álló 6 tiszt csupa különböző ezredből való és csupa különböző rendfokozatba tartozik? Az olvasó bizonyítsa be, hogy ez a kérdés valóban ekvivalens két 6×6-os ortogonális latin négyzet létezésének kérdésével!) 1900-ban sikerült csak kimutatnia G. Tarry-nek, hogy valóban nem létezik két 6×6-os ortogonális latin négyzet.
A következő, n-10 eset csaknem 60 évig továbbra is megoldatlan maradt. Annál nagyobb volt a meglepetés, amikor E. T. Parker 1959-ben kimutatta, hogy létezik két ortogonális 10×10-es latin négyzet, majd R. C. Bose, S. S. Shrikhande és E. T. Parker 1960-ban kimutatták, hogy minden 10-nél nagyobb 4k+2 alakú n számra is létezik két n×n-es ortogonális latin négyzet. A nagy Euler tehát ezúttal tévedett! Parker híres konstrukcióját, a két ortogonális 10×10-es latin négyzetet a 7. ábrán mutatjuk be. (Az ábrán 10 helyett mindenütt 0-t írtunk.) ‐ Létezik-e három, páronként ortogonális 10×10-es latin négyzet? Senki nem tudja.
0417298365MMMMMM07869354128152739406MMMMMM61780945239826374510MMMMMM50278196345983047621MMMMMM96137820457698415032MMMMMM39024781566709852143MMMMMM84913572603071986254MMMMMM78592463011234560789MMMMMM45601237892345601897MMMMMM12345609784560123978MMMMMM2345601897M7. ábra

Az olvasó azt mondhatja: mindez érdekes, de tulajdonképpen öncélú játék, hiszen semmi más matematikai problémához nincsen semmi köze, vagyis nem "alkalmazható''. Feltehetőleg megváltozik azonban az olvasó véleménye, ha elolvassa a következő tételt:
 

5. tétel: Akkor és csak akkor létezik n-edrendű véges projektív sík, ha létezik n-1 darab, páronként ortogonális n×n-es latin négyzet.
Tehát az az állítás, hogy nem létezik 6-odrendű projektív sík, következménye Tarry idézett eredményének, és általában is a páronként ortogonális n×n-es latin négyzetek maximális számára vonatkozó kérdés finomítása az n-edrendű véges projektív sík létezésére vonatkozó kérdésnek. A következő probléma pedig a 2. probléma finomítása:
 

4. probléma: Mennyi a páronként ortogonális 10×10-es latin négyzetek maximális száma?
Mint a fentiekből tudjuk, jelenleg csak az ismeretes, hogy a válasz legalább 2 és legfeljebb 9.
 

3. Blokkrendszerek
 

Kísérletek tervezésénél gyakran merül fel az alábbi konkrét példához hasonló probléma:
Tegyük fel, hogy bizonyos gyógyszerek együttes hatását akarjuk vizsgálni. Összesen v fajta gyógyszerről van szó és minden kísérleti állatnak k fajtát adunk ezek közül. A kísérlet statisztikai kiértékelése akkor lenne a legkényelmesebb, ha akárhogyan választva ki a v fajta gyógyszer közül k-t (mint tudjuk, ez
(vk)=v(v-1)⋅...⋅(v-k+1)1⋅2⋅...⋅k
-féleképpen lehetséges), lenne egy olyan kísérleti állat, ami éppen ezt a k fajta gyógyszert kapja. Csakhogy (vk) általában igen nagy szám és könnyen lehet, hogy nem áll rendelkezésre ennyi kísérleti állat, vagy az ehhez szükséges gyógyszermennyiség. De ha rendelkezésre is állnának, ilyen nagy számú kombináció kipróbálása igen magas költségeket eredményezne.
Ezért általában arra kényszerülünk, hogy csak bizonyos k-as kombinációkat próbáljunk ki. Ha azonban azt akarjuk, hogy kísérletünkből két gyógyszer kölcsönhatására vonatkozólag statisztikailag értékelhető eredményeket kapjunk, úgy kell a k-as kombinációkat megválasztanunk, hogy akárhogyan választva a v gyógyszer közül kettőt, mindig ugyanannyi (mondjuk λ darab) kísérleti állat legyen, amelyik mind a két gyógyszert kapja, más szóval, hogy a kiválasztott k-asok között pontosan λ olyan legyen, amelyik ezen két gyógyszer mindegyikét tartalmazza.
Most már látjuk, milyen gyakorlati igény motiválja az alábbi definíciót.
Tegyük fel, hogy egy v elemű halmaznak kiválasztjuk bizonyos k elemű részhalmazait úgy, hogy a v elemű halmaz bármely két elemét pontosan λ darab kiválasztott részhalmaz tartalmazza. Ekkor nem nehéz belátni, hogy a v elem mindegyike ugyanannyi kiválasztott részhalmazban van benne. Ezt a számot r-rel jelöljük, a kiválasztott részhalmazok számát pedig jelöljük b-vel. A továbbiakban a kiválasztott részhalmazokat blokkoknak fogjuk nevezni. Egy ilyen struktúrát blokkrendszernek fogunk nevezni, vagy ha a paramétereket is fel akarjuk tüntetni, (v,b,r,k,λ)-blokkrendszernek. A triviális esetek kizárására a továbbiakban feltesszük, hogy a paraméterekre teljesülnek a 2≤k<v,λ≥1 egyenlőtlenségek.
Ez a fogalom a véges projektív sík fogalmának általánosítása, hiszen minden n-edrendű véges projektív sík egyben egy (v,b,r,k,λ)-blokkrendszer is, ahol

v=b=n2+n+1,r=k=n+1,λ=1.



A paraméterek között fennállnak a következő összefüggések:
 

6. tétel: Minden (v,b,r,k,λ)-blokkrendszerre teljesül:
bk=vr,r(k-1)=λ(v-1),b≥v.

Ezek közül az első kettőt az olvasó maga is könnyen bebizonyíthatja, a harmadiknak (ez az ún. Fisher-egyenlőtlenség) a bizonyítása viszont nehezebb.
A 6. tételből könnyen látható:
b=λv(v-1)k(k-1),
amely szám általában sokkal kisebb, mint (vk). Illusztrációképpen gondoljuk meg, hogy ha a fent említett kísérletnél mondjuk egy 11-edrendű projektív sík egyeneseinek megfelelően választjuk a gyógyszereket (v=b=133,k=12,λ=1), akkor 133 kísérleti állatra van szükség. Ugyanakkor (13312)≈3,8⋅1016; bizonyosan állíthatjuk, hogy a Földön nem él ennyi tengerimalac.
A 6. tételben szereplő feltételek ismét csak szükséges, de nem elégséges feltételek (v,b,r,k,λ)-blokkrendszer létezésére. Pl. v=b=43,r=k=7,λ=1 esetén a 6. tételben szereplő összefüggések teljesülnek, még sincs (43,43,7,7,1)-blokkrendszer. (Ez a 2. tételből következik, ugyanis egy ilyen blokkrendszerről nem nehéz belátni, hogy az egy 6-odrendű véges projektív sík lenne, lásd 7. tétel.) Blokkrendszerek létezésének kérdését nagyon sokat vizsgálták, de továbbra is igen sok az eldöntetlen kérdés. Nem ismeretes pl. (hogy egy viszonylag kis paraméterekből álló példát említsünk), hogy létezik-e (v,b,r,kλ)=(22,23,12,8,4) paraméterekkel blokkrendszer.
Egy blokkrendszerben két blokk közös elemeinek száma általában nem ugyanaz bármely két blokkra. Viszont igaz az alábbi
 

7. tétel: Ha egy (v,b,r,k,λ)-blokkrendszerben v=b (ekkor szükségképpen r=k is teljesül), akkor bármely két blokknak λ közös eleme van.
Ugyanilyen blokkrendszerekről szól a
 

8. tétel: Ha egy (v,b,r,k,λ)-blokkrendszerben v=b páros szám, akkor k-λ teljes négyzet.
Ez a tétel mutatja, hogy pl. (v,b,r,k,λ)=(22,22,7,7,2) paraméterekkel nem létezik blokkrendszer, pedig a paraméterek kielégítik a 6. tételben szereplő feltételeket.
A blokkrendszerekéhez hasonló a t-blokkrendszer definíciója (t≥2): egy v elemű halmaz bizonyos k elemű részhalmazai (ezeket hívjuk blokkoknak) t-blokkrendszert alkotnak, ha a v elemű halmaz minden t elemű részhalmazát pontosan λ darab blokk tartalmazza. (A blokkrendszerek ebből a t=2 speciális esetben adódnak.) Nem nehéz belátni, hogy minden t-blokkrendszer egyben t'-blokkrendszer is minden t'<t(t'≥2) értékre (persze t'-blokkrendszerként tekintve, más lesz a λ értéke). Speciálisan minden t-blokkrendszer egyszersmind blokkrendszer is. Triviálisnak nevezzük az olyan t-blokkrendszert, amit úgy kapunk, hogy blokkoknak választjuk a v elemű halmaz összes k elemű részhalmazait (t≤k≤v). Mindössze két nem-triviális 5-blokkrendszer ismeretes (az egyiknél v=24,k=8, a másiknál v=12,k=6) és megoldatlan az alábbi
 

5. probléma: Létezik-e nem-triviális 6-blokkrendszer?
 

A fentiekben a nagyon szimmetrikus kombinatorikai struktúrákra vonatkozó kérdéseknek csak egy egészen kis töredékét érintettük. Még csak említésre sem kerültek pl. a hibajavító kódok, amelyek az információelméletben, valamint a hírközlés elméletében (és gyakorlatában) rendkívül fontosak.
Végül megemlítjük, hogy mindazoknak a tételeknek a bizonyítása, amelyekről külön nem jeleztük, hogy az olvasó is könnyen bebizonyíthatja őket, kivétel nélkül a középiskolai anyagon túlmenő algebrai módszerekkel történik, ami szintén jelzi, hogy a kombinatorikai problémák szorosan kapcsolódnak a matematika más ágaihoz.
 

4. További irodalom
 

Blokkrendszerekre és latin négyzetekre vonatkozólag további információkat találhat az olvasó az alábbi szakköri füzetben:
Lovász László ‐ Pelikán József ‐ Vesztergombi Katalin: Kombinatorika (az általános és a középiskolai matematikai szakkörök számára). Tankönyvkiadó, Bp. 1970. II. kiadás, 1972. (Blokkrendszerekről a 4. fejezet szól, a további fejezetek egyéb ‐ nemszimmetrikus kombinatorikai struktúrákat, pl. gráfokat tárgyalnak. Ugyanott számos feladat is található.)
Jó áttekintést ad és számos itt nem vizsgák kérdést tárgyal az alábbi ismertető cikk:
Rényi Alfréd: Véges geometriák kombinatorikai alkalmazásai I. Matematikai Lapok 17 (1966) 33‐76. ‐ (Szerepel benne az előző pont végén említett algebrai módszerek alapjainak ismertetése is.)
A témakör legrészletesebb tárgyalása magyar nyelven az alábbi könyvben található: Kárteszi Ferenc: Bevezetés a véges geometriákba. Akadémiai Kiadó, Bp. 1972.