Kezdőlap


Cím:	A csonthéjas ikergyümölcs mértani alakzatáról
Szerző(k):	Szőke Béla
Füzet:	1975/március, 101 - 107. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A természet jelenségeinek és képződményeinek törvényszerűségeit vizsgálva sokszor úgy látszik, mintha a természet világa olyan kísérleti műhely volna, amely a lehetséges megoldások közül kikutatja és megvalósítja a legcélszerűbbet. Gondoljunk néhány közismert esetre: Ha $A$ egyénnek a $t$ tópartról egy kancsó vizet kell vinnie $B$ -hez, akkor $A$ bizonyára ,,érzék szerint'' az 1. ábrán látható ferde irányban (és nem merőlegesen) indul a part felé.

1. ábra

Felrajzolva az

A

ponthoz

t

egyenesre szimmetrikus

A'

pontot, majd megvonva

A' B

egyenest, mely

t

-szimmetriatengelyt

T

pontban metszi, látjuk, hogy

A' T = A T

, és így

\begin{matrix} A' T + T B = A T + T B = A' B \end{matrix}

szakasz hosszával. A

T

pont ilyen választásakor

A

tehát valóban a legrövidebb úton éri el

B

-t.
Ismeretes, hogy a fény

t

tükörfelületről ugyanilyen úton jut

A

-ból

B

-be. Nyilvánvaló, hogy ebben az esetben adott sebesség mellett a legrövidebb út egyszersmind a legrövidebb időt is jelenti.
Lássuk most, milyen úton jut el a legrövidebb idő alatt

A

a tó túlsó partján levő

B

-hez, ha futási sebessége

c_{1}

és úszási sebessége

c_{2}

? Nyilván arra fog törekedni, hogy a futási sebességét használja ki jobban, mivel

c_{1} > c_{2}

.
Ha egyenes irányban akarná elérni

B

-t, akkor csak

A T_{1}

úton futhatna és

T_{1} B

hosszú távon már úsznia kellene. Bizonyára a tópartnak olyan

T

pontjáról igyekszik megközelíteni

B

-t, hogy a kisebb

T B

távolság maradjon úszásra. A matematikai számítás azt eredményezi, hogy akkor ér

A

legrövidebb idő alatt

B

-hez, ha úgy választja a

T

pontot, hogy

\begin{matrix} c_{1} : c_{2} = sin α : sin β; \end{matrix}

(1)

ahol

α

a futási,

β

az úszási iránynak a merőlegessel alkotott szöge.

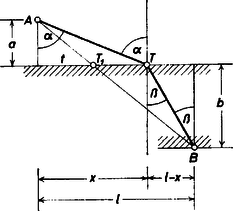2. ábra

Ugyanis a 2. ábra szerint a futási idő

t_{1} = \sqrt[]{a^{2} + x^{2}} / c_{1}

, az úszási idő

t_{2} = \sqrt[]{b^{2} + {(l - x)}^{2}} / c_{2}

. Az összes idő

\begin{matrix} y = t_{1} + t_{2} = \sqrt[]{a^{2} + x^{2}} / c_{1} + \sqrt[]{b^{2} + {(l - x)}^{2}} / c_{2} \\ \frac{d y}{d x} = \frac{x}{c_{1} \sqrt[]{a^{2} + x^{2}}} - \frac{l - x}{c_{2} \sqrt[]{b^{2} + {(l - x)}^{2}}} = 0, \end{matrix}

amiből már a fenti arányosság következik.
A fény ugyanezen szabály szerint ,,választja meg'' a

T

töréspontot, amikor egy optikailag ritkább közegből belép egy optikailag sűrűbb közegbe, (melyben a sebessége már csökken).
Hasonló gondolatok jutottak eszembe, amikor megpillantottam azt a négyes ikrek cseresznyeszemet, melyre régi kedves barátom, Borsodi Sándor tőszomszédom hívta fel figyelmemet (3. és 3/a ábra).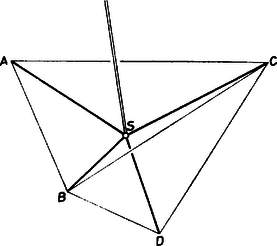

3/a. ábra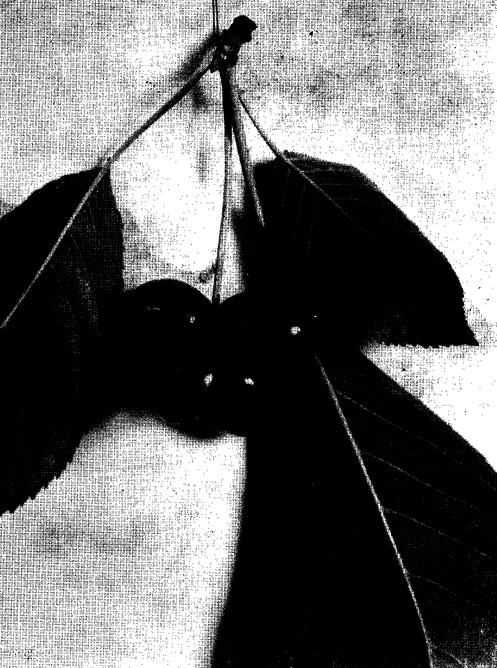

3. ábra

Ha a cseresznyeszemeket gömböknek képzeljük, akkor felvetődik az a kérdés, hogy négy gömb sokféle elhelyezkedési lehetősége közül mi jellemző éppen a keletkezett, és bizonyára még nagyon kevés ember által látott ilyen négyes cseresznyeikrekre.
Tételezzük fel, hogy megvizsgálandó, mikor lesz legkisebb a cseresznyeszár végének a gömbfelszínektől mért távolságösszege.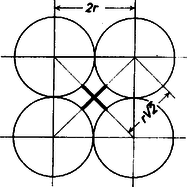

4. ábra

Ha a négy gömb középpontjai egy négyzet csúcspontjaiban helyezkednének el (4. ábra), akkor a középponttól mért távolságok összege

\begin{matrix} 4 (r \sqrt[]{2} - r) = 4 r (\sqrt[]{2} - 1) \approx 4 \cdot 0, 41 r \approx 1, 64 r \end{matrix}

lenne.
Lássuk továbbá azt az esetet, amikor a gömbközéppontok olyan rombusz csúcspontjaiban helyezkednek el, melyet a rövidebb átlója két egyenlő oldalú háromszögre oszt (5. ábra).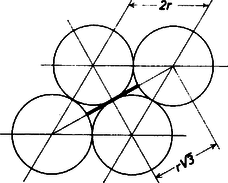

5. ábra

2 r

oldalhosszúságú egyenlő oldalú háromszög magassága

\begin{matrix} h = r \sqrt[]{3} . \end{matrix}

(2)

Mivel most két gömb érintkezik egymással, a szár végpontjának a másik két gömb felszínétől mért összege

\begin{matrix} 2 (r \sqrt[]{3} - r) = 2 r (\sqrt[]{3} - 1) \approx 2 \cdot 0, 73 r \approx 1, 46 r . \end{matrix}

Lássuk most azt a harmadik esetet, mely legjobban megközelíti a valóságban létrejött négyes ikertermést. A négy gömb középpontja egy szabályos tetraéder (6/a ábra) csúcspontjaiban helyezkedik el.
Legyen a tetraéder élének hossza

\begin{matrix} A B = B C = C A = A D = B D = C D . \end{matrix}

Szabályos háromszögeinek magassága (2) szerint

\begin{matrix} A A_{1} = D A_{1} = h = r \sqrt[]{3} . \end{matrix}

A 6/b ábra szerint

A_{1} B_{1} ∥ A B

, tehát

\begin{matrix} A B O_{1} ▵ \sim A_{1} B_{1} O_{1} ▵, \end{matrix}

és így

\begin{matrix} A O_{1} : O_{1} A_{1} = A B : A_{1} B_{1} = A C : B_{1} C = 2 : 1, \end{matrix}

vagyis

\begin{matrix} A O_{1} = 2 O_{1} A_{1}, \end{matrix}

tehát

\begin{matrix} A A_{1} = A O_{1} + O_{1} A_{1} = 3 O_{1} A_{1}, \end{matrix}

vagyis

\begin{matrix} O_{1} A_{1} = A A_{1} / 3 = r \sqrt[]{3} / 3. \end{matrix}

A tetraéder

m

magasságát az

O_{1} A_{1} D

derékszögű háromszögből kapjuk meg (6c ábra).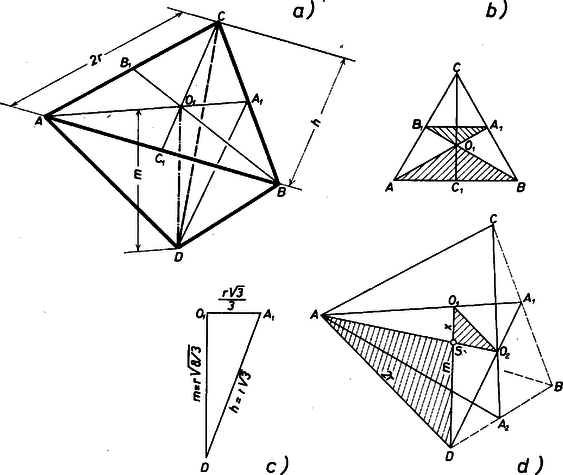

\begin{matrix} m = \sqrt[]{D A_{1}^{2} - O_{1} A_{1}^{2}} = \sqrt[]{3 r^{2} - 1 / 3 r^{2}}, \\ m = r \sqrt[]{\frac{8}{3}} \approx 1, 633 r . & (3) \end{matrix}

6. ábra

A tetraéder valamely lapjának oldalfelezői a szemközti negyedik csúcsponttal olyan síkokat határoznak meg, melyek mindegyike tartalmazza a tetraéder

S

súlypontját. Ilyen sík

4 \cdot 3 = 12

van, de elegendő ezek közül két olyat tekintetbe venni, melyek a tetraéder

m

magasságát is tartalmazzák, hogy az

S

súlypont helyét meghatározzuk. A 6d ábrán az

A B C

háromszög

A A_{1}

szögfelezőjéhez tartozó

A A_{1} D

háromszöget és

A B D

háromszög

A A_{2}

szögfelezőjéhez tartozó

A A_{2} C

háromszöget vettük figyelembe. Az ábra jelöléseivel

A_{1} O_{1} = A_{1} O_{2} = h / 3

, tehát

O_{1} O_{2} ∥ A D

, ennélfogva

\begin{matrix} S O_{1} O_{2} ▵ \sim S D A ▵ . \end{matrix}

Az ábra jelöléseivel

O_{1} S = x

, és az

A_{1} O_{1} O_{2} ▵ \sim A_{1} A D ▵

hasonlóság alapján

O_{1} O_{2} = 2 r / 3

\begin{matrix} O_{1} S : O_{1} O_{2} = S D : A D, \end{matrix}

vagyis

\begin{matrix} x : 2 r / 3 = (m - x) : 2 r, \end{matrix}

ahonnan

\begin{matrix} x = m / 4, \end{matrix}

(4)

vagyis a súlypont távolsága az oldallapoktól (4) szerint (3) tekintetbe vételével

\begin{matrix} x \approx 1, 633 r / 4 \approx 0, 408 r, \end{matrix}

és a súlypont távolsága a csúcsoktól

\begin{matrix} m - x \approx r (1, 633 - 0, 408) \approx 1, 225 r . \end{matrix}

Ha a szár

S

pontban végződik, akkor kb.

(1, 225 - 1) r = 0, 225 r

távolságra közelíti meg az egyes gömbök felszínét. Ennek a négyszerese

0, 9 r

, tehát a legkisebb a megvizsgált elhelyezkedési lehetőségek között. Kb.

12

mm-es szemátmérőnél ez a távolság

1, 2

mm; ezt a távolságot egyrészt a cseresznye gömbtől eltérő alakja, másrészt a szárvég kiszélesedése annyira kiküszöböli, hogy valóságban a táplálékot közvetítő szárnak a vége mind a négy gyümölcsszemmel érintkezik.
A kettős ikerképződmény sokkal gyakoribb, sőt ezeknél a magvak összenövésével is találkozunk. Ilyen ikermandulamagvat tüntet fel a 7. ábra.

7. ábra

Erről világosan látható, hogy a táplálékot közvetítő szár lehetőleg egyformán érintkezik mind a két ikerszemmel.
A 6. és 7. ábrák alapján már sejthetjük a hármas ikerszem geometriai formáját. A szemeket újra gömb alakra egyszerűsítve, vizsgáljuk azt az esetet, amikor az ikerszemek csak húsaikkal nőttek össze, de a magvak még különváltak. A 8a ábrán láthatjuk, ennek az a feltétele, hogy a középpontok egymástól való távolsága

\begin{matrix} 2 \sqrt[]{r^{2} - ϱ^{2}} = 2 h = O_{1} O_{2} \end{matrix}

(5)

nagyobb legyen, mint a mag átmérője.
A 8a ábrán felülnézetben, a 8b ábrán elölnézetben látható a hármas ikerszem.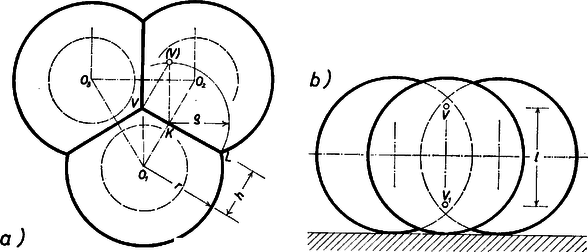

8. ábra

A gömbök középpontjai az

O_{1} O_{2} O_{3}

egyenlő oldalú háromszög csúcspontjai. A keletkezett három

ϱ

sugarú áthatási kör síkja egy olyan

V V_{1}

egyenesközt tartalmaz, melynek

V

végpontjában végződik az egyetlen szár.
A

V V_{1} = l

fél hosszát a

ϱ

sugarú körben határozhatjuk meg. A 8a ábra jelöléseivel

O_{1} L = r

;

K L = ϱ

;

O_{1} K = h

és

\begin{matrix} V K = h \cdot tg 30^{\circ} = \sqrt[]{r^{2} - ϱ^{2}} / \sqrt[]{3} . \end{matrix}

(6)

A térbeli

V

pontnak a gömbközéppontok síkjába való beforgatását

(V)

-vel jelölve, a

ϱ

sugarú kör

K V (V)

derékszögű háromszögének

V (V)

befogója a keresett hossz az (5) és (6) kifejezésének felhasználásával

\begin{matrix} V (V) = l / 2 = \sqrt[]{ϱ^{2} - V K^{2}} = \sqrt[]{ϱ^{2} - (r^{2} - ϱ^{2}) / 3} = \sqrt[]{(4 ϱ^{2} - r^{2}) / 3.} \end{matrix}