Kezdőlap


Cím:	1974. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):	Surányi János
Füzet:	1975/február, 51 - 59. oldal	PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat.

Egy könyvtár ki- és bejáratánál egy-egy tábla áll. Minden be-, illetve kilépőnek fel kell írnia a megfelelő táblára, hogy hány embert talált, illetve hagyott a könyvtárban.
Bizonyítsuk be, hogy egy teljes nap során ugyanazok a számok kerülnek a két táblára, legfeljebb más sorrendben (feltesszük, hogy egyszerre csak egy ember érkezik vagy távozik).

Az egyik versenyző (Hajdu István, Hódmezővásárhely) megoldását igen szemléletes, hangulatos formában fogalmazta meg. Elsőnek ezt közöljük eredeti alakjában.

I. megoldás. Ha valaki bemegy a könyvtárba, akkor ezután két olyan dolog történhetik meg, amely a feladat szempontjából lényeges. Vagy eszébe jut, hogy otthon hagyta az olvasójegyét és távozik, mielőtt egy másik ember bejönne, ‐ ekkor nyilvánvaló, hogy ugyanannyi embert hagy ott, mint amennyit talált, ‐; vagy ottmarad, és ez esetben újak érkeznek utána, az olvasók száma nő a polcok között.
A második esetet vizsgáljuk meg közelebbről!
Miután könyvtárunk úgyis különleges tulajdonságokkal rendelkezik, olvasói bizonyára elfogadják a következő módosítást, amely a feladat szempontjából közömbös: miután az egyes személyek nincsenek kitüntetve, teljesen mindegy, hogy adott pillanatban ki lép be vagy ki hagyja el a termet, ezért tehát megállapodhatunk abban, hogy mindig az menjen el, aki utoljára bejött. Például: fessünk az egyik béketűrő olvasó hátára egy nagy vörös ,,

A

'' betűt. ,,

A

'' bejön, felírja, hogy

n

db embert talált az olvasóteremben. Ezután leül, közben jönnek-mennek a többiek. Tegyük fel, hogy

k

db olvasó érkezett még. Egyszercsak ,,

A

'' feláll és elindul az ajtó felé. Ekkor azonban elébe állunk és megkérjük, hogy maradjon még. Helyette elküldjük azt, aki legutóbb bejött, akinek a száma,

(n + k)

, a belépő tábla legalján van. A feladat szempontjából teljesen közömbös, hogy ,,

A

'' barátunk egész nap ott rostokol, hiszen egy főt elzavartunk helyette. Tettük ezt pedig oly módon, hogy minden távozó ugyanazt a számot írta fel a távozási táblára, mint a másikra, amikor bejött. Ha egy idő múlva már senki sem jön többé olvasni, akkor kiengedjük a bennszorultakat érkezésük fordított sorrendjében. Így sor kerül szegény ,,

A

''-ra is, aki önkényünk áldozata lett, majd többi társára, míg végül senki sem marad benn. Így tehát minden olvasóhoz egy számpárt rendeltünk hozzá egy-egyértelműen. Miután a feladat szempontjából lényeges változtatást nem tettünk, ugyanazt az eredményt kell kapnunk, mint egyébként, vagyis a két táblán ugyanazok a számok szerepelnek (noha más-más sorrendben).

II. megoldás. Módosítsuk az előírást a következőképpen: aki eltávozik, a bejárati táblán áthúzza a könyvtárban maradó olvasók számát, ha az szerepel ott áthúzatlanul; ha nem szerepel, akkor felírja a kijárati táblára. Nem nehéz belátni, hogy az utóbbira sohasem kerül sor, ha ugyanis

k

olvasó tartózkodik a könyvtárban, akkor a táblán (áthúzatlanul) a

0,1, ..., k - 1

számok szerepelnek egyszer-egyszer. Speciálisan, ha nincs bent senki, akkor a tábla is üres. Megmutatjuk, hogy ez a helyzet minden létszámváltozásnál érvényben marad.
Nyitáskor az utoljára említett helyzet áll fenn.
Ha egy időpontban a leírt helyzet fennáll és valaki érkezik a könyvtárba, akkor a létszám

(k + 1)

-re nő, és ugyanakkor a táblára a

0,1, ..., k - 1

számok mellé odakerül a

k

is.
Ha viszont valaki eltávozik, akkor

(k - 1)

olvasót hagy a teremben és ennek megfelelően áthúzza a

(k - 1)

-et, tehát a

0,1, ..., (k - 2)

marad a táblán egy-egy példányban.
Záráskor senki sem marad a teremben, ennek megfelelően a bejárati táblán is minden szám át lesz húzva. Ez annak felel meg, hogy az eredeti előírás szerint a kijárati táblára ugyanazok a számok kerülnek, mint a bejáratira.

Megjegyzések. Sokféleképpen fogalmazták a versenyzők a megoldást, bár az alapgondolat hasonló a fentiekhez. Röviden említünk néhányat.

1. Többen egy embert állítottak egy létra elé, aki minden időben a létra annyiadik fokán áll, ahányan a könyvtárban vannak. Emberünk egyenként lép feljebb vagy lejjebb. Ahányadik fokról felfelé lép, az a szám kerül a bejárati táblára, ahányadikra lefelé lép, az a kijáratira. A feladat állításának helyessége abból következik, hogy minden fokról ugyanannyiszor lépett felfelé, ahányszor lefelé jövet rálépett, mert estére földet ér és hazamegy.
2. Egy koordinátarendszer

x

tengelyén egyenlő távolságban sorakozó pontok feleljenek meg az egymás utáni létszámváltozások időpontjának, és ábrázoljuk az

y

tengely irányában a létszámot. A kapott pontokat összekötő törtvonal és az

x

tengely egy vagy több zárt sokszöget alkot. Ezt

k

és

(k + 1)

magasság közt az

x

tengellyel párhuzamosan átmetszve, a metsző egyenes ugyanannyiszor lép be a sokszögbe, mint ahányszor kilép belőle, azaz ugyanannyi emelkedő és süllyedő szakaszt metsz át. Az előbbiek alsó végpontja, azaz esetünkben

k

jelöli a bejárati táblára kerülő számot, a süllyedők alsó végpontja a kijárati táblára kerülőkét. Előbb tett megjegyzésünk szerint a kettő egyenlő.
3. Írjunk le

(+ 1)

-et, valahányszor érkezik valaki, és

(- 1)

-et, valahányszor távozik. Ekkor bármelyik számig összeadva számainkat, az illető számnak megfelelő érkezés, ill. távozás után kialakult olvasólétszámot kapjuk. Ez az összeg nem lehet negatív, vagyis a sorozat bármelyik számáig legalább annyi

(+ 1)

van, mint

(- 1)

, az egész sorozatban pedig ugyanannyi van mindkettőből. A bejárati táblára az egyes

(+ 1)

-ek előtti számig terjedő összegek kerülnek, a kijárati táblára pedig a

(- 1)

-ekig terjedő összegek [ezt a

(- 1)

-et is még beleértve]. Most abból következik az állítás helyessége, hogy egy egymást követő

(+ 1, - 1)

párnak megfelelően ugyanaz a szám kerül a két táblára, ha pedig ezt a párt kihagyjuk a sorozatból, akkor a sorozat leírt szerkezete nem változik meg.

Második feladat.

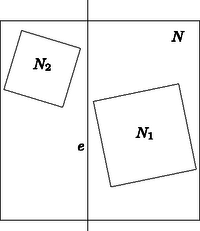
Adott négyzeteknek egy végtelen sorozata, az oldalak hossza rendre

1,

1 / 2,

1 / 3,

...,

1 / n,

... .

Bizonyítsuk be, hogy van olyan négyzet, amelyben mindezek átfedés nélkül elhelyezhetők, és keressük meg a legkisebb ilyen négyzetet.

Külön tárgyaljuk a feladat két részét: először megmutatjuk, hogy elhelyezhetők négyzeteink egy 1,5 oldalhosszúságú négyzetben, azután bebizonyítjuk, hogy kisebb oldalú négyzetben már az 1 és a 0,5 oldalhosszúságú négyzet sem helyezhető el átfedés nélkül.
a) Az összes négyzetek elhelyezése 1,5 oldalhosszúságú négyzetben:

I. megoldás. Helyezzük egymás mellé az

1 / 3^{k}

oldalú négyzettől az

1 / (3^{k + 1} - 1)

oldalúig valamennyit, ahol

k = 0,1, ...

. Közülük az első

3^{k}

négyzet oldalának a hossza nem nagyobb

1 / 3^{k}

-nál, a következő

3^{k}

-é pedig

1 / (2 \cdot 3^{k})

-nál, így a keletkező sor hossza nem nagyobb, mint

\begin{matrix} 3^{k} \cdot (1 / 3^{k} + 1 / (2 \cdot 3^{k})) = 1, 5. \end{matrix}

Helyezzük a keletkező sorokat egymás fölé. Mindegyikben az első négyzet a legmagasabb, így az összes sorok magassága együtt

\begin{matrix} \frac{1}{3^{0}} + \frac{1}{3^{1}} + \frac{1}{3^{2}} + ... = \frac{1}{1 - \frac{1}{3}} = 1, 5. \end{matrix}

II. megoldás. Helyezzük az

1

oldalú négyzet mellé az

1 / 2

és

1 / 3

oldalút, majd fölé az

1 / 4

1 / 5

1 / 6

és

1 / 7

oldalút, a továbbiakban pedig mindegyik négyzetre a fele akkora oldalút és a rákövetkezőt.
Az utóbbi kettő nyilván nem nyúlik túl az alattuk levő négyzeten, és

\begin{matrix} \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} < 4 \cdot \frac{1}{4} = 1 \end{matrix}

folytán az első négy négyzet sem az

1

oldalú négyzeten.
Az

1 / k

oldalú négyzet

(k = 4,5,6,7)

és a ráhelyezettek felfelé nem nyúlnak magasabbra, mint

\begin{matrix} \frac{1}{k} + \frac{1}{2 k} + \frac{1}{4 k} + \frac{1}{8 k} + ... = \frac{2}{k} \leq \frac{1}{2}, \end{matrix}

így négyzeteinket elhelyeztük egy 1,5 oldalú négyzetben.
Megjegyzés. A versenyzők nagy része először a négyzetek területösszegét becsülte meg felülről, sőt néhányan azt is tudták, hogy a területek alkotta végtelen sor összege^{$^{*}$}

\frac{π^{2}}{6}

. Az összeg megbecslése fölösleges már azért is, mert a négyzetek elhelyezése már ad egy ilyen felső becslést, hiszen a befoglaló négyzet területe,

2, 25

, felső korlát.
A második megoldás érdekessége az, hogy meglepően jó felső korlátot lehet belőle leolvasni. Valóban, a megoldás végén azt nyertük, hogy az

1 / k

oldalú négyzet és a ráhelyezettek benne vannak egy

2 / k

1 / k

oldalú téglalapban

(k = 4,5,6,7)

, így az összes négyzetek együttes területe nem nagyobb, mint

\begin{matrix} 1 + \frac{1}{4} + \frac{1}{9} + 2 (\frac{1}{16} + \frac{1}{25} + \frac{1}{36} + \frac{1}{49}) < 1, 663, míg \frac{π^{2}}{6} = 1, 6449 ... \end{matrix}

b) Az

1

és a

0, 5

oldalú négyzet nem helyezhető el átfedés nélkül

1, 5

-nél kisebb oldalú négyzetben.

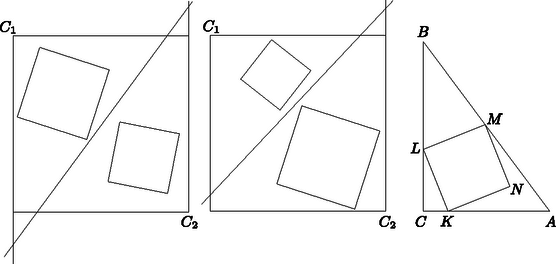
I. megoldás. Helyezkedjék el az

1

oldalú

N_{1}

és az

1 / 2

oldalú

N_{2}

négyzet egy

N

négyzetben úgy, hogy ne legyen közös belső pontjuk. Ekkor van olyan

e

egyenes, amelynek

N_{1}

és

N_{2}

ellenkező oldalán fekszik. Ha

e

párhuzamos

N

valamelyik oldalával, akkor két téglalapra bontja azt, és mindegyiknek az

e

-re merőleges oldala legalább akkora, mint a sávban fekvő négyzet oldala. Ez esetben tehát

N

oldala legalább akkora, mint

N_{1}

és

N_{2}

oldalának összege.

1. ábra

e

metszi

N

mindegyik oldalegyenesét, akkor vegyük mindkét oldalán

N

-nek a tőle legtávolabbi

C_{1}

, ill.

C_{2}

csúcsát. A

C_{1}

-en, ill.

C_{2}

-n átmenő oldalegyenesek

e

-vel egy

H_{1}

, ill.

H_{2}

derékszögű háromszöget alkotnak, amelyik

N_{1}

-et, ill.

N_{2}

-t tartalmazza. Állításunk bizonyítására elég azt megmutatni, hogy egy derékszögű háromszög tartalmazta négyzetek közül az a legnagyobb, amelyiknek két oldala a háromszög befogóin nyugszik, egy csúcsa pedig az átfogón van.
Valóban, ha ez igaz, akkor a

H_{1}

-ben és

H_{2}

-ben elhelyezhető legnagyobb négyzet átlója,

N

-nek a

C_{1} C_{2}

átlójára esik, és mivel a négyzetek nem fedhetik át egymást, így átlóik összege

N

átlóját, oldalhosszaik összege tehát

N

oldalát adja, vagyis igaz a bizonyítandó állítás is.
A továbbiakban a fent megfogalmazott segédtételt bizonyítjuk.
Az

A B C

derékszögű háromszögben levő tetszés szerinti

K L M N

négyzetet elmozgathatjuk úgy, hogy két csúcsa, mondjuk

K

és

L

A C

, ill.

B C

befogón legyen ‐ ha nem lett volna így eredetileg ‐, majd

C

-ből nagyítva, ha kell, elérhetjük, hogy egy csúcs az átfogóra kerüljön. Elég tehát az ilyen helyzetű négyzeteket vizsgálni. Ezek középpontja a háromszög derékszögének szögfelezőjén van. Forgassuk el ugyanis a négyzetet a középpontja körül derékszöggel úgy, hogy az

A C

-n levő csúcsa a

B C

-n levőbe menjen át. Ekkor az

A C

egyenes is átmegy

B C

-be, így a középpont e két egyenestől egyenlő távolságban van, tehát rajta van a köztük levő szög felezőjén.

2. ábra

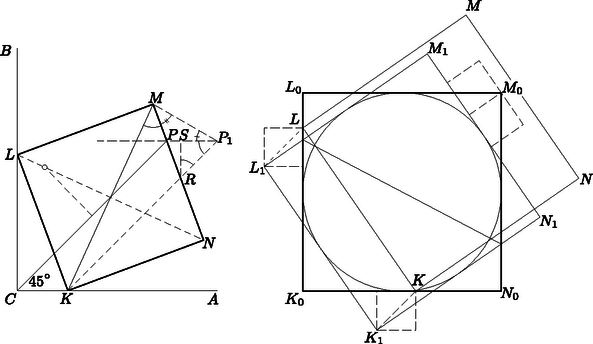3. ábra

Annak a négyzetnek, amelyiknek az egyik csúcsa

C

-be esik, az ezzel szemközti csúcsa nincs közelebb

C

-hez, mint a

C

-ből induló szögfelező

M N

-nel való

P

metszéspontja. Elég tehát megmutatnunk, hogy ha

K

és

L

különbözik

C

-től, akkor

C P > K M

.
Toljuk el

C P

-t párhuzamosan a

K P_{1}

helyzetbe, ekkor a

K P_{1} M

háromszög két oldalát kell összehasonlítanunk. Ezt a velük szemben levő szögek közvetítésével fogjuk megtenni. A

K M

-mel, ill.

K P_{1}

-gyel szemközti szög

P P_{1} M ∢

-gel, ill.

P M P_{1} ∢

-gel nagyobb

45^{\circ}

-nál.
Jelöljük

K P_{1}

és

M N

metszéspontját

R

-rel,

R

vetülete

P P_{1}

-en legyen

S

P_{1} R S

háromszög derékszögű és egyenlő szárú, továbbá

S

P

és

P_{1}

pont közt van, így

\begin{matrix} P R P_{1} ∢ > S R P_{1} ∢ = P P_{1} R ∢, \end{matrix}

amiből következik, hogy

\begin{matrix} P P_{1} > P R . \end{matrix}

Azt is tudjuk, hogy

C P

felezi

K M

-et, így felezi

M R

-t is, mert

K R

és

C P

párhuzamos. Ezért

\begin{matrix} M P = P R < P P_{1}, tehát M P_{1} P ∢ < P M P_{1} ∢ . \end{matrix}

De ekkor egyszersmind

\begin{matrix} M P_{1} K ∢ = M P_{1} P ∢ + 45^{\circ} < P M P_{1} ∢ + 45^{\circ} = K M P_{1} ∢, \end{matrix}

amiből viszont

\begin{matrix} K M < K P_{1} = C P \end{matrix}

következik, és ezt akartuk bizonyítani.

Megjegyzés. Gyorsabban befejezhetjük a bizonyítást a kerületi szögek tételének felhasználásával:

C

K

P

és

M

egy körön van, mert

K P