Cím: Megjegyzések az 1973. évi Kürschák József-verseny 3. feladatához
Szerző(k):  Lovász László 
Füzet: 1975/január, 1 - 5. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szóban forgó feladat így szólt:

 

Adott a térben n sík (n≥5) úgy, hogy bármelyik háromnak pontosan egy közös pontja van és nincs a térnek olyan pontja, amelyen közülük háromnál több menne át.
Bizonyítsuk be, hogy azon térrészek között, melyekre a síkok a teret darabolják, legalább 2n-34 tetraéder van.
 

A megoldásokat ismertető cikkben* felvetettük a kérdést, hogy mennyire éles a 2n-34-es korlát; nem helyettesíthető-e jobbal? A válasz igenlő; körülbelül versenyünkkel egy időben R. W. Shannon fiatal amerikai matematikus kimutatta, hogy:
 

1. tétel. Ha n sík (n≥4) a feladatban tett kikötéseknek eleget tesz, úgy az általuk létrehozott térrészek között legalább (n-3) tetraéder van.
Valójában a fenti állítás története bonyolultabb. Hogy megértsük, tekintsünk először egy egyszerűbb esetet, a síkbeli egyenesek esetét. Legyenek e1,e2,...,en síkbeli egyenesek (n≥3), melyek közül nem megy át három egy ponton és melyek között nincsenek párhuzamosak. Hány háromszög van legalább az általuk létrehozott síkrészek között? A versenyfeladat megoldását követve láthatjuk, hogy legalább 2n-23 (hacsak n≥4); vizsgáljuk meg, állíthatunk-e többet?
Az n=3 és 4 esetekben lényegében* csak egyféleképpen helyezhetünk el n egyenest, ezeket az elhelyezéseket az 1. ábra mutatja.
 

 

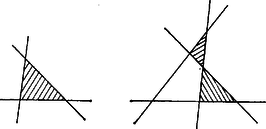1. ábra
 

A háromszögek száma 1, ill. 2. Az n=5 esetre már 6 lényegesen különböző elrendezése van az egyeneseknek; mindegyikben legalább 3 háromszöget számolunk (2. ábra).
 

 

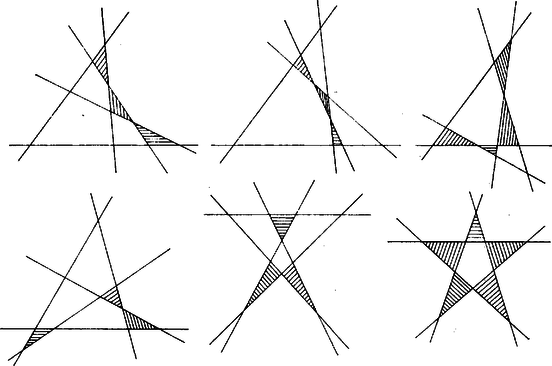2. ábra
 

Ha 6 egyenesnek felrajzoljuk néhány elhelyezését, mindig legalább 4 háromszöget találunk (3. ábra).
 

 

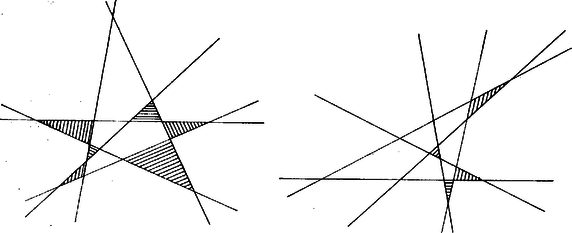3. ábra
 

Ezek a számadatok azt sugallják, hogy:
 

2. tétel. Ha n egyenes úgy helyezkedik el a síkban, hogy semelyik három nem halad át egy ponton és semelyik kettő sem párhuzamos, akkor azon síkrészek között, melyekre az egyenesek a síkot darabolják, legalább (n-2) háromszög van.
Ezt az állítást, valamint térbeli megfelelőjét, melyet fent idéztünk, S. Roberts fogalmazta meg 1889-ben. Bizonyítása azonban annyira vázlatos volt, hogy azt nem sikerült teljessé tenni; Branko Grünbaum néhány évvel ezelőtt megoldatlan problémaként említette ezt. R. W. Shannon munkája a síkbeli és térbeli problémára egyaránt választ ad; bizonyítása azonban olyan eszközöket használ, melyeket itt nem ismertethetünk. Így arra fogunk szorítkozni, hogy egy rokon probléma megoldását bemutassuk, (melyhez hasonló lépések, és még sok más, Shannon bizonyításában is szerepelnek).
Először is megjegyezzük, hogy van n egyenes a síkban, melyek között nincsenek párhuzamosak és semelyik három nem megy át egy ponton, és melyek pontosan (n-2) háromszöget határoznak meg.
Tekintsük ugyanis egy k kör n különböző érintőjét, melyek egyazon félkörívet érintenek (4. ábra). Ezek az egyenesek nyilván nem párhuzamosak és nem halad át semelyik három egy ponton.
 

 

4. ábra
 

Az olvasóra bízzuk annak igazolását, hogy ekkor pontosan (n-2) háromszögtartomány keletkezik.
Módosítsuk most feladatunkat úgy, hogy tekintsük háromszögnek a szögtartományokat is. Hány, ilyen értelemben vett "háromszög'' lesz akkor? n=3,4,5-re azt találjuk, hogy legalább 4, 5, 6; sejthetjük tehát, hogy
 

3. tétel. Ha n(≥3) egyenes között nincs két párhuzamos és három egy ponton átmenő, akkor azon síkrészek között, melyekre a síkot osztják,a háromszögek és szögtartományok együttes száma legalább (n+1).
Hogy viszonylik ez az állítás a 2. tételhez? A 2. tétel szerint van legalább (n-2) háromszög; meg fogjuk mutatni, hogy van legalább 3 szögtartomány. Így a 2. tételből következik a 3. tétel. Itt most megmutatjuk, hogy a 3. tétel közvetlenül is bizonyítható.
 
4. tétel. A 3. tétel feltételeivel a síkrészek között legalább 3 szögtartomány van.
 

Bizonyítás. Tekintsük az egyenesek összes metszéspontjainak halmazát és ennek konvex burkát. Ez konvex sokszög, így legalább 3 csúcsa van (hiszen a metszéspontok nem lehetnek mind egy egyenesen). Legyen P egy csúcsa a konvex buroknak és a, b azon két egyenes, melyek P-ben metszik egymást.
Mármost a-nak P által határolt két félegyenese közül az egyiken nincs további metszéspont, különben P nem lehetne csúcsa a konvex buroknak; legyen ez a1. Ugyanígy, b-nek valamelyik, P által határolt b1 félegyenesét sem metszi további egyenes. Ekkor az a1 és b1 által alkotott konvex szögtartományba a többi (n-2) egyenes nem metsz bele; ez a szögtartomány tehát egyike a tekintett síkrészeknek (5. ábra).
 

 

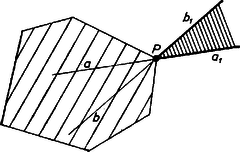5. ábra
 

Így a konvex burok minden csúcsához illeszkedik egy olyan síkrész, mely szögtartomány; az ilyen síkrészek száma tehát legalább 3.
 

Hasonló gondolatmenettel bizonyítható állításunk térbeli megfelelője:
 

5. tétel. Ha n(≥4) sík közül bármely háromnak van közös pontja és semelyik négy nem halad át egy ponton, a síkok által létrehozott térrészek között legalább 4 triédertartomány (három szögtartomány által határolt térrész, "térszög'') van.
A 3. tétel bizonyítása előtt egy segédtételt igazolunk:
 

Segédtétel: Az adott egyenesek mindegyikére legalább három olyan síkrész illeszkedik, mely háromszög vagy sokszögtartomány.
Bizonyítás. Legyenek e1,...,en, a tétel feltételeit kielégítő egyenesek az S síkban; megmutatjuk, hogy pl. e1-re legalább három háromszög, ill. szögtartomány illeszkedik. A bizonyítás alapgondolata az, hogy ha az adott egyeneseket egy másik síkra vetítjük úgy, hogy az e1 egyenes a "végtelenbe'' kerüljön, akkor az e1-re illeszkedő háromszögek és szögtartományok az új egyenesek alkotta szögtartományoknak fognak megfelelni. Ez utóbbiakról már tudjuk, hogy számuk legalább 3.
Legyen tehát S' olyan sík, mely S-et e1-gyel párhuzamos e'1 egyenesben metszi; legyen fe1-gyel párhuzamos egyenes S'-ben. Fektessünk e1-en át S'-vel és f-en át S-sel párhuzamos síkot; legyen P ezek metszésvonalának egy pontja.
Vetítsük mármost az e2,...,en egyeneseket P-ből S'-re; legyenek f2,...,fn a kapott egyenesek. Ekkor megállapíthatjuk, hogy
 

(a) az f,f2,...,fn egyenesek között nincsenek párhuzamosak;
(b) az f,f2,...,fn egyenesek közül nem megy át három egy ponton;
(c) ha e1, ei, ej (1<i<j≤n) olyan háromszöget alkotnak, melybe további ek egyenesek nem metszenek bele, akkor fi, fj ilyen tulajdonságú szögtartományt határol és viszont;
(d) ha e1, ei olyan szögtartományt határol, amelybe másik ek nem metsz bele, akkor f, fi ugyanilyen tulajdonságú szögtartományt határol (6. ábra).
 

 

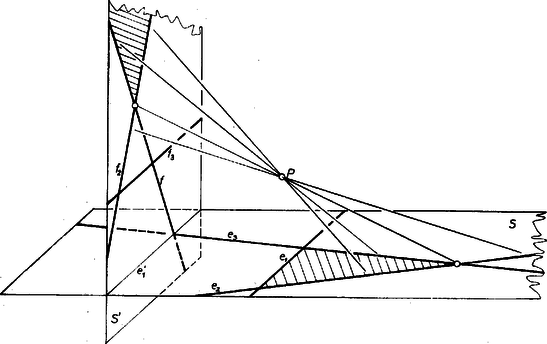6. ábra
 

Ezen állítások igazolását az olvasóra hagyjuk. A fenti megfigyelésekből láthatjuk, hogy f,f2,...,fn, legalább 3 szögtartományt hoz létre a 4. tétel szerint. Mivel (c), (d) szerint ezen szögtartományok mindegyikének megfelel az S síkon egy e1-re illeszkedő háromszög vagy szögtartomány, és ily módon az utóbbinak száma legalább három. Ezzel a segédtételt igazoltuk.
 

A 3. tétel mármost egyszerű számolással adódik. Az n egyenes mindegyikére illeszkedik, a segédtétel alapján, legalább 3 háromszög vagy szögtartomány; így legalább 3n háromszöget és szögtartományt számolunk. Persze, minden ilyen síkrészt többször is számoltunk; a háromszögeket mindhárom oldalegyenesüknél, tehát 3-szor; a szögtartományokat két határoló egyenesüknél, tehát 2-szer. Számoljuk ezért hozzá még egyszer a szögtartományokat; így már (3n+3) szögtartományt és háromszöget számolunk legalább. A (3n+3)-at még 3-mal osztani kell, hogy a háromszögek és szögtartományok számára alsó korlátot kapjunk. Tehát ez a szám legalább 3n+33=n+1. Ezzel a 3. tételt bebizonyítottuk.
Végül, hogy valamelyest érzékeltessük R. W. Shannon bizonyításának menetét, tekintsünk 6 egyenest a síkban. Shannon ekkor konstruált 6 síkot a térben úgy, hogy az egyenesek által alkotott háromszögek a síkok által alkotott triédertartományoknak feleljenek meg. Így az 5. tételből nyeri a 2. tétel állítását 6 egyenesre.
A konstrukció leírása és n egyenesre való általánosítása azonban az ún. többdimenziós geometria eszközeit igényli, és így nem fér bele e cikk kereteibe. Az 1. és 2. tételre elemi (vagyis a sík-, ill. térgeometria körében elvégezhető) bizonyítás nem ismeretes, ami a tételek egyszerű alakját tekintve igen meglepő. Ilyen bizonyítást találni igen érdekes volna.
*Surányi János-Lovász László: Az 1973. évi Kürschák József matematikai tanulóverseny feladatainak megoldása, K. M. L. 48 (1974) 49-55. oldal.

*Ezen azt értjük, hogy n (= 3, 4) egyenes két különböző elhelyezése esetén az egyik elhelyezés egyenesei, ill. síkrészei megfeleltethetők (kölcsönösen egyértelműen) a másik elhelyezés egyeneseinek, ill. síkrészeinek úgy, hogy a megfelelő síkrészeket a megfelelő egyenesek határolják.