Kezdőlap


Cím:	Az 1974. évi (7.) Nemzetközi Fizikai diákolimpia feladatai
Szerző(k):	Meszéna Géza
Füzet:	1974/november, 161 - 164. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. feladat. Egy nyugalomban és alapállapotban levő hidrogénatomnak nekiütközik egy másik alapállapotban levő hidrogénatom. Mekkora az a legkisebb sebesség, amelynél az ütközés már nem rugalmas? Ha ennél nagyobb az ütközési sebesség és fénykibocsátásra kerül sor, akkor ezt a fényt a kezdeti sebesség irányából és azzal ellentétes irányból figyeljük meg. Mennyi ezek rezgésszámainak viszonylagos eltérése a tényleges rezgésszámhoz képest? A hidrogénatom tömege $1, 67 \cdot 10^{- 27} kg$ , ionizációs energiája $E = 13, 6 eV = 2, 18 \cdot 10^{- 18} joule$ .

Megoldás. Alapállapotban a hidrogénatom energiája

E_{1} = - E \cdot \frac{1}{1^{2}}

, az első gerjesztett állapotban

E_{2} = - E \cdot \frac{1}{2^{2}}

. A hidrogénatom által felvehető legkisebb energiaadag:

\begin{matrix} E_{2} - E_{1} = E (\frac{1}{1^{2}} - \frac{1}{2^{2}}) = \frac{3}{4} \cdot E = 1, 635 \cdot 10^{- 18} joule = Δ E . \end{matrix}

Keresnünk kell azt a legkisebb sebességet, amelynél az ütközés energiavesztesége elérheti ezt az értéket. Mivel az ütközési energiaveszteség akkor a legnagyobb, ha az ütközés teljesen rugalmatlan, az ütközés utáni közös sebesség

v / 2

lesz. A kezdeti és végső mozgási energiák különbsége

(1 / 2) m v^{2} - (1 / 2) 2 m {(v / 2)}^{2} = m v^{2} / 4

. Ezt tesszük egyenlővé a legkisebb energiaadaggal:

\begin{matrix} \frac{m v^{2}}{4} = Δ E; \end{matrix}

innen

v = \sqrt[]{4 \cdot Δ E / m} = 6, 26 \cdot 10^{4} m/s

.
A rugalmatlan ütközés utáni közös sebesség

v / 2 = 3, 13 \cdot 10^{4} m/s

.
A második kérdés a Doppler-jelenséggel áll kapcsolatban. A fénysebességhez képest ilyen kis sebességek esetében jó közelítéssel a relatív sebességarány adja meg a relatív frekvenciaváltozást. A relatív sebességarány:

\begin{matrix} 6, 26 \cdot 10^{4} : 3 \cdot 10^{8} = 2, 09 \cdot 10^{- 4} = 2, 09 \cdot 10^{- 2} % . \end{matrix}

Az egyik fénysugárnál ennyivel több, a másiknál ennyivel kevesebb az észlelt fény rezgésszáma. A kibocsátott fény egyébként az ultraibolya Lyman-sorozat leghosszabb,

0, 1216 μ m

hullámhosszúságú vonala.

II. feladat. Adott egy

d

vastagságú lemez, amelynek a törésmutatója az

x

tengely irányában a következő képlet szerint változik (1. ábra):

\begin{matrix} n = \frac{n_{0}}{1 - x / r} . \end{matrix}

O

pontban a lemezre merőlegesen egy fénysugarat ejtünk be a levegőből és ez a lemezt egy bizonyos

A

pontban,

α

kilépési szöggel hagyja el. Mekkora az

n_{A}

törésmutató az

A

pontban? Hol van az

A

pont? Milyen vastag a lemez? Számadataink:

n_{0} = 1, 2

r = 13 cm

α = 30^{\circ}

1. ábra

Megoldás. Talán a legjobb, ha a legizgatóbb kérdés elintézésével kezdjük: milyen a fénysugár pályájának az alakja? Ha egymás után állított planparalel lemezeken megy át a fény (2. ábra), amelyek törésmutatója fokozatosan változik, akkor az egyes törésekre felírt töréstörvény szerint: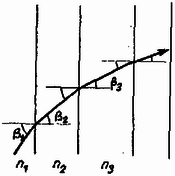

\begin{matrix} \frac{sin β_{1}}{sin β_{2}} = \frac{n_{2}}{n_{1}}, \frac{sin β_{2}}{sin β_{3}} = \frac{n_{3}}{n_{2}}, ..., \end{matrix}

illetve

\begin{matrix} n_{1} sin β = n_{2} sin β_{2}, n_{2} sin β_{2} = n_{3} sin β_{3}, ... \end{matrix}

2. ábra

Ez az összefüggés akármilyen vékony rétegekből álló sorozat esetében is igaz, ezért minden olyan esetben, ha a törésmutató csak az

x

tengely mentén változik:

\begin{matrix} n_{x} sin β_{x} = konstans . \end{matrix}

A mi esetünkben a fény

n_{0}

törésmutatójú helyen alulról merőlegesen lép a lemezbe, amikor is

n_{x} = n_{0}

és

β_{x} = 90^{\circ}

, tehát nálunk a konstans

n_{0}

és bárhol a lemezben:

\begin{matrix} n_{x} sin β_{x} = n_{0} . \end{matrix}

Azonban ismerjük

n_{x}

függését

x

-től és így a lemez belsejében a fénysugár mentén igaz, hogy (3. ábra):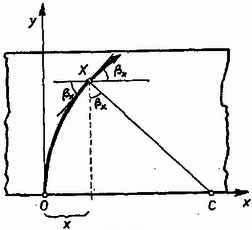

\begin{matrix} sin β_{x} = \frac{n_{0}}{n_{x}} = 1 - \frac{x}{r} = \frac{r - x}{r} . \end{matrix}

3. ábra

Rajzoljunk a kérdéses pontban a fénysugár érintőjére merőlegest. Az ábrát egybevetve a fizikai levezetésből származó eredménnyel, azonnal látszik, hogy a fénypálya egy körív, amelynek rádiusza

O C = X C = r

, éppen az alapképletben szereplő konstans és középpontja

C

. Pontosabban: erre a körívre nyilván teljesül a

sin β_{x} = (r - x) / r

összefüggés; azt pedig, hogy más görbe nem felel meg, annak alapján láthatjuk be, hogy az adott

O

ponton áthaladó görbe deriváltja, azaz érintőjének iránytangense adott:

tg β_{x} = sin β_{x} / \sqrt[]{1 - sin^{2} β_{x}}

. Ez igen érdekes eredmény, amit legfeljebb abból lehetett előre sejteni, hogy a konstans jelölése

r

volt.
Sorban válaszolunk a kérdésekre. Az

A

pontban, tekintettel a levegőbe való kilépésre, a fénytörés törvénye szerint

\begin{matrix} \frac{sin α}{sin (90^{\circ} - β_{A})} = n_{A} = \frac{sin α}{cos β_{A}} . \end{matrix}

Azonban az

n_{A} sin β_{A} = n_{0}

szerint

sin β_{A} = n_{0} / n_{A}

cos β_{A} = \sqrt[]{1 - {(n_{0} / n_{A})}^{2}}

, és ezt felhasználva:

\begin{matrix} n_{A} = \frac{sin α}{\sqrt[]{1 - {(n_{0} / n_{A})}^{2}}} . \end{matrix}

Innen

n_{A} = \sqrt[]{n_{0}^{2} + sin^{2} α}

; az

n_{0} = 1, 2

és

sin α = 0, 5

értékek felhasználásával

n_{A} = 1, 3

. Az

A

pont

x

koordinátája az

1, 3 = 1, 2 / (1 - x / 13)

kiindulási képletből

x = 1 cm

.
A falvastagság kiszámításánál figyelembe vesszük, hogy a kör alakú fénypálya egyenlete

y^{2} + {(r - x)}^{2} = r^{2}

x = 1 cm

és

r = 13 cm

, így

d = y = 5 cm

.
Felvethető az a gondolat, mi történik, ha adott üveglapunkba nem az

1, 2

-es törésmutatójú helyen, hanem odébb, balra vagy jobbra engedjük be merőlegesen a fénysugarat (4. ábra).

4. ábra

O

-ban beejtett fénysugár legfeljebb negyedkört írhat le, mert

O C = r = 13 cm

távolságban a törésmutató végtelen lesz. Az előbbihez hasonló gondolatmenetből következik, hogy valamennyi fénysugár koncentrikus negyedkörön futna, így egy véges vastagságú fénysugár szépen elkanyarodna. De a beejtés pontját nem szabad

O

-tól balra messzebbre, mint

2, 6 cm

-re vinni, mert ott a törésmutató

1

lesz.
Egy másik gondolat. Az ember először azt hiszi, hogy az alulról merőlegesen beejtett sugárnak irányváltozás nélkül kellene továbbhaladnia, hiszen a merőleges vonal mentén a törésmutató mindenütt ugyanannyi (5. ábra).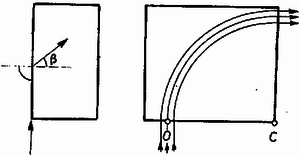

5. ábra

Ugyanolyan határesetről van szó, mint amikor egy üvegtömbre súrlódva ejtünk be egy fénysugarat, amelynek azután a törvény szerint

sin β = 1 / n

törőszöggel kellene továbbmennie. Egyetlen homogén üvegtömbnél ez a határeset gyakorlatilag kivihetetlen, de a mi lemezünknél alkalmazhatunk véges vastagságú nyalábot és az ilyen kísérlet el volna végezhető.

Meszéna Géza

III. feladat. Egy tudományos expedíció magányos szigetre vetődik, minden energiaforrás nélkül. Szélcsend van, a tenger nem hullámzik, mindenütt ugyanannyi a hőmérséklet és a légnyomás. Tudósaink végszükségben felfedeznek egy gázforrást, amelyben kémiailag indifferens, levegőnél nehezebb gáz van a légkörivel egyező nyomáson és hőmérsékleten. Az expedíció rendelkezik két membránnal, közülük az egyik csak a gázt, a másik csak levegőt enged át. Készíthetnek-e ezekkel munkát végző gépet és hogyan? Mennyi munkát kaphatnak eszközükkel?

Megoldás. A következő fizikai törvényeket kell ismerni. Ha egy tartályban többféle gáz van, akkor parciális nyomásnak azt a nyomást nevezzük, amelyet a gáz akkor fejtene ki, ha egyedül volna jelen a tartályban. A gázkeverék tartályára kapcsolt nyomásmérő ezeknek a parciális nyomásoknak az összegét mutatja. Ha egy membrán valamely gázra nézve átjárható, akkor ennek a gáznak a membrán mindkét oldalán ugyanannyi lesz a parciális nyomása.
A 6. ábra mutat egy ilyen gépet. A dugattyú alatt mindig

1

atmoszféra a levegő parciális nyomása, tekintettel a henger alján levő szűrőre. Tehát munkavégzés szempontjából nem kell foglalkoznunk a légköri levegő nyomásával. A gáz viszont nem tud megszökni a hengerből.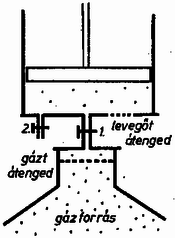

6. ábra

Kinyitjuk az 1. szelepet, melynek vezetékében van a gázt átengedő membrán. Ennek mindkét oldalán

1

atmoszféra lesz a gáz parciális nyomása, így a hengerben a dugattyú alatt is. A dugattyú alatt az összes nyomás

2

atmoszféra, fölötte csak

1

, ezért a dugattyú felfelé megy és munkát végez. Egy idő múlva lezárjuk az 1. szelepet. A dugattyú tovább megy felfelé, a bezárt gáz parciális nyomása közben a Boyle ‐ Mariotte-törvény szerint közeledik a nullához, illetőleg az összes nyomás az

1

atmoszférához. Feltételeztük, hogy a henger fala jó hővezető anyagból készült, és a dugattyút elég lassan engedjük mozogni ahhoz, hogy a hőmérséklet mindig kiegyenlítődjék.

1 mól T

hőmérsékletű gáz térfogatának

V_{1}

-ről

V_{2}

-re való izotermikus növelése közben

R T ln (V_{2} / V_{1})

munkát végez, azaz mivel

V_{2}

nagyságát semmi sem korlátozza, tetszőleges

V_{1}

eredeti térfogatú gázból is végtelen mennyiségű energiát nyerhetünk. (Természetesen más feltételekkel is kiszámíthattuk volna az energianyereséget ‐ pl. adiabatikus tágulást feltételezve ‐, az eredmény akkor is végtelen.) (L. a KML 1969. évi 3. szám 129. oldalát.)
Ha a dugattyú felfelé tartó menetét abba kell hagynunk, az 1. szelepet bezárjuk és kinyitjuk a 2. szelepet, erre teljes külső-belső nyomásegyenlőség jön létre, a dugattyú visszaesik, illetve munka nélkül visszatolható. Újabb gázadaggal az eljárás megismételhető.
A munkavégzés készülékünknél a környezet lehűlésével jár együtt. A dugattyú felfelé menetelekor teljes egészében munkavégzésként kaptuk meg a környezetből felvett hőt. A termodinamika II. főtételében szereplő hatásfokkal nem kell foglalkoznunk, mert itt szó sincs körfoyamatról: a gáz egyes adagjai irreverzibilisen szétkeverednek a légkörben.
A két membránnal ugyanazt az állapotot értük el, mintha csak a gázforrás létezett volna, de légkör nélkül, vákuumban.

Kísérleti feladat. Az adott lezárt dobozban két egyforma félvezető dióda és egy ohmikus ellenállás van, valamilyen kapcsolásban. Megállapítandó az ellenállás nagysága.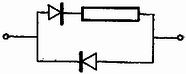

Megoldás. Két különböző feszültséggel kétféle irányban mérve áramerősséget a következők derülnek ki: mindkét irányban van áramvezetés, de különböző mértékben, és az áramerősség egyik esetben sem lineáris függvénye a feszültségnek. Ebből szükségképp következik a 7. ábrán látható kapcsolás.

7. ábra

Ezután fel kell venni mindkét irányban a pontos feszültség‐áramerősség karakterisztikát. Ha két irányban ugyanakkora abszolút értékű áramot vezetünk át, akkor az ezekhez tartozó feszültségkülönbség az ellenállásra jutó feszültséget adja meg. Ezt osztva az áramerősséggel, kapjuk az ellenállás nagyságát.