Cím: 1974. évi fizika OKTV feladatai
Füzet: 1974/október, 83 - 89. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1974. évi középiskolai tanulmányi verseny feladatai
 

Az I. forduló feladatai
 

1. A Föld körül keringő úrhajóban hogyan tudná valamely test tömegét (tehetetlenségének mértékét) meghatározni? A meghajtórakéták már nem működnek, a levegő ellenállása elhanyagolható. Adjunk meg minél többféle eljárást: ismertessük a szükséges összefüggéseket és eszközöket! Ezek közül melyeket kellett előzőleg hitelesíteni?
(Párkányi László)
 

Megoldás. A lehetséges eljárások közül kézenfekvő vagy az erőtörvény, vagy az impulzusmegmaradás törvényének alkalmazása. Az F=ma erőtörvény alkalmazásra kerülhet például mint gyorsulásmérés, mint a centripetális erő mérése vagy mint rugó rezgés idejének mérése stb. Mindegyik esetben szükség van hitelesített méterrúdra, órára és erőmérőre. Amennyiben hitelesített tömegetalont használunk, kevesebb hitelesített mérőeszközzel is beérhetjük. Az impulzustörvényt alkalmazhatjuk úgy, hogy egy rugó dob szét két tömeget, vagy mint ütközést. Hitélesített tömegetalonon kívül távolságarányt megállapító hosszmérő eszközre is szükségünk van.
 

2. Az m1=8kg-os és m2=17kg-os kocsik csigán átvetett fonállal összekapcsolva mozognak (1. ábra). Az m2 tömegű kocsi α=36∘52'-es lejtón van. A súrlódás elhanyagolható. Hogyan helyezkedik el mozgás közben az m1 és az m2 tömegű kacsiban lógó inga?
(Vermes Miklós)
 

 

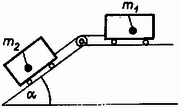1. ábra
 

Megoldás. Először a kocsik közös gyorsulását kell kiszámítanunk az erőtörvény alapján:
a=Fm=m2gsinαm1+m2.

Az inga fonalában ható feszítőerő és az inga tömegére ható súlyerő eredője adja az inga tömegét gyorsító ma erőt. Az m1 tömegű kocsiban lógó inga esetében (2. ábra):
tgφ1=ag=m2sinαm1+m2.
 

 

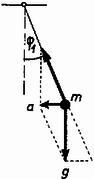2. ábra
 

Az m2 tömegű kacsiban lógó inga esetében írjuk fel az erők összetevőit (3. ábra). F a fonálban ható erőt jelenti.
 

 

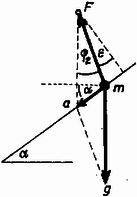3. ábra
 
 

Vízszintesen:  macosα=Fsinφ2,
Függőlegesen:  masinα=mg-Fcosφ2.
 


F kiküszöbölésével φ2-re kapjuk:
tgφ2=acosαg-asinα,
azután a kiszámított értékét felhasználva:
tgφ2=m2sinαcosαm1+m2cos2α.
Ha a kocsi merőlegesével alkotott ε szöget nézzük, akkor ε=α-φ2, ezért:
tgε=m1tg αm1+m2.

A mi számadatainkkal a=51g/125=4m/s2, tg φ1=51/125=0,408, φ1=22∘ 12', tg φ2=51/118=0,4322, φ2=23∘22',tg ε=6/25=0,24, ε=13∘ 30'.
 

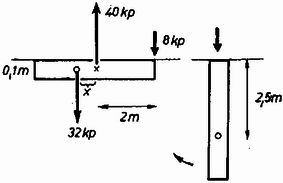
3. Az 1dm2 alapterületű, 4 méter hosszú, fából készült négyzetes oszlop függőlegesen úszik egy tóban, mert súlypontja nincs a közepén (4. ábra). Ahhoz, hogy az oszlop vízszintes helyzetben éppen elmerülve ússzék, a rúd végét F=8kp erővel kell függőlegesen lefelé nyomni. Hol van az oszlop súlypontja? Mennyi munka árán hoztuk az oszlopot ebbe a helyzetbe?
(Wiedemann László)
 

 

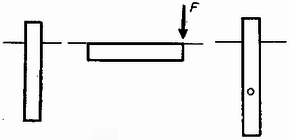4. ábra
 

Megoldás. Az oszlop térfogata 40dm3; miivel 8 kp hatására merül éppen be, és a felhajtóerő 40 kp, azért saját súlya 32 kp. Függőleges helyzetben 8 dm áll ki a vízből, hiszen ekkor lesz a felhajtóerő 32 kp.
Jelölje x a súlypont távolságát a középtől (5. ábra).
 

 

5. ábra
 

A vízszintes helyzetben az emelőtörvény szerint 32x=8⋅20, tehát x=5 dm. A súlypont a gerenda alsó végétől 15 dm-re, felső végétől 25 dm-re van.
A munka kiszámítása két lépésben történhet. Először függőleges helyzetében nyomjuk le az oszlopot. A megtett út 0,8 m. Közben az erő lineárisan növekszik 0-tól 8 kp-ig, tehát átlagosan 4 kp erővel kell számolnunk. Így a munkavégzésnek ez a része 4⋅0,8mkp=3,2 kp. Ezután emeljük fel az oszlopot a vízszintes helyzetbe. Az oszlop súlypontjának emelkedése 2,5m-0,05 m=2,45 m, a súly 32 kp, tehát 32⋅2,45mkp=78,4 mkp munkát kell végeznünk. Azonban 40 kp súlyú víz 2m-0,05 m=1,95 m mélységbe kerül le, ami 40⋅1,95mkp=78 mkp munkát ad. Tehát a második lépésben a munkavégzésünk 78,4mkp-78 mkp=0,4 mkp.
Az egész munkavégzés 3,2mkp+0,4 mkp=3,6 mkp.
 
Megjegyzések. 1. A vízszintesen fekvő gerenda egyensúlyi helyzete labilis: a legkisebb zavar következtében lemegy a függőleges helyzetbe, miközben 8 kp erővel felső végét változatlanul a víz színén tartjuk.
2. Ha egy gerendát a végére kifejtett erővel vízszintes úszási helyzetbe kényszerítünk, akkor egyáltalán nem biztos, hogy teteje a víz felszínével egy szinten van. A mi gerendánk azonban megfelel ennek a speciális feltételnek.
 

A II. forduló feladatai
 

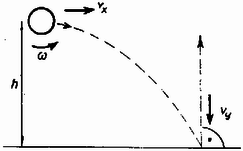
1. Az m=3 gramm tömegű pingponglabdát az asztal felett h=20 cm magasságban úgy ütöttük vissza, hogy kezdősebessége vízszintes lett. A labdát ,,megcsavartuk'', ezért a kezdősebességére merőleges vízszintes tengely kőrül forgásba is jött. Az asztalba való ütközése után, onnan már forgás nélkül, pontosan függőleges irányban pattant vissza (6. ábra). Legfeljebb mekkora hőmennyiség keletkezhet az asztalba ütközés folyamán, ha az ütközés rugalmas, de a felület érdessége folytán a labda és az asztal között μ=0,25 a csúszási súrlódási együttható? g=10m/s2.
(Bodó Zalán)

 

 

6. ábra
 

Megoldás. Ha az indulási, vízszintes sebesség vx, és a szögsebesség ω, akkor a mechanikai energiaveszteség:
E=mvx22+Θω22,
mert megszűnt a vízszintes irányú haladó mozgás és a forgás. (Θ a labda tehetetlenségi nyomatéka.) Az asztalba ütközés függőleges sebességösszetevője az esés végsebességéből ismeretes:
vy=2gh.
A kezdeti vx sebességet és ω szögsebességet abból számíthatjuk ki, hogy mindkettőnek nullára, kell lefékeződnie. A Δt ideig tartó függőleges összenyomódás alatt működő függőleges erő az impulzusváltozásból:
F=2mvyΔt.(1)
A kerület mentén fékező súrlódási erő:
Fs=μF=2μmvyΔt.(2)

Ha a haladó mozgás lefékeződése Δτ ideig tart, akkor a vízszintes irányú impulzusváltozás:
mvx=μFΔτ=2μmvyΔt⋅Δτ.
Ha Δt=Δτ, akkor mvx=2μmvy és az indulási vízszintes sebesség nagysága:
vx=2μvy.(3)

A forgás ugyancsak Δτ idő alatt fékeződött le ω-ról 0-ra, tehát a szöggyorsulás β=ωΔτ. A forgás alaptörvénye szerint a forgatónyomatékot a tehetetlenségi nyomaték és a szöggyorsulás szorzata adja meg:
Fsr=Θ⋅ωΔτ,
amiből ismeretessé válik a kezdeti szögsebesség:
ω=FsrΘ⋅Δτ.
Az erő (1), illetve (2) szerinti értékeivel:
ω=2μmvyrΔt⋅Θ⋅Δτ.
Ismét a Δt=Δτ feltétel alapján kapjuk, hogy a kezdeti szögsebesség:
ω=2μmvyrΘ.(4)

(3) és (4) ismeretében számítható a mechanikai energiaveszteség:
E=mvx22+Θω32=2mμ2vy2+2m2μ2vy2r2Θ.
Mivel vy2=2gh, továbbá, labda esetében Θ=2mr2/3, az energiaveszteség:
E=μ2mgh+6μ2mgh=10μ2mgh.(5)
Számadatainkkal vy=2m/s,vx=1m/s,ω=150s-1,E=3,75⋅10-3joule=0,893⋅10-3 cal.
Azonban eredményünk csak az energiaveszteség lehetséges felső határát adja meg. Lehetséges, hogy a vízszintes impulzusösszetevő és a szögsebesség előbb szűnt meg, mint a benyomódás, vagyis Δτ<Δt. Ekkor vx és ω is kisebb a (3) és (4) által megadott értékeknél, a vízszintes sebesség és szögsebesség az induláskor kevesebb volt, mint amit számítottunk, így a mozgási energia vesztesége szintén kevesebb, mint amit az (5) alatti eredmény ad meg.
 

2. Egy csillagászati távcső tárgylencséje na=2,5, szemlencséje nb=1,5 törésmutatójú anyagból készült. Ha a távcsövet megtöltjük egy folyadékkal és ebbe a folyadékba mártva használjuk, akkor végtelenre való élesre állítása és nagyítása (pontosan: a szögnagyítás abszolút értéke) változatlan marad. Mennyi ennek a folyadéknak a törésmutatója? Mekkora a nagyítás?
(Bodó Zalán)
 

Megoldás. Levegőben a tárgylencse, illetőleg szemlencse fókusztávolsága:
1fa=(na-1)⋅K,1fb=(nb-1)⋅L.
Itt a lencsék rádiuszait tartalmazó rövidítések:
K=1R1+1R2,L=1RI+1RII.

Az n törésmutatójú folyadékba való mártáskor a fókusztávolságok:
1Fa=na-nn⋅K,1Fb=nb-nn⋅L.
A nagyítás a levegőben, illetve a folyadékban:
fafb=nb-1na-1⋅LK,FaFb=nb-nna-n⋅LK.

Írjuk fel a nagyítások egyenlőségét:
nb-1na-1=nb-nna-n.
Ennek az egyenletnek a megoldása n=1, vagyis a levegőben használt távcső. De ha az egyik távcső Kepler-féle, a másik Galilei-féle, akkor az egyenlet:
nb-1na-1=-nb-nna-n.
Ennek az egyenletnek a megoldása:
n=2nanb-na-nbna+nb-2=1,75.

Számítsuk a nagyítást. A távcső változatlan hossza folytán:
fa+fb=Fa+Fb;
felhasználva a fókusztávolságok értékeit:
1(na-1)K+1(nb-1)L=n(na-n)K+n(nb-n)L,
aminek rendezéséből egy feltétel adódik a lencsék geometriai adataira vonatkozóan:
LK=-nb(na-n)(na-1)na(nb-n)(nb-1).
Ezt felhasználva a táveső nagyításánál:
fafb=nb-1na-1⋅LK=nb(na-n)na(n-nb).
Az n-re kapott eredményünket ide helyettesítve:
fafb=nb(na-1)na(nb-1)=95,
illetve
FaFb=-95,
 

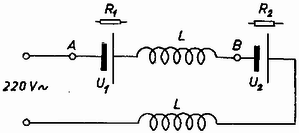
3. A 7. ábra szerint 220 voltos hálózati feszültségre kapcsoltunk két egyenlő önindukciója tekercset és két galvántelepet, amelyeknek elektromotoros ereje U1=50 volt, illetve U2=100 volt és belső ellenállásuk nem elhanyagolható. A váltakozó áram erőssége a feszültséghez képest 45∘ -os fáziskésésben van. Az A és B pontokra kapcsolt egyenáramú feszültségmérő nem mutat feszültséget. Mennyit mutat az A és B pontokra kapcsolt váltakozó áramú feszültségmérő?
(Wiedemann László)

 

 

7. ábra
 

Megoldás. Egyenáramú voltmérő esetében a helyzet olyan, mintha az áramkörben csak a galvántelepek adnának feszültséget,a 220 voltos váltakozó áramú feszültségforrás rövidre volna zárva és az önindukcióknak sincs szerepük. Ekkor
U1=iR1,U1+U2=i(R1+R2);
innen R2=2R1.
A váltakozó áramnál a. 45∘-os fáziskésés miatt 2ωL=R1+R2, így R1=2ωL/3,R2=4ωL/3.

Az eredő impedancia:
Z=(R1+R2)2+(2ωL)2=22ωL.
Az áramerősség:
I=UZ=U22ωL.
Az A és B pontok között az impedancia:
Z1=R12+(ωL)2=49(ωL)2+(ωL)2=133⋅ωL,
az erre jutó feszültség:
U=IZ1=U22ωL⋅133⋅ωL=2612⋅U=0,425U=93,5volt.  

 

III. (kísérleti) forduló
 

A II. forduló dolgozatai alapján 19 versenyző kísérletező versenyen vett részt Budapesten az ELTE Természettudományi Karának Általános Fizikai Tanszékén. Három feladattal foglalkoztak: megfelelő eszközzel igazolni kellett a fizikai inga lengésidőképletét, elemezni kellett egy elektromos kapcsolást és váltakozó áramú ellenállást kellett mérni.
 
Az 1974. évi fizikai tanulmányi verseny eredménye:
 

I, díj: Csuka Gábor (Budapest, Apáczai Csere Gimn. IV. o. t., tanára: Turtóczky Sándor).
II. díj: Pálfalvi György (Győr, Révai Miklós Gimn. TV. o. t., tanára: Székely László).
III. díj: Kertész Gábor (Budapest, 1. István-Gimn. IV. o. t., tanára: Cseh Géza).
A további helyezettek: 4. Vecsernyés Péter (Szeged, Radnóti Milós Gimn. IV. o. t., Maláj Györgyné), 5. Vladár Károly (Kiskunhalas, Szilády Áron Gimn. IV. o, t., Péter Irén), 6. Németh Tibor (Budapest, Berzsenyi Gimn. IV. o. t., Hubert Györgyné), 7. Simányi Nándor (Budapest, József Attila Gimn. TV. o. t., Ujj János), 8. Meszéna Géza (Budapest, Berzsenyi Gimn. TV. o. t., Apró Pál), 9. Keskeny András (Eger, Gárdonyi Géza Gimn. o. t., Bodnár István), 10. Szuhay Péter (Budapest, I. István Gimn. ÍV. o. t., Cseh Géza).