Kezdőlap


Cím:	1973. évi Eötvös Loránd Fizikaverseny
Füzet:	1974/február, 81. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat október 20-án rendezte ez évi, az 1916 óta tartott versenyek sorában ötvenedik versenyét Budapesten és 7 vidéki városban az idén érettségizettek és középiskolai tanulók számára. A versenyzők 5 óráig dolgozhattak és bármilyen segédeszközt használhattak. A versenyzők száma 329 volt. Ismertetjük a feladatokat és megoldásukat.

1. Súrlódásmentes, egyenes, vízszintes sínen két kocsi áll,

m_{2}

és

m_{3}

tömegekkel (1. ábra). Balról egy

m_{1}

tömegű kocsi érkezik tetszőleges

v_{1}

sebességgel. Legyen

m_{1} = 8 kg

m_{3} = 6 kg

. Elképzelhető-e olyan

m_{2}

tömeg, hogy az összes ütközés lezajlása után a középső kocsi újra éppen nyugalomba kerül? Valamennyi ütközés tökéletesen rugalmas.
(Károlyházy Frigyes)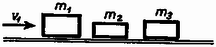

1. ábra

Megoldás. Ha az összes ütközés lezajlása után

m_{2}

nyugalomban marad, akkor kihagyható az impulzus- és energiamegmaradás egyenleteiből. A rugalmas ütközés utáni sebességek az impulzus és energia megmaradásán alapuló ismert képletek szerint:

\begin{matrix} u_{1} = 2 c - v_{1}, u_{3} = 2 c - v_{3}, \end{matrix}

ahol

c

a közös súlypont sebessége:

c = \frac{m_{1} v_{1} + m_{3} v_{3}}{m_{1} + m_{3}}

. Mivel most

v_{3} = 0

, a mi esetünkben az ütközés utáni sebességek:

\begin{matrix} u_{1} & = \frac{v_{1} (m_{1} - m_{3})}{m_{1} + m_{3}}, \\ u_{3} & = \frac{2 m_{1} v_{1}}{m_{1} + m_{3}} . \end{matrix}

A végén

m_{1}

sebessége negatív kell, hogy legyen, ennek feltétele:

m_{3} > m_{1}

. Ez adatainkra nem teljesül, tehát nem lehet megfelelő

m_{2}

tömeget találni.

2. Egyenlő oldalú hengerből és ugyanakkora magasságú, egyharmad átmérőjű hengerből álló edényt alul elhanyagolható térfogatú cső köt össze. A vékonyabb henger zárt, a vastag henger felül nyitott (2. ábra baloldali rajza). Az üres hengerbe addig töltünk higanyt, amíg a vastag henger négyötöd részig, a vékony henger háromtized részig telik meg. Hány

c m^{3}

higany van most az edényben? A légköri levegő nyomása

1033 {p/cm}^{2}

, a higany sűrűsége 13,6 g/cm

^{3}

.
(Lipták László)

Megoldás. Tekintsük először a hengerek

x

magasságát ismeretlennek. Felírjuk Boyle‐Mariotte törvényét a vékony hengerbe zárt levegőre: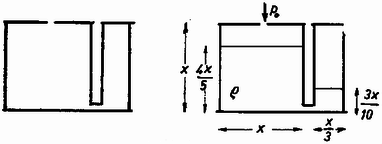

\begin{matrix} p_{0} x \cdot \frac{π}{4} {(\frac{x}{3})}^{2} = [p_{0} + (\frac{4 x}{5} - \frac{3 x}{10}) ϱ g] \cdot \frac{7 x}{10} \cdot \frac{π}{4} {(\frac{x}{3})}^{2} . \end{matrix}

2. ábra

Innen:

\begin{matrix} x = \frac{6 p_{0}}{7 ϱ g} = \frac{6 \cdot 1033 \cdot {p/cm}^{2}}{7 \cdot 13, 6 \cdot {g/cm}^{3} \cdot 9, 8 {m/s}^{2}} = \frac{6 \cdot 1033}{7 \cdot 13, 6 \cdot 9, 8} \cdot \frac{10^{- 3} \cdot 9, 8 \cdot kg \cdot {m/s}^{2} \cdot cm}{10^{- 3} \cdot kg \cdot {m/s}^{2}} = 65 cm . \end{matrix}

A higany térfogata:

\begin{matrix} \frac{4 x}{5} \cdot \frac{π}{4} \cdot x^{2} + \frac{3 x}{10} \cdot \frac{π}{4} \cdot {(\frac{x}{3})}^{2} = \frac{5 π}{24} \cdot x^{3} = 0, 654 x^{3} = 179 600 {cm}^{3} . \end{matrix}

A feladat szövegében először meglepő, hogy csupa relatív adatból kíván konkrét, méretes eredményt, de a numerikus adatok a nyomás és sűrűség értékeiben rejtőznek.

3. Adott

N

darab egyformán

E_{0}

elektromotoros erejű és

r_{0}

belső ellenállású galvánelem, valamint egy

R

ellenállás. Hogyan kapcsoljuk össze az elemeket, hogy a keletkező telep a lehető legnagyobb teljesítményt szolgáltassa az

R

ellenálláson? Mekkora lesz ez a teljesítmény? Vizsgáljuk meg a problémát a következő numerikus értékek mellett:

E_{0} = 1 volt

r_{0} = 1 ohm

R = 5 ohm

N_{1} = 4

, illetőleg

N_{2} = 100

.
(Radnai Gyula)

Megoldás. A 3. ábra mutatja 4 elem esetében az egyszerű elrendezéseket, amikor csak egyenlő elektromotoros erejű összeállítások kerülnek párhuzamosan egymás mellé.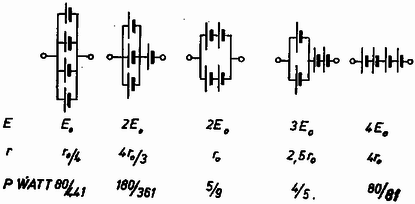

3. ábra

E

elektromotoros erő esetében,

r

belső ellenállás mellett az áramerősség

i = E / (r + R)

, a kapocsfeszültség

U = E R / (r + R)

, a teljesítmény:

\begin{matrix} P = E^{2} R \cdot \frac{1}{{(r + R)}^{2}} = \frac{E^{2} R}{r^{2}} \cdot \frac{1}{{(1 + R / r)}^{2}} . \end{matrix}

A 3. ábrán látható adatokból kitűnik, hogy a tisztán soros kapcsolás ebben az esetben a legkedvezőbb

80 / 81 = 0, 988

watt teljesítménnyel. Az egyenlő belső és külső ellenállású esethez tartozó maximum

E^{2} R / 4 r^{2} = 1, 25

watt volna.
100 elem esetében már célszerű valamilyen rendszer alapján elindulni.

4. ábra

Ha az elemeket téglalap alakjában rendezzük el

y

sorban és mindegyikben

x

elemmel (4. ábra), akkor az elektromotoros erő

E = x E_{0}

, a belső ellenállás

r = x r_{0} / y

, és a teljesítmény, felhasználva, hogy

x y = N

\begin{matrix} P = \frac{x^{2} E_{0}^{2} R}{x^{2} r_{0}^{2} / y^{2}} \cdot \frac{1}{{[1 + y R / (x r_{0})]}^{2}} = \frac{E_{0}^{2} R}{r_{0}^{2}} \cdot \frac{N^{2}}{{[x + N R / (r_{0} x)]}^{2}} . \end{matrix}

Ennek a függvénynek ott van maximuma, ahol a nevezőben levő négyzetalapnak minimuma van. Ez akkor következik be, ha

\begin{matrix} x = \sqrt[]{\frac{N R}{r_{0}}}; \end{matrix}

ebben az esetben

y = \sqrt[]{N r_{0} / R}

, az egész telep belső ellenállása

r = R

, és a teljesítmény

P = E_{0}^{2} N / 4 r_{0}

N = 100

esetében

x = \sqrt[]{500} = 24, 2

y = \sqrt[]{20} = 4, 84

és

P = 25

watt volna. Minimum‐esetünket egészszámos összeállítással kell megközelítenünk. Ilyeneket mutat táblázatunk:

\begin{matrix} x & y & rohm & Pwatt \\ 10 & 10 & 1 & 125 / 9 = 13, 889 \\ 20 & 5 & 4 & 2000 / 81 = 24, 691 \\ 25 & 4 & 6, 25 & 2000 / 81 = 24, 691 \\ 50 & 2 & 25 & 125 / 9 = 13, 998 \end{matrix}

P

függvény

x = \sqrt[]{N R / r_{0}}

-ig nő, azután csökken és elég lapos maximumot mutat. Táblázatunk két középső sora jelenti a maximális teljesítményt.
Érdekes, hogy ha nem téglalapos elrendezéssel (például 15 elem 5 sorban párhuzamosan, azután ezekkel

4 \cdot 4

és

3 \cdot 3

sorban) kierőszakoljuk a pontosan 5 ohmos belső ellenállást, akkor a teljesítmény csak

125 / 5 = 24, 2

watt. A vegyes téglalapos és különböző elektromotoros erejű részeket párhuzamosan tartalmazó kapcsolásokat nehéz áttekinteni, ezek között eddig még nem sikerült olyat találni, amelynek a teljesítménye elérte volna a 2000/81 wattot.

A verseny eredménye. Az 1973. évi Eötvös‐verseny összevont díjait egyenlő arányban megosztva kapták Kertész Gábor, a budapesti I. István Gimnázium IV. osztályában Cseh Géza tanítványa, Koltai Ferenc honvéd (a budapesti I. István Gimnáziumban érettségizett mint Moór Ágnes tanítványa), Meszéna Géza, a budapesti Berzsenyi Gimnázium IV. osztályában Apró Pál tanítványa és Simányi Nándor, a budapesti József Attila Gimnázium IV. osztályában Ujj János tanítványa. Dicséretet kaptak könyvjutalommal Nuspl János honvéd (a bajai III. Béla Gimnáziumban érettségizett mint Pécsi József tanítványa), Prőhle Péter, a budapesti Fazekas Gimnázium IV. osztályában Szücs Barna tanítványa és Vojtilla László, a miskolci Nehézipari Műszaki Egyetem hallgatója (a miskolci Földes Ferenc Gimnáziumban érettségizett mint Polák Gabriella tanítványa).