Cím: A téridő
Szerző(k):  Vermes Miklós 
Füzet: 1973/december, 225 - 228. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ember így szokott beszélni: ez a vagon 20 méter hosszú, a tanítási óra 45 percig tart stb. Mert ha a pályaudvar sínén álló vagon elejét és végét megjelöljük a földön, akkor erre a távolságra a méterrudat 20-szor lehet ráfektetni, illetve a becsengetéskor megindított stopperóra mutatója kicsengetéskor a 45-ös percnél áll. Talán reprodukálhatóbb időpélda: a 84-pólonium-218 (rádium A) radioaktív izotóp felezési ideje óránk szerint 3 perc. Megszoktuk, hogy ezek az adatok a vagonra, a radioaktív elemre állandó, változatlan jellemző számok. A folyóiratunkban megjelent két cikk alapján (l a szeptemberi és a novemberi számot) tudjuk, hogy a nagy sebességek esetében ez nincs így. Ha a vonat képes volna 0,6c=180000 km/s sebességgel haladni, akkor megjelölve a töltésen mozgó vagon elejének és végének egyidejű helyeit, ezek távolságát 0,8⋅21=16 méternek találnánk, és ha a vonaton utazó tudós jelezné például az ablakból egy-egy intéssel a felezés elejét és végét, akkor ezt az időközt a töltés mellett álló megfigyelők 3/0,8=3,75 percnek találnák. Ha a vonat nem is, de elemi részecskék repülnek olykor a fényt megközelítő sebességgel, és ilyenkor a tapasztalat tényleg mutatja ezt a jelenséget.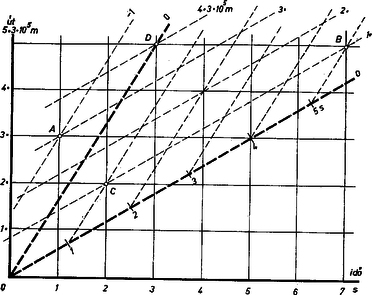
Tehát a mozgó szerkezet, rendszer hossz- és időadatai az állóból mérve függenek a sebességtől. Egy néhány példán tanulmányozzuk ezeket a dolgokat. Ábránk azonos a legutóbbi cikk 3. ábrájával.

 

 

Az úttengely mentén v=0,6c sebességgel mozgó tárgyak idő- és távolságkoordinátáit az álló rendszerben a derékszögű, folytonos vonalak sorszámától, a mozgó rendszerben a ferde szaggatott vonalak segítségével állapíthatjuk meg. Három példát vizsgálunk.
I. Az egyenesünk mentén 3⋅3⋅105 méternél áll az első megfigyelő és órája szerint 1 s-kor (A-pont) egy rakétát lőtt ki, a vonal mentén előre irányítva, és ez a rakéta az 5⋅3⋅105 méternél álló barátját érte el (B-pont) 7 s-kor. A rakétában küldött levél felszólította a B embert, hogy igyék barátja egészségére, és ez meg is történt. Egyébként a rakéta sebessége 2⋅3⋅105/6=105 m/s volt, ami a fénysebesség egyharmada és elvben nem lehetetlen. Ugyanezt az eseménysorozatot megfigyelte az egyenes pálya fölött 0,6c sebességgel repülő pilóta is. Azt látta, hogy -1 s-kor 3⋅3⋅105 méternél egy ember akinek a sapkáján A betű volt, egy rakétát indított el, és ez +5 s-kor ért el az 1⋅3⋅105 méternél álló B emberhez, aki a levelet elolvasva nagyott húzott a kulacsából. A repülő az események időközét 6 s-nak, az emberek távolságát 2⋅3⋅105 méternek észlelte, de úgy, hogy A van elől és B hátul, a rakéta a repülőgép haladási irányával ellentétesen repült. Nem csoda, hiszen sebessége kevesebb volt. A repülő más időközt észlelt, mint az emberek és számára megfordult a térbeli helyzet. De a pilóta is úgy látta, hogy a levelet A küldte és ennek következtében kortyintott B.
II. Egyenes utunk mentén 2⋅3⋅105 méternél áll C barátunk és 2 s-kor tüsszent egy nagyot (C-pont). Másik barátunk, D az 5⋅3⋅105 méteres helyen áll és 3 s-kor cigarettára gyújt (D pont). Mit látott az egyenes út felett repülő pilóta? Egy C jelű ember 1⋅3⋅105 méternél állva 1 s tüsszentett. D Pedig 4⋅3⋅105 méternél 0 s-kor gyújtott cigarettára. Számára a távolság változatlanul 3⋅3⋅105 méter maradt, az időköz abszolút nagysága sem változott, 1 másodperc maradt, de az idősorrend megfordult! A repülő számára előbb gyújtott D cigarettára és azután tüsszentett C. Lehetséges ez? Természetesen. De a két esemény nem lehetett okozati kapcsolatban, mert az álló rendszerben 3⋅3⋅105m/1s=3c, háromszoros fénysebességgel kellett volna a C tüsszentését jelentő hírnek D-hez eljutnia, hogy D reagálhasson rá, például egy jókívánsággal. Ilyen sebesség nincs. D Nem szerezhetett tudomást C tettéről, tiszta véletlen, hogy akkor cigarettára gyújtott. Ebből látható, hogy az idősorrend megfordulhat ugyan, de csak egymástól független eseményeknél, az ok és az okozat nem cserélhető fel.
III. C-emberünk 2⋅3⋅105 méternél képtelefon előtt ül és 2 s-kor tüsszent. Barátja B 5⋅3⋅105 méternél a képernyő előtt ül és 7 s-kor azt mondja: egészségedre! A hír átvivésének akadálya, 3⋅3⋅105m/5s=0,6c átviteli sebesség szükséges hozzá, ami lehetséges. Tehát 3⋅3⋅105 méteres utat a hír 5 s alatt teszi meg. Ezt az eseményt vizsgálja a pilóta. És mit lát? Szerinte C és B egymás mellett állnak 1⋅3⋅105 méternél, és az esemény időtartama 5-1=4 s. A pilóta számára távolság nincs, csak időköz.
Amint látjuk, nagy sebességek esetében sok minden lehetséges, ami a mindennapi életünkben szokatlan. Hosszúság, időtartam, egyidejűség, idősorrend, térbeli sorrend viszonylagosak. Már régebben is megtörtént, hogy finomabb észlelések változónak mutattak olyasmit, amit állandónak képzeltünk. Pl a vas sűrűsége melegen kisebb stb. A mostani helyzet sokkal meglepőbb és nyugtalanítóbb, hiszen olyan alapfogalmakat, mint tér és idő eddig abszolútnak képzeltünk el. Épp a fizika alapvető fogalmai bizonyultak relatívnak. Azonban a folytatás megnyugtató és gyönyörű.
Minkowski, a kiváló matematikus 1908-ban egy érdekes, a relativitás elméletben rejtőzködő kapcsolatot fedezett fel. Egy síkon x1, y1 és x2, y2 derékszögű koordinátákkal adott pontok távolságát a Pythagoras-tétellel számíthatjuk ki:
h2=(x2-x1)2+(y2-y1)2.
Az egyes pontok koordinátái a legkülönbözőbbek lehetnek a koordináta-rendszer elhelyezése szerint, de a h távolság mindig ugyanannyi, ahogyan mondani szokták: invariáns. A mechanikában egy pontszerű esemény koordinátái az egyenes mentén az s távolság és t az időpont. Minkowski t helyett a w=-1⋅c⋅t=ict mennyiséget választotta, ami szintén távolságjellegű. Most már s-sel és w-vel mint távolságokkal lehet számolni. II. példánk esetében C tüsszentésének koordinátái az álló rendszerben s1=2⋅3⋅105 m, w1=i⋅3⋅105⋅2 m; D cigarettára gyújtásának koordinátái S2-5⋅3⋅105 m, w2=i⋅3⋅105⋅3 m. A közönséges távolságmérési eljárás szerint járunk el:
I2=(s2-s1)2+(w2-w1)2,I2=(5-2)2⋅(3⋅105m)2-(3-2)2⋅(3⋅105m)2=(9-1)⋅(3⋅105m)2==8⋅(3⋅105m)2,I=8⋅3⋅105m.
Végezzük el ezt a számítást a mozgó repülőgép koordináta - rendszerében is. Itt S1=1⋅3⋅105 m, W1=i⋅3⋅105⋅1 m; S2=4⋅3⋅105 m, W2=0 tehát:
I2=(S2-S1)2+(W2-W1)2==(4-1)2⋅(3⋅105m)2-(0-1)2⋅(3⋅105m)2=8⋅(3⋅105m)2I=8⋅3⋅105m.

Ugyanazt kaptuk. Általánosságban meg fogjuk mutatni, hogy ha a távolságszámítás mintájára a jelenség távolság- és időadataiból egy egyesített mennyiséget számolunk ki, ez nem függ a koordináta-rendszerek sebességétől, mindig ugyanannyi, invariáns. A távolságból és az időkből ilyen módon számított mennyiség neve: intervallum. Példánkban a tüsszentés és cigarettára gyújtás közötti intervallum 8⋅3⋅105 méter. Ez sem nem távolság, sem időtartam, hanem ez a kettő együtt. (Önkény, hogy méterben kaptuk, megfelelő átszámítással másodperc is lehetett volna.)
Természetesen egyetlen numerikus példa nem döntő. Az intervallum állandóságát bizonyítani kell. Az első esemény legyen az origóban, S1=0, W1=0, a másodikra nézve pedig S2=S, W2=W=icT. Az intervallum négyzete a mozgó rendszerben:
I2=S2+W2=S2-c2T2.
A Lorentz-transzformáció ismert képleteivel, amelyekkel az 1176. számú feladatlapban is találkozunk:
I2=(s-vt1-v2/c2)2-c2(t-vs/c21-v2/c2)2==(s-vt)2-c2(t-vs/c2)21-v2/c2=s2c2+c2v2t2-c2t2-v2s2c2-v2==s2(c2-v2)-c2t2(c2-v2)c2-v2=s2-c2t2=s2+(ict)2.


Ez pedig a v sebességtől függetlenül az álló rendszerben számított intervallum. A valóságban a három térbeli és egy időbeli koordináta négytagú négyzetösszeggel adja az intervallum négyzetét, ekkor az ábra rajzolása nehézkesebb.
Minkowski felfedezése igen nagy jelentőségű: összeolvasztja a teret és az időt. Ha a távolság és időtartam szintézisét jelentő intervallummal számolunk, akkor az eredmény független a megfigyelő sebességétől. Külön számolva csak távolsággal vagy csak idővel ezekre kisebb, nagyobb értékeket kaphatunk, az egyik alkalmas koordináta-rendszerről nézve el is tűnhet. Például a III. példánkban csak az idő maradt meg, a távolság 0 lett. Felcserélődhetnek a sorrendek is. Külön vizsgálva a teret és az időt mindig csak az igazi jelenség egy-egy nézetét, vetületét kapjuk aszerint, hogy hogyan történik a vetítés, de nem a teljeset. Egy hasonlat: ha a levegőben egy tojás lóg és két megfigyelő csak az árnyékát látja, de magát a tárgyat nem, akkor az egyik esetleg 10cm2 területű kört, a másik 15cm2 területű oválist észlelhet. Ezek mint vetületek igazak, de a valóság a térbeli tojás, amelynek köbtartalma van. Ilyen változékony képeket figyelünk meg, ha egy mozgásjelenséghez csak méterrúddal vagy csak órával közeledünk. A valóság az összeolvadt tér és idő: a téridő.