Kezdőlap


Cím:	1973. évi fizika OKTV feladatai
Füzet:	1973/október, 81. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai

1. Az

m_{1} = 30 kg

tömegű,

r = 8 cm

sugarú henger

m_{2} = 60 kg

tömegű deszkán fekszik (1. ábra a rajza). A deszka és a talaj között a surlódás elhanyagolható, a henger és a deszka között a súrlódási együttható

μ = 0, 1

. A hengert

2

másodpercig húzzuk vízszintes irányú,

F = 4, 5 kp

állandó erővel. Mennyi munkát végeztünk? (A csúszási és tapadási súrlódás együtthatóját vegyük egyenlőnek.)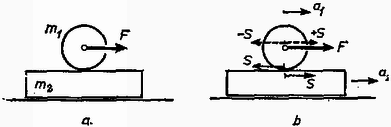

1. ábra

Megoldás. A talajhoz képest a henger középpontjának lineáris gyorsulása

a_{1}

, a deszkáé

a_{2}

(1. ábra b rajza). Az

S

súrlódási erő a hengert hátra, a deszkát előre húzza. Newton II. törvénye szerint a deszkára nézve:

S = a_{2} m_{2}

. A henger középpontjában hozzáveszünk

\pm S

erőket. Közülük

- S

a húzóerő ellen dolgozik, a henger középpontját

F - S

erő gyorsítja, és a henger középpontjára nézve Newton II. törvénye:

F - S = a_{1} m_{1}

. A

\pm S

-ből és

S

-ből álló erőpár

S r

forgatónyomatéka a

Θ

tehetetlenségi nyomatékú hengert

β = (a_{1} - a_{2}) / r

szöggyorsulással forgatja, a forgó mozgás alaptörvénye szerint:

\begin{matrix} \frac{a_{1} - a_{2}}{r} = \frac{S r}{Θ} . \end{matrix}

Három egyenletből álló egyenletrendszerünket megoldjuk

a_{1}

a_{2}

és

S

-re. A megoldás:

\begin{matrix} a_{1} & = \frac{F}{m_{1}} \cdot \frac{m_{1} + m_{2} m_{1} r^{2} / Θ}{m_{1} + m_{2} (1 + m_{1} r^{2} / Θ)}, \\ a_{2} & = \frac{F}{m_{1} + m_{2} (1 + m_{1} r^{2} / Θ)}, \\ S & = F \cdot \frac{m_{2}}{m_{1} + m_{2} (1 + m_{1} r^{2} / Θ)}, \end{matrix}

A mi esetünkben

m_{1} r^{2} / Θ = 2

F = 4, 5 kp = 44, 1

newton,

a_{1} = 1, 05 {m/s}^{2}

a_{2} = 0, 21 {m/s}^{2}

S = 12, 6

newton. Az út

2

másodperc alatt

s = a_{1} t^{2} / 2 = 2, 1

méter, a munkavégzés

W = F s = 92, 61 joule = 0, 45

mkp. A lehetséges maximális súrlódási erő

μ m_{1} g = 29, 4

newton, ez nagyobb, mint

S

, tehát tiszta gördülés van.

2. Elég hosszú lejtőn nagy, zárt doboz csúszik le. Hogyan ‐ milyen kísérletekkel, illetve mérésekkel ‐ állapíthatja meg a doboz belsejében levő észlelő a lejtő

α

hajlásszögét és a csúszási súrlódási együtthatót? (2. ábra a rajza.)
(Párkányi László)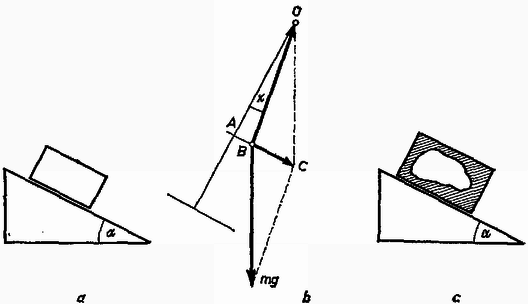

2. ábra

Megoldás. Egy függőónt akasztunk a mennyezetre és megmérjük a padló merőlegesével alkotott

x

szöget (2. ábra b rajza). A függőón tömegére ható

m g

súlyerő és

F

fonálerő eredőjének kell létrehoznia az

m g (sin α - μ cos α)

gyorsító erőt

(B C)

\begin{matrix} tg x = A B / A O = (A C - B C) / A O = \frac{m g sin α - m g (sin α - μ cos α)}{m g cos α} = μ . \end{matrix}

Tehát

x

a súrlódási határszög, és ezzel ismerjük a súrlódási együtthatót:

μ = tg x

. Az

α

meghatározására több módszer van, például az inga lengésidejéből vagy

F

fonálerőt lemérve:

\begin{matrix} F^{2} = {(m g cos α)}^{2} + {(μ m g cos α)}^{2} . \end{matrix}

Innen

cos α = F cos x / m g

.
Mindez azonban csak akkor végezhető el, ha ismerjük

g

számértékét, és biztosra vesszük, hogy a doboz padlója párhuzamos a lejtő hosszával. Ha ez nincs így (2. ábra c rajza), akkor a keresett mennyiségeket nem tudjuk meghatározni.

3. Az

R = 1 m

sugarú,

m = 20 kg

tömegű korong vízszintes pályán, egyenesben gurulhat (3. ábra a rajza). A ráerősített

r = 0, 5 m

sugarú dobról lecsavarodó fonálon

m_{0} = 40 kg

tömegű test lóg. Mekkora gyorsulással halad a korong középpontja, amikor a fonál már véglegesen felvett egy állandó

α

-szögű helyzetet?
(Wiedemann László)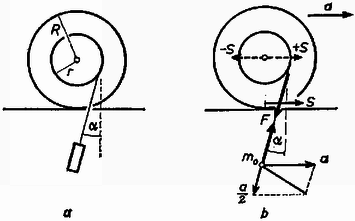

3. ábra

Megoldás. A fonálban

F

erő működik, ezzel az erővel forgatja az

m_{0}

tömeg a hengert, és

F

erő húzza ferdén felfelé az

m_{0}

tömeget (3. ábra b rajza). A henger középpontja

a

gyorsulással mozog jobbfelé.

m_{0}

tömeg gyorsulásának vízszintes összetevője is

a

, ezenkívül a fonál irányában

a / 2

gyorsulással ereszkedik lefelé (

m_{0}

eredő gyorsulása

a

-ból és

a / 2

-ből tevődik össze). A henger alján

S

súrlódási erő működik és középpontjában felveszünk

\pm S

erőket. A henger középpontját

F sin α

erő visszahúzza.
A henger középpontjának haladó mozgására felírt Newton II. törvény:

\begin{matrix} S - F sin α = m a . \end{matrix}

A hengert

F r - S R

forgatónyomaték

β = a / R

szöggyorsulással forgatja, a forgás alaptörvénye szerint:

\begin{matrix} \frac{a}{R} = \frac{F r - S R}{Θ} . \end{matrix}

A lelógó

m_{0}

tömeg haladó mozgására felírt Newton II. törvény a vízszintes összetevőt tekintve:

\begin{matrix} F sin α = m_{0} a - m_{0} \cdot \frac{a}{2} \cdot sin α, \end{matrix}

a függőleges összetevőt tekintve:

\begin{matrix} m_{0} g - F cos α = m_{0} \cdot \frac{a}{2} \cdot cos α . \end{matrix}

Ezt a négy egyenletből álló egyenletrendszert kell megoldanunk

a

α

F

és

S

-re. Mivel a számítás elég bonyodalmas, érdemes az adatokban rejlő egyszerűsítési lehetőségeket felhasználni. A mi esetünkben

m_{0} = 2 m

R = 2 r

Θ = 0, 5 m R^{2}

. Ezeket felhasználva az egyenletrendszer:

\begin{matrix} S - F sin α & = m a, \\ F - 2 S & = m a, \\ F sin α = 2 m a & - m a sin α, \\ 2 m g - F cos α & = m a cos α . \end{matrix}

Ebből

α

-ra ezt az egyenletet kapjuk:

\begin{matrix} sin^{2} α - 4 sin α + 1 = 0. \end{matrix}

Innen

sin α = 2 - \sqrt[]{3} = 0, 268, α = 15, 55^{\circ}

.

Azután következik a többi ismeretlen:

\begin{matrix} a & = g tg α = 0, 2783 g = 2, 727 {m/s}^{2}, \\ F & = m g (2 sec α - tg α) = \\ = 352 newton = 35, 97 kp, \\ S & = m g tg α (3 - sin α) = \\ = 149 newton = 15, 19 kp . \end{matrix}

A II. forduló feladatai:

1. A

4

. ábra

a

rajzán látható elrendezésben kettős ingát készítünk. Az

O_{1}

pont körül lengő,

L_{1} = 60 cm

hosszú,

m_{1} = 0, 2 kg

tömegű lécre

O_{2}

-ben van csapágyazva az

L_{2} = 40 cm

hosszú,

m_{2} = 0, 1 kg

tömegű léc. Mekkora az

O_{1} O_{2}

távolság, ha a két inga úgy leng együtt, hogy a lécek hossztengelyei fedésben maradnak?
(Bodó Zalán)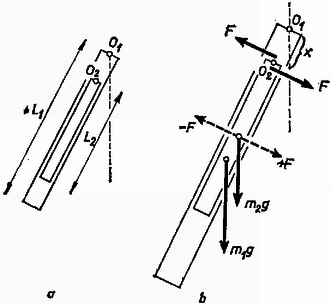

4. ábra

Megoldás. Egy fizikai inga mozgását a súlypont (körív menti), érintőleges haladó mozgásának és a súlypont körüli forgás eredőjének lehet tekinteni. Mindegyikkel külön foglalkozunk.

O_{2}

pontban az ingák kölcsönösen erőt fejtenek ki egymásra, most csak az erők lécre merőleges összetevőjével foglalkozunk. A kis inga a nagy ingát

F

erővel emeli, a nagy inga a kicsi csapágyát

F

erővel lehúzza. A kis inga súlypontjában felvesszük

\pm F

erőket. Az ingák együttlengése azt jelenti, hogy szöggyorsulásuk minden helyzetben egyenlő.
A kis inga, súlypontjának haladó gyorsulását mint a szöggyorsulás és rádiusz szorzatát felírva, használjuk fel Newton II. törvényét (4. ábra b rajza):

\begin{matrix} m_{2} g sin α + F = β (\frac{L_{2}}{2} + x) m_{2} . \end{matrix}

A kis ingára felírjuk a forgómozgás alaptörvényét (a tehetetlenségi nyomatékot a súlypontra nézve kell felírni):

\begin{matrix} β \cdot \frac{L_{2}^{2}}{12} \cdot m_{2} = - F \cdot \frac{L_{2}}{2} . \end{matrix}

A nagy ingánál a forgómozgás alaptörvényét

O_{1}

-re vonatkoztatva írjuk fel:

\begin{matrix} β \cdot \frac{L_{1}^{2} m_{1}}{3} = \frac{L_{1}}{2} \cdot m_{1} g sin α - F x . \end{matrix}

Három egyenletünk van négy ismeretlenre (

F

x

β

és

sin α

). Mivel

β

és

sin α

egyenesen arányosak, az egyenletrendszert meg tudjuk oldani

x

-re:

\begin{matrix} x = \frac{2 L_{1} m_{1} (L_{1} - L_{2})}{3 L_{1} m_{1} + L_{2} m_{2}} = 2 L_{1} \cdot \frac{L_{1} / L_{2} - 1}{3 L_{1} / L_{2} + m_{2} / m_{1}} . \end{matrix}

Számadatainkkal

L_{1} / L_{2} = 3 / 2

m_{2} / m_{1} = 1 / 2

x = L_{1} / 5 = 12

cm.

2. Az

1 {dm}^{2}

alapterületű,

11, 2 dm

magasságú hengerben

8 kg

tömegű, dugattyút tartunk

5, 6 dm

magasságban (5. ábra). A henger fala hőszigetelő. A hengerben

1

mól

273^{\circ} C

hőmérsékletű hélium van. A dugattyút elengedjük. Milyen magasra repül fel? A hélium fajhője állandó térfogaton

C_{v} = 3 cal/mólfok

, állandó nyomáson

C_{p} = 5 cal/mólfok

. Kívül

1

atmoszféra nyomású levegő van. A súrlódástól eltekintünk.
(Vermes Miklós)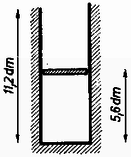

5. ábra

Megoldás. A gáz adiabatikusan terjed ki, az erre érvényes összefüggés:

T V^{κ - 1} = konstans

. Az adatokból látszik, hogy

κ = 5 / 3

. Amíg a dugattyú a hengerben van, a változás adiabatikus, törvényünk szerint:

\begin{matrix} 546 \cdot 5, 6^{2 / 3} = T {(2 \cdot 5, 6)}^{2 / 3} . \end{matrix}

Innen a gáz hőmérséklete abban a pillanatban, amikor a dugattyú a henger tetejére érkezett:

T = 344

K. A gáz energiájának csökkenése:

\begin{matrix} C_{v} (546 - 344) = C_{v} \cdot 202 = 606 cal \approx 2536 joule . \end{matrix}

Ebből lesz a munkavégzés a külső levegő nyomása ellen, amíg a dugattyú a henger tetejére ér:

\begin{matrix} 10, 12 \frac{newton}{{cm}^{2}} \cdot 100 {cm}^{2} \cdot 0, 56 m = 567 joule, \end{matrix}

továbbá a

8

kg emelési munkája kezdeti helyzete fölé

x

méter magasságra:

8 \cdot 9, 8 \cdot x

. Az energiatörvény szerint:

\begin{matrix} 2536 = 567 + 8 \cdot 9, 8 \cdot x, \end{matrix}

innen

x = 25, 1

méter a henger közepétől számítva.

3. A 6. ábra szerinti kapcsolási rajzunkban

C = 2 μ

F-os kondenzátort,

R = 1 kiloohmos

ellenállást jelent,

R_{x}

ismeretlen ellenállás. Az

A B

pontokra váltófeszültséget kapcsolunk. Mi a feltétele annak, hogy a

P Q

pontokra kapcsolt érzékeny fejhallgató ne jelezzen feszültséget?
(Bodó Zalán)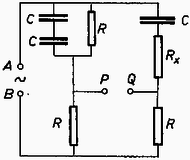

6. ábra

Megoldás. A két ágban a felső részek ellenállásainak és fáziskülönbségeinek meg kell egyeznie. Baloldalt a fázissietés

tg φ = R ω C / 2

, a jobboldalt

tg φ = \frac{1 / ω C}{R_{x}}

, ezeket egyenlővé téve:

\frac{R ω C}{2} = \frac{1}{ω C R_{x}}

. Innen

ω = \frac{1}{C} \cdot \sqrt[]{\frac{2}{R R_{x}}}

. Az ellenállásokat egyenlővé téve:

\begin{matrix} \frac{1}{\sqrt[]{{(\frac{ω C}{2})}^{2} + \frac{1}{R^{2}}}} = \sqrt[]{{(\frac{1}{ω C})}^{2} + R_{x}^{2}} . \end{matrix}

Tulajdonképpen egyenletrendszert kaptunk

ω

-ra és

R_{x}

-re. A második egyenletet rendezve és

ω

-ra felhasználva előbbi eredményünket, nyerjük:

\begin{matrix} 4 R_{x}^{2} + 4 R R_{x} - 3 R^{2} = 0, \end{matrix}

innen

R_{x} = R / 2 = 0, 5

kiloohm, továbbá

ω = 2 / C R = 1000 s^{- 1}

, illetőleg

n = 159 s^{- 1}

III. (kísérleti) forduló.

A II. forduló dolgozatai alapján 15 versenyző kísérletező versenyen vett részt Budapesten az ELTE természettudományi karának Kísérleti Fizikai Intézetében. Fizikai fénytani feladattal foglalkoztak: rés, optikai rács és kettős prizma interferenciajelenségeit kellett tanulmányozniuk.
Az 1973. évi fizikai tanulmányi verseny eredménye:

I. díj: Tegze Miklós (Budapest, Kölcsey F. Gimn. IV. o. t., tanára: Tóth László).
II. díj: Vladár Károly (Kiskunhalas, Szilády Á. Gimn. III. o. t., tanára: Péter Irén).
III. díj: Pálfalvi György (Győr, Révai M. Gimn. III. o. t., tanára: Székely László).

A további helyezettek: 4. Kovács Balázs (Budapest, Apáczai Csere Gimn. IV. o. t., Holics László), 5. Bóc István (Budapest, Apáczai Csere Gimn. IV. o. t., Holics László), 6. Bari Ferenc (Csongrád, Batsányi Gimn. IV. o. t., Szucsán András), 7. Prőhle Péter (Budapest, Fazekas Gimn. III. o. t., Szűcs Barna), 8. Hanyecz Pál (Szentes, Erősáramú Szakközépiskola IV. o. t., Győri Antal), 9. Koltai Ferenc (Budapest, I. István Gimn. IV. o. t., Moór Agnes), 10. Mester János (Csongrád, Batsányi gimn. IV. o. t., Szucsán András).