|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az Eötvös Loránd Fizikai Társulat október 21-én rendezte ez évi fizikai versenyét Budapesten és 7 vidéki városban az idén érettségizettek és középiskolai tanulók számára, A versenyzők 5 óráig dolgozhattak és bármilyen segédeszközt használhattak. A versenyzők létszáma 309 volt. Ismertetjük a feladatokat és megoldásukat.
1.Egy félhengerre olyan hosszú fonalat fektetünk, amelyhez tartozó középponti szög -os (1. ábra). A felszínhez feszülő fonál egyik végén kg-os, másik végén kg-os tömeg van. A fonalat úgy helyezzük el, hogy az kg-os tömeg a félhenger fele magasságában legyen. Ezután elengedjük a fonalat. Melyik tömeg repül le előbb, a hengerről? A súrlódást nem vesszük figyelembe.
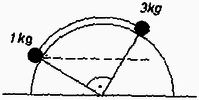 1. ábra
Megoldás. Határozza meg a tömegek helyzetét szög (2. ábra).
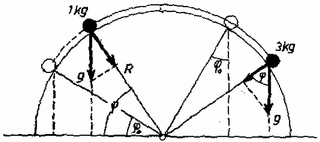 2. ábra
Az indulási helyzetet meghatározó szög . Csak jobbra történő mozgással foglalkozunk. Legyen a két tömeg , ill. .
A fonállal összekötött tömegek egyensúlya olyan szögnél valósul meg, amelyre a jobb oldali tömeg súlyának forgatónyomatéka egyenlő a bal oldali tömeg súlyának forgatónyomatékával. innen , . Tehát feladatunk -os adata mellett a tömegek elindulnak jobb felé.
Mozgás közben, egy bizonyos -hez tartozó helyzetben a tömegek közös sebessége . Az energiatörvény szerint a jobb oldali tömeg munkavégzése egyenlő a bal oldali tömeg helyzeti energiájának növekedésével, hozzáadva az egész szerkezet mozgási energiáját: | |
Innen kifejezzük függvényeként sebességet, illetve centripetális gyorsulást: | | (I.) |
Ez a centripetális gyorsulás -tól -ig monoton növekszik, ha -t - tól -ig változtatjuk.
A bal oldali tömeget erő szorítja a hengerhez. Az elrepülés feltétele, hogy centripetális erő elérje ezt az értéket, vagyis, a gyorsulásokkal kifejezve: A bal oldali tömeg elrepülésének szögét kiszámíthatjuk, ha (II.)-ben felhasználjuk (I.)-szerinti értékét: | |
A összefüggést felhasználva és rendezve:
Ennek megoldása: | |
A mi -os indításunk esetében , tehát az ehhez tartozó helyzetben repülne le a bal oldali tömeg.
A jobb oldali tömegre vonatkozó számítást hasonlóan végezzük el. A tömeg centripetális gyorsulásának a súlyerő összetevőjét kell elérnie, ezért most az elrepülés feltétele: A jobb oldali tömeg elrepüléséhez tartozó szöget iszámíthatjuk, ha (III.)-ban felhasználjuk (I.) szerinti értékét: | |
Ismét használjuk a összefüggést és rendezzük az egyenletet: | |
Az egyenlet megoldása: | |
A mi esetünkben indítási szög mellett a jobb oldali tömeg elrepülési helyzetét meghatározó szög . Tehát a jobb oldali tömeg előbb repül le a hengerről.
Jó áttekintést nyújt a 3. ábra.
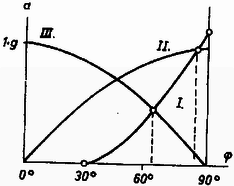 3. ábra
A II. görbe feltünteti függvényében a bal oldali tömeget a hengerhez szorító erőnek megfelelő gyorsulást (sinus-görbe), a III. görbe pedig ugyanezt a jobb oldali tömegnél (cosinus-görbe). Az I. görbe a tömegek közös centripetális gyorsulását mutatja függvényében, -os indítás esetében. A metszéspontok jelentik a lerepülési helyzetet. Látjuk, hogy a jobb oldali tömegnek feltétlenül le kell repülnie valamilyen szögnél. mert az I.-görbe feltétlenül metszi a III.-cosinus-görbét. A II.-görbén nem kapunk feltétlenül metszéspontot. Meghatározható, hogy -os indításnál éri el I. Az értéket, tehát ennél magasabb indításnál a bal oldali tömeg nem repülhet le.
Ha a mozgás elemzése nélkül csak a feladat feltett kérdésére akarunk válaszolni, akkor legegyszerűbben így járhatunk el. A tömegek sebessége és centripetális gyorsulása egyenlő. Ha a bal oldali tömeg a -os helyzetig még nem repült le, akkor ezután a jobb oldali tömegnek kell előbb lerepülnie, mert ekkor már a sinus kisebb, mint a cosinus. Arról egyszerű számítással gyorsan meg lehet győződni, hogy a -os helyzetig a bal oldali tömeg még nem repül le.
2. a) Hosszú szárú -alakú csőben szobahőmérsékletű víz van (4. ábra).
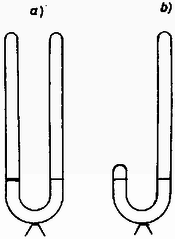 4. ábra
A bal oldali szárban a víz felszínét párolgásmentes olajhártya zárja el. A berendezést súlypontja alatt megtámasztjuk, majd egyenletesen felmelegítjük. Felborul-e?
b) Mi történik melegítéskor az előzőleg kiegyensúlyozott berendezéssel akkor, ha nincs olajhártya, de a bal oldali szár sokkal rövidebb?
Megoldás. a) A jobboldali csőben növekszik a folyadék felett a telített gőzök nyomása (a tenzió) és vizet nyom át a bal oldali szárba. Az ék fölötti keresztmetszetben anyag vándorolt bal felé, és ennek az ilyen alakú eszközben az a következménye, hogy a berendezés felső végével bal felé billen.
b) A melegítés után is egyenlők a tenziók, tehát a két szárban most is egyenlő magasan áll a víz (bár a mostani szint valamivel alacsonyabb, mint az előbbi, mert folyadéknak el kellett párolognia). A hosszabb jobb oldali szárba több gőznek kellett belepárolognia, mint a rövidebb baloldaliba, a jobb oldal nehezebb lett, aminek az a következménye (az egyenlő erőkarok mellett), hogy a szerkezet felső végével jobbra billen.
Megjegyzések. ) esetben a gőz viszonylag kis sűrűsége folytán nem túl nagy a keletkező súlykülönbség. Érdekes még, hogy gőzök nyomása és sűrűsége a felszíntől felfelé menve kissé csökken a magasságkülönbség folytán, amint az a légkörben ismeretes (hipszometriás nyomás- és sűrűségcsökkenés). Tehát a tér csak közvetlenül a felszín mellett telített, feljebb már nem. A kétoldali folyadékszintek magasságára nézve a felszín melletti nyomás a lényeges, és így a szintmagasságok egyenlők maradnak annak ellenére, hogy nagyobb tömegű gőz van a jobb oldali felszín felett. De ezek fent, belülről kisebb erővel nyomják a cső tetejét, mint a bal oldali rövidebb csőben.
Ha eredetileg levegő is lett volna a csövekben, vagy melegítéskor túllépnénk a kritikus hőmérsékletet, az egyensúlymegbomlás előjele ugyanolyan marad.
3. Felfújt, könnyű műanyag labdát találomra megpörgetve sima vízfelületre ejtünk. Azt tapasztaljuk, hogy mielőtt megáll, rendszerint függőleges tengely körül forog. Mi a jelenség magyarázata?
Megoldás. A ferde helyzetű tengely körüli forgás vízszintes és függőleges tengely körüli forgás eredőjeként fogható fel. A vízszintes tengely körüli forgást a súrlódás erősen fékezi, mert a kerület, a gömb "egyenlítője'' mentén nagy a sebesség. A függőleges tengely körüli forgással az érintkező felület kis sebessége jár együtt a gömb kis gömbsüvegénél, tehát ez a forgás lassabban fékeződik, tovább marad meg, a forgás végén már csak ez érvényesül.
A verseny eredménye. I. díjat nyert Szabó Zoltán honvéd (a budapesti Apáczai Csere Gimnáziumban érettségizett mint Turtóczky Sándor tanítványa); II. díjat nyert Németh Tibor, a budapesti Berzsenyi Gimnázium III. osztályában Hubert Györgyné tanítványa; egyenlő helyezésben III. díjat nyertek Bezdek Károly, a dunaújvárosi Münnich Gimnázium IV. o. tanulója (tanára Kobzos Ferenc), Tóth Péter, a budapesti Eötvös Gimnázium IV. o. tanulója (tanára Veres Mihályné) és Vassel Róbert, a budapesti ELTE-TTK matematikus hallgatója (a budapesti I. István Gimnáziumban érettségizett mint Moór Ágnes tanítványa). Dicséretet kaptak könyvjutalommal Nagy Péter honvéd (a budapesti Petőfi Gimnáziumban érettségizett mint Biró István tanítványa), Tarjányi László, a kecskeméti Katona Gimnázium IV. o. t. (tanára Fodor István) és Veress Tibor, a budapesti Radnóti Gimnázium IV. o. t. (tanára, Kugler Sándorné). |
 PDF | MathML
PDF | MathML 


