Kezdőlap


Cím:	Kepler-mozgás ‐ Gravitációs törvény
Szerző(k):	Györgyi Géza
Füzet:	1972/november, 167 - 171. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A III. osztályos gimnáziumi fizikakönyv megemlíti (a 116. lapon), hogy Kepler három bolygótörvényéből a Newton‐féle gravitációs törvény levezethető.
Ebben a cikkben megmutatjuk, miképpen látható be a középiskolai matematika eszközeinek segítségével, hogy a bolygókra a Naptól mért távolság négyzetével fordítottan arányos erő hat.

A Kepler‐mozgás származtatása körmozgásból. Vegyünk fel a síkban két merőleges egységvektort, i-t és j-t. (Ha i-t pozitív irányban

\frac{π}{2}

szöggel elforgatjuk, az így kapott vektor legyen egyenlő j-vel. A szögeket radiánokban mérjük.)
Az

\begin{matrix} x = a [(cos u) i + (sin u) j] \end{matrix}

(1)

vektor

P

végpontja ‐ ha

u

tetszés szerint változhat,

a

pedig állandó ‐ körpályán mozog, melynek sugara

a

(1. ábra).

1. ábra

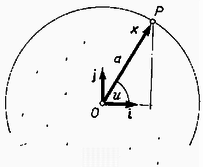Származtassunk e körből ellipszist összenyomással, szakszerűbben szólva

b / a

arányú merőleges affinitással

(0 < b / a ≦ 1)

; az affinitás tengelye legyen a kör i irányvektorú átmérője. A

P

pont képe az

\begin{matrix} y = a (cos u) i + b (sin u) j \end{matrix}

(2)

helyvektorú

Q

pont (2. ábra).

2. ábra

Míg

P

a

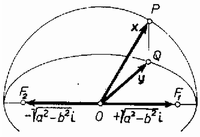sugarú kört futja be,

Q

ellipszispályán halad végig. Ezen ellipszis fél nagytengelye

a

, fél kistengelye

b

; az

a

sugarú kör az ellipszis főköre.

Megmutatható, hogy a

Q

pontnak a

\sqrt[]{a^{2} - b^{2}} i

helyvektorú

F_{1}

, és a

- \sqrt[]{a^{2} - b^{2}} i

helyvektorú

F_{2}

pontoktól mért távolság‐összege állandó s egyenlő

2 a

-val;

F_{1}

és

F_{2}

az ellipszis gyújtópontjai vagy fókuszai.

Q

tehát ellipszispályán kering, mint a bolygók Kepler 1. törvénye szerint. E törvény kimondja még, hogy a Nap a pálya egyik gyújtópontjában van.

Kepler időegyenlete. A következőkben összefüggést vezetünk le az

u

szög s a

t

idő között Kepler 2. törvénye alapján. Ez megállapítja, hogy a Napot (az egyik fókuszt) a bolygóval összekötő vezérsugár által

t

idő alatt súrolt terület egyenesen arányos

t

-vel.
Vizsgáljuk először a körmozgást végző

P

pontot. Növekedjék a

t

idő alatt az x vektor irányszöge zérusról az

u

értékre; x eközben

\frac{1}{2} a^{2} u

területű körcikket súrol. Mekkora az a terület, amelyen ez idő alatt az ellipszis jobb oldali

F_{1}

gyújtópontjából

P

-hez vont

F_{1} P

egyenes szakasz seper végig? (Lásd a 3. ábrát.)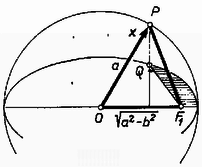

3. ábra

Ezt úgy kapjuk meg, hogy a körcikk

\frac{1}{2} a^{2} u

területéből levonjuk az

O F_{1} P

háromszög területét. Az előző szakaszban láttuk:

F_{1}

távolsága az

O

középponttól

\sqrt[]{a^{2} - b^{2}}

; ez a háromszög alapja. Magassága

a sin u

; a levonandó terület tehát

\frac{1}{2} \sqrt[]{a^{2} - b^{2}} a sin u

. Az

F_{1} P

egyenes szakasz eszerint

t

idő alatt

\frac{1}{2} a^{2} (u - ε sin u)

területet súrol, ahol

ε = \sqrt[]{a^{2} - b^{2}} / a

.
Az a terület, melyet az

F_{1}

fókuszból az ellipszispályán haladó

Q

-hoz húzott

F_{1} Q

egyenes szakasz súrol a

t

idő alatt (a 3. ábrán vonalkázva), az előbb említett területből

b / a

arányú összenyomással kapható. Számértéke az előbbiének

b / a

-szorosa:

\begin{matrix} \frac{1}{2} a b (u - ε sin u) . \end{matrix}

(3)

(Egy

A

területű síkidomból

λ

arányú összenyomással kapott síkidom területe

λ A

. Ezt könnyen beláthatjuk pl. háromszög esetében, de igaz bármilyen síkidomra.)
Annak feltétele, hogy az

F_{1}

gyújtópontból

Q

-hoz vont

F_{1} Q

,,vezérsugár'' által

t

idő alatt súrolt terület

t

-vel arányos legyen:

\begin{matrix} u - ε sin u = ω t, \end{matrix}

(4)

ahol

ω = 2 π / T

állandó;

T

az az idő, mely alatt

u

zérusról

2 π

-re nő (keringési idő). Ez az összefüggés biztosítja, hogy

Q

ellipszispályáján a 2. Kepler‐törvénynek megfelelően kering; (4) neve: Kepler időegyenlete.

A sebesség. Határozzuk meg a Kepler‐mozgást végző

Q

pont sebességét. Az

u

szögnek megfelelő

t

időt részletesebben

t (u)

-val jelöljük, y helyett is

y (u)

-t írunk. Ha

u

-t megnöveljük

Δ u

-val, az y vektor

y (u + Δ u) = y (u) + Δ y

-ra,

t (u)

pedig

t (u + Δ u) = t (u) + Δ t

-re változik. A

Δ y / Δ t

átlagsebesség‐vektort így írjuk fel:

\begin{matrix} \frac{Δ y}{Δ t} = \frac{Δ u}{Δ t} \frac{Δ y}{Δ u} . \end{matrix}

(5)

Az y vektort (2) mint

u

függvényét adja meg,

u

és

t

között (4) ad kapcsolatot. Ezen összefüggések alapján (5) jobb oldalának két tényezőjét így írhatjuk:

\begin{matrix} \frac{Δ u}{Δ t} = \frac{ω}{1 - ε \frac{Δ sin u}{Δ u}}, \frac{Δ y}{Δ u} = a \frac{Δ cos u}{Δ u} i + b \frac{Δ sin u}{Δ u} j; \end{matrix}

(6)

itt

Δ cos u = cos (u + Δ u) - cos u

Δ sin u = sin (u + Δ u) - sin u

. Ezeket a kifejezéseket helyettesítsük be (5)-be.
A sebességet a

t

pillanatban az átlagsebesség határértéke adja meg:

\begin{matrix} v = {lim}_{Δ t \to 0}^{} \frac{Δ y}{Δ t} . \end{matrix}

(7)

A harmonikus rezgőmozgás sebességének és gyorsulásának meghatározásakor megtanultuk, mi a határértéke

cos u

és

sin u

differenciahányadosának:

\begin{matrix} {lim}_{Δ u \to 0}^{} \frac{Δ cos u}{Δ u} = - sin u, {lim}_{Δ u \to 0}^{} \frac{Δ sin u}{Δ u} = cos u . \end{matrix}

(8)

Az (5), (6), (7), (8) egyenleteket felhasználva kapjuk:

\begin{matrix} v = \frac{ω}{1 - ε cos u} [- a (sin u) i + b (cos u) j] . \end{matrix}

(9)

A gyorsulás. A következőkben a Kepler‐mozgást végző

Q

pont gyorsulását határozzuk meg.
Előkészítésképpen bevezetjük az

\begin{matrix} r = y - \sqrt[]{a^{2} - b^{2}} i \end{matrix}

(10)

vektort, mely az

F_{1}

fókuszt

Q

-val (a Napot a bolygóval) köti össze (4. ábra).

4. ábra

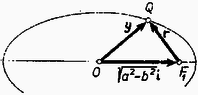A (2) kifejezés és a

\sqrt[]{a^{2} - b^{2}} = ε a

egyenlőség felhasználásával r-et így írhatjuk:

\begin{matrix} r = a (cos u - ε) i + b (sin u) j . \end{matrix}

(11)

Számítsuk ki ezen vektor r hosszát. Képezve az egymásra merőleges összetevők hosszának négyzetösszegét, Pitagorasz tétele értelmében kapjuk:

\begin{matrix} r = \sqrt[]{a^{2} {(cos u - ε)}^{2} + {(b sin u)}^{2}} = \sqrt[]{a^{2} (ε^{2} cos^{2} u - 2 ε cos u + 1)} = a (1 - ε cos u); & (12) \end{matrix}

itt a

cos^{2} u + sin^{2} u = 1

azonosság segítségével

sin^{2} u

-t

cos^{2} u

-val fejeztük ki, majd felhasználtuk a

\sqrt[]{a^{2} - b^{2}} = ε a

egyenlőséget, végül a négyzetgyökvonás elvégzésekor figyelembe vettük, hogy

ε cos u

sohasem nagyobb 1-nél.
Rátérünk a gyorsulás kiszámítására. Mialatt a

t

idő

t + Δ t

-re növekszik, az

u

szög

Δ u

-val nő; v megváltozását a

Δ t

időtartam folyamán jelöljük

Δ v

-vel. A v sebesség (9) kifejezésének felhasználásávala

Δ v / Δ t

átlaggyorsulást így írhatjuk fel:

\begin{matrix} \frac{Δ v}{Δ t} = \frac{ω}{Δ t} {- a [\frac{sin (u + Δ u)}{1 - ε cos (u + Δ u)} - \frac{sin u}{1 - ε cos u} i] . + b [\frac{cos (u + Δ u)}{1 - ε cos (u + Δ u)} - \frac{cos u}{1 - ε cos u}] j} . & (13) \end{matrix}

Hozzuk közös nevezőre a szögletes zárójelben álló hányadosfüggvényeket. A közös nevező

[1 - ε cos (u + Δ u)] (1 - ε cos u)

. Az i előtt szorzóként álló szögletes zárójel számlálója

\begin{matrix} sin (u + Δ u) - sin u - ε [sin (u + Δ u) cos u - sin u cos (u + Δ u)], \end{matrix}

(14)

a j előtt állóé

\begin{matrix} cos (u + Δ u) - cos u . \end{matrix}

(15)

Δ sin u = sin (u + Δ u) - sin u

Δ cos u = cos (u + Δ u) - cos u

rövidítésekkel (14) a

\begin{matrix} Δ sin u - ε (cos u Δ sin u - sin u - Δ cos u), \end{matrix}

(16)

(15) a

\begin{matrix} Δ cos u \end{matrix}

(17)

alakban írható fel. Célszerű ezen kívül (13) jobb oldalát

Δ u

-val megszorozni és elosztani. A

Δ v / Δ t

átlaggyorsulás számára ezen átalakítások elvégzése után a következő kifejezést kapjuk:

\begin{matrix} \frac{Δ v}{Δ t} = \frac{Δ u}{Δ t} \frac{ω}{[1 - ε cos (u + Δ u)] (1 - ε cos u)} {+ a [(1 - ε cos u) \frac{Δ sin u}{Δ u} + ε sin u \frac{Δ cos u}{Δ u}] i + b \frac{Δ cos u}{Δ u} j} . & (18) \end{matrix}

A gyorsulást a

t

pillanatban az átlaggyorsulás határértéke adja meg. A

Δ u / Δ t

differenciahányadost (6) alatt felírtuk, a

sin u

és a

cos u

függvény differenciahányadosának határértékét ismerjük [lásd a (8) képletet]. A nevezőben álló

[1 - ε cos (u + Δ u)]

határértéke

(1 - ε cos u)

. A pillanatnyi gyorsulás

\begin{matrix} a = {lim}_{Δ t \to 0}^{} \frac{Δ v}{Δ t} \end{matrix}

(19)

vektora számára így az

\begin{matrix} a = \frac{ω^{2}}{{(1 - ε cos u)}^{3}} [a (cos u - ε) i + b (sin u) j] \end{matrix}

(20)

kifejezést kapjuk (az utolsó lépésben még egyszer figyelembe vettük a

cos^{2} u + sin^{2} u = 1

azonosságot).
A (20) egyenlet jobb oldalán a szögletes zárójelben (11) szerint az r vektor áll, mely

F_{1}

-et

Q

-val (a Napot a bolygóval) köti össze. A nevezőben

1 - ε cos u

pedig (12) értelmében

r / a

-val egyenlő, ahol

r

az r vektornak a hossza. Célszerű lesz bevezetni az

r^{\circ} = (1 / r) r

jelölést (

r^{\circ}

egységvektor, mely az

F_{1}

gyújtópontból

Q

felé mutat). Mindezt felhasználva, az

a

gyorsulásvektor számára kapott (20) kifejezés, ha mind a két oldalát megszorozzuk a bolygó

m

tömegével, a következő alakban írható fel:

\begin{matrix} m a = - m ω^{2} a^{3} \frac{r^{\circ}}{r^{2}} . \end{matrix}

(21)

Newton második mozgástörvénye értelmében a tömeg és a gyorsulás

m a

szorzata egyenlő az erővel. Látjuk: a bolygóra a Naptól mért

r

távolság négyzetével fordítottan arányos erő hat, Newton gravitációs törvényének megfelelően. Ezen erő irányát

a - r^{\circ}

egységvektor határozza meg: az erővektor a bolygótól a Nap felé mutat.
Kepler (4) időegyenletével kapcsolatosan megállapítottuk, hogy

ω = 2 π / T

, ahol

T

a keringési idő. Így tehát

ω^{2} a^{3} = {(2 π)}^{2} (a^{3} / T^{2})

. A 3. Kepler‐törvény kimondja: az

a

fél nagytengely köbének s a

T

keringési idö négyzetének hányadosa a Naprendszer minden bolygójára ugyanaz az érték. (Egyébként más úton meg lehet mutatni, hogy

ω^{2} a^{3} = f M

, ahol

M

a Nap tömege,

f

pedig a bolygó s a Nap tömegétől független állandó.)

Megjegyzés. A fentiekben elkerültük a hivatkozást a különféle (pl. a hánvadosfüggvényre, közvetett függvényre érvényes) deriválási szabályokra. Ezekre hivatkozva a levezetést rövidebbé, gépiesebbé tehetjük.