Kezdőlap


Cím:	Az 1972. évi (6.) Nemzetközi Fizikai Diákolimpia feladatai
Szerző(k):	Éber Nándor , Gács Lajos , Imhof Gyula , Kövér András , Szabó Zoltán
Füzet:	1972/november, 161 - 167. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. feladat. Adva van három henger: az első tömör $(1)$ , a második véges falvastagságú, belül üres cső $(2)$ , a harmadik ugyanakkora falvastagságú cső, de a fallal egyező sűrűségű folyadékkal töltve $(3)$ . A három henger hossza, külső rádiusza és össztömege egyenlő. A második henger anyagának sűrűsége a többi henger sűrűségének $n$ -szerese. A hengereket $α$ hajlásszögű lejtőre tesszük. A súrlódási együttható a henger külső fala és a lejtő között $μ$ . A $3$ . hengernél a folyadék és a henger belső fala között a súrlódás elhanyagolható; a hengert elhanyagolható tömegű síklapok zárják le. Állapítsuk meg és hasonlítsuk össze a hengerek lineáris gyorsulását, szöggyorsulását sima legördülés és csúszva gördülés esetében.

Megoldás. Az

R

rádiuszú henger

m g

súlyából eredő

m g cos α

merőleges nyomóerőt ellensúlyozza a lejtő anyagának rugalmas ereje; ezzel ne is foglalkozzunk (1. ábra).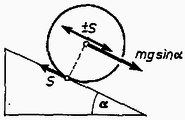

1. ábra

Az érintkezési ponton

S

súrlódási erő hat. A henger középpontjában felveszünk

\pm S

erőket. A henger

a

lineáris gyorsulását okozó erő:

\begin{matrix} m a = m g \cdot sin α - S . \end{matrix}

A hengert

R S

forgatónyomaték

β = a / R

szöggyorsulással forgatja.

Θ

tehetetlenségi nyomaték mellett:

\begin{matrix} \frac{a}{R} = \frac{R S}{Θ} . \end{matrix}

Az egyenletrendszer megoldása adja a lineáris gyorsulást és a működő súrlódási erőt:

\begin{matrix} a & = g sin α \cdot \frac{1}{1 + Θ / m R^{2}}, & (1) \\ S & = m g sin α \cdot \frac{Θ / m R^{2}}{1 + Θ / m R^{2}} . \end{matrix}

Mindez csak sima legördülés esetében érvényes. A súrlódási erő előfordulható legnagyobb értéke

μ m g cos α

. Keressük, ez mikor következik be:

\begin{matrix} μ m g cos α_{h} = m g sin α_{h} \cdot \frac{Θ / m R^{2}}{1 + Θ / m R^{2}} . \end{matrix}

Innen a határeset feltétele:

\begin{matrix} tg α_{h} = μ (1 + m R^{2} / Θ) . \end{matrix}

(2)

Ha ezt a határt túlléptük, a forgás szöggyorsulása:

\begin{matrix} β = \frac{μ m g (cos α) R}{Θ}; \end{matrix}

(3)

a henger középpontjának lineáris gyorsulása ekkor:

\begin{matrix} a = g sin α (1 - μ / tg α) . \end{matrix}

(4)

1) Az első,

ϱ

sűrűségű,

L

hosszúságú henger esetében a tömeg

m = ϱ π R^{2} L

, a tehetetlenségi nyomaték

Θ = 0, 5 m R^{2}

. Sima legördüléskor a lineáris gyorsulás (1)-ből következően:

\begin{matrix} a_{1} = \frac{2 g sin α}{3}, \end{matrix}

(1.1)

a csúszva gördülés határesete (2)-ből:

\begin{matrix} tg α_{h 1} = 3 μ, \end{matrix}

(2.1)

csúszva gördüléskor a szöggyorsulás (3)-ból:

\begin{matrix} β_{1} = 2 μ g cos α / R . \end{matrix}

(3.1)

2) A cső esetében a fal tömege egyenlő az előbbi

m

-mel. A belső üreg

r

rádiuszát a sűrűségek

n

hányadosából számítjuk ki,

ϱ π R^{2} L = n ϱ π L (R^{2} - r^{2})

, innen:

\begin{matrix} r^{2} = R^{2} \cdot \frac{n - 1}{n} . \end{matrix}

A tehetetlenségi nyomaték ennek figyelembevételével:

\begin{matrix} Θ_{2} = 0, 5 n ϱ L π R^{2} \cdot R^{2} - 0, 5 n ϱ L π r^{2} \cdot r^{2} = 0, 5 n ϱ L π (R^{4} - r^{4}) = \\ = 0, 5 n ϱ L π [R^{4} - R^{4} \cdot \frac{{(n - 1)}^{2}}{n^{2}}] = 0, 5 m R^{2} \cdot \frac{2 n - 1}{n} . \end{matrix}

A lineáris gyorsulás a tiszta gördülésnél (1) felhasználásával:

\begin{matrix} a_{2} = g sin α \cdot \frac{2 n}{4 n - 1}, \end{matrix}

(1.2)

a határszög (2)-ből:

\begin{matrix} tg α_{h 2} = μ \cdot \frac{4 n - 1}{2 n - 1}, \end{matrix}

(2.2)

a forgás szöggyorsulása (3)-ból:

\begin{matrix} β_{2} = \frac{2 μ g cos α}{R} \cdot \frac{n}{2 n - 1} . \end{matrix}

(3.2)

3) A folyadékkal telt henger esetében a belső rész nem forog, hiszen súrlódási erő hiányában a folyadék és a fal közötti erő merőleges a falra, így nincs forgatónyomaték, amely a folyadékot forgatná.

m

helyébe az előbbi

m

teljes tömeget kell tennünk, de a tehetetlenségi nyomatékot csak a cső falára nézve kell számítanunk:

\begin{matrix} Θ_{3} = 0, 5 ϱ L π R^{2} \cdot R^{2} - 0, 5 ϱ L π r^{2} \cdot r^{2} = 0, 5 m R^{2} \cdot \frac{2 n - 1}{n^{2}} . \end{matrix}

A lineáris gyorsulás:

\begin{matrix} a_{3} = g sin α \cdot \frac{2 n^{2}}{2 n^{2} + 2 n - 1}, \end{matrix}

(1.3)

a határszög:

\begin{matrix} tg α_{h 3} = μ \cdot \frac{2 n^{2} + 2 n - 1}{2 n - 1}, \end{matrix}

(2.3)

a fal forgásának a szöggyorsulása:

\begin{matrix} β_{3} = \frac{2 μ g cos α}{R} \cdot \frac{n^{2}}{2 n - 1} . \end{matrix}

(3.3)

Következnek az összehasonlítások. A lineáris gyorsulások aránya:

\begin{matrix} a_{1} : a_{2} : a_{3} = \frac{1}{3} : \frac{1}{4 n - 1} : \frac{n^{2}}{2 n^{2} + 2 n - 1} . \end{matrix}

A határszögek tangenseinek aránya:

\begin{matrix} tg α_{h 1} : tg α_{h 2} : tg α_{h 3} = 3 : \frac{4 n - 1}{2 n - 1} : \frac{2 n^{2} + 2 n - 1}{2 n - 1} . \end{matrix}

A szöggyorsulások aránya:

\begin{matrix} β_{1} : β_{2} : β_{3} = 1 : \frac{n}{2 n - 1} : \frac{n^{2}}{2 n - 1} . \end{matrix}

Csúszva gördülés esetében mindegyik henger lineáris gyorsulása egyformán a (4) szerinti érték.
Érdemes megvizsgálni

r

a

tg α_{h}

β

értékeinek változását, ha

n

1-től végtelenig növekszik.

Imhof Gyula

II. feladat. A 2. ábra szerinti elrendezésben az A hengert adiabatikus szigetelőfal, H hengert állandóan

T_{h} = 300 K

hőmérsékletű tartály veszi körül. A hengerek alapterülete egyező. A dugattyúkat merev rúd kapcsolja össze. A dugattyúk súrlódás nélkül, lassan mozoghatnak. A H hengerben

p_{h} = 1

atmoszféra nyomású héliumgáz, az A hengerben

3 mól

argon van, kezdetben

1

atmoszféránál nagyobb

p_{a}

nyomáson. A dugattyúkat elengedve olyan végső egyensúly áll be, amelyben az argon térfogata a kezdeti térfogat

8

-szorosa, vagyis

8 V_{a}

, a hélium sűrűsége a kezdeti érték kétszerese és az állandó hőmérsékletű hőtartály

10 800 cal

-t vett fel. Határozzuk meg a gázok kezdeti és végső adatait!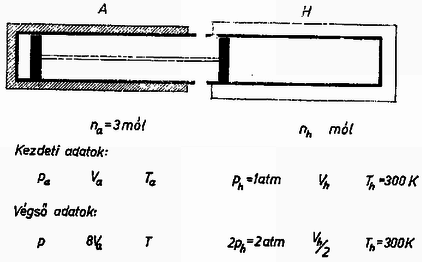

2. ábra

Megoldás. Ha a változatlan hőmérsékletű hélium térfogata feleződött, akkor nyomása megkétszereződött, vagyis a kísérlet végén 2 atmoszféra lett.

Az

n_{h}

mól hélium által felvett hőmennyiség az izotermális változás közben:

\begin{matrix} Q = n_{h} \cdot R T lg (p_{2} / p_{1}) . \end{matrix}

A gázállandó

R = 2

cal/fok értékét és feladatunk adatait használva

10 800 = n_{h} \cdot 2 \cdot 300 \cdot lg 2

, innen a hélium mennyisége

n_{h} = 60

mól. Ennek térfogata a kísérlet kezdetén

V_{h} = 60 \cdot 22, 4 \cdot 300 / 273 = 1477

liter, a kísérlet végén

1477 / 2 = 738, 5

liter. Tehát a héliumról már mindent tudunk.
Az argonra alkalmazzuk a

p V^{ϰ} =

konst adiabatikus törvényt:

\begin{matrix} p_{a} V_{a}^{ϰ} = p {(8 V_{a})}^{ϰ} . \end{matrix}

Vagyis

p_{a} / p = 8^{^{5} /_{3}} = 21, 8

. (Egyatomos gázoknál

ϰ = 5 / 3

). Az argon végső nyomása az egyensúly beálltakor annyi, mint a hélium végső nyomása, vagyis

p = 2

atmoszféra. Kezdeti nyomása

p_{a} = p \cdot 21, 8 = 43, 6

atmoszféra.
A két gáz térfogatváltozása egyenlő. Az argon térfogatnövekedése

8 V_{a} - V_{a} = 7 V_{a}

. A hélium térfogatvesztesége

738, 5

liter, tehát

7 V_{a} = 738, 5

liter,

V_{a} = 738, 5 liter : 7 = 105, 5

liter. Az argon végső térfogata

8 V_{a} = 844

liter.
Az adiabatikus változás törvénye

T V^{ϰ - 1} =

konst alakban is ismeretes. A mi esetünkben:

\begin{matrix} T_{a} V_{a}^{^{2} /_{3}} = T {(8 V_{a})}^{^{2} /_{3}}, vagyis T_{a} / T = 8^{^{2} /_{3}} = 4. \end{matrix}

Az argon adiabatikus kiterjedésekor belső energiájának csökkenése egyenlő a végzett munkával. A mi kísérletünkben ez végső soron a hélium hőtartályába vándorol, róla tudjuk, hogy 10 800 cal. Az argon állandó térfogat melletti moláris fajhője

C_{V} = 3 cal/mól \cdot fok

, tehát:

\begin{matrix} 10 800 = 3 \cdot 3 (T_{a} - T) . \end{matrix}

Innen az argon hőmérsékletére vonatkozó második egyenletünk:

\begin{matrix} T_{a} - T = 1200 K . \end{matrix}

Egybevetve az előbbi

T_{a} / T = 4

egyenlettel az egyenletrendszer megoldása:

\begin{matrix} T_{a} = 1600 K, T = 400 K . \end{matrix}

Szabó Zoltán

Megjegyzés. A külső nyomást illetően a legjobb a hengereken kívül légüres teret elképzelni. Az eredeti feladat adatai nem voltak ügyesen megválasztva, a szöveg is kifogásolható volt. Kérdezték azt is, mi történik, ha a kísérlet után a két gázt összeeresztjük. Az eredmény könnyen kiszámítható. Továbbá az eredeti szöveg az adiabatikus változás törvényének kinetikus levezetését is bekapcsolta a feladatba, aminek szintén nincs akadálya.

III. feladat. Téglalap alakú, függőleges helyzetű feltöltött síkkondenzátort alsó szélével folyékony dielektrikumhoz érintünk (

3

. ábra). Meddig húzódik fel a folyadék a lemezek között? A kapilláris hatás elhanyagolható.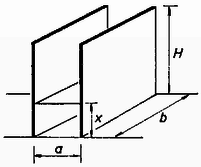

3. ábra

Megoldás. A folyadék sűrűsége

ϱ

, relatív dielektromos állandója

ε

. Eredetileg a kondenzátor kapacitása

k b H / a

. Ha

x

magasságig húzódik fel a folyadék, akkor a részkapacitások alul

ε k b x / a

, felül

k b (H - x) / a

. Kísérlet előtt

U_{0}

, a kísérlet után

U

a lemezek potenciálkülönbsége. A folyadék felszívódása után a töltés ugyanannyi, mint előtte:

\begin{matrix} k b H U_{0} / a = ε k b x U / a + k b (H - x) U / a . \end{matrix}

Innen a kísérlet utáni potenciálkülönbség:

\begin{matrix} U = \frac{H}{H + (ε - 1) x} \cdot U_{0} . \end{matrix}

(5)

A kondenzátor elektromos energiája

0, 5 C U^{2}

. A felszívott folyadék helyzeti energiája

0, 5 ϱ a b x g \cdot x

. A kísérlet után a kondenzátor összes energiája, (5) figyelembevételével:

\begin{matrix} E = \frac{ϱ a b g x^{2}}{2} + \frac{1}{2} [\frac{ε k b x}{a} + \frac{k b (H - x)}{a}] U^{2} = \frac{ϱ a b g x^{2}}{2} + \frac{H^{2} k b U_{0}^{2}}{2 a [H + (ε - 1) x]} . \end{matrix}

Úgy áll be az egyensúlyi helyzet, hogy az összes energia minimum legyen, vagyis teljesülnie kell a következő feltételnek:

\begin{matrix} \frac{d E}{d x} = ϱ a g x - \frac{k b H^{2} U_{0}^{2} (ε - 1)}{2 a {[H + (ε - 1)]}^{2}} = 0. \end{matrix}

Rendezve

x

-re vegyes harmadfokú egyenletet kapunk, amelyet pl. próbálgatással közelítve megoldhatunk.

a

H

méterben,

ϱ

{kg/m}^{3}

-ben,

U_{0}

voltban helyettesítendő,

g = 9, 8 {m/s}^{2}

k = 8, 86 \cdot 10^{- 14}

farad/cm.
Erőhatással leírva az a helyzet, hogy a lemezek között a folyadék határfelületén inhomogén tér alakul ki és ez emeli fel a folyadékot.

Kövér András

IV. feladat.

2 r

átmérőjű,

n_{0}

törésmutatójú anyagból készült vékony bikonvex lencse görbületi sugarai

R_{1}

és

R_{2}

. A lencse egyik oldalán

n_{1}

, a másik oldalán

n_{2}

törésmutatójú anyag van. A szokásos közelítések érvényesek.
a) Bizonyítsuk be, hogy

\begin{matrix} \frac{f_{1}}{t_{1}} + \frac{f_{2}}{t_{2}} = 1, \end{matrix}

ahol

f_{1}

és

f_{2}

a két oldalon mérhető fókusztávolság,

t_{1}

az egyik,

t_{2}

a másik oldalon mért tárgy-, illetve képtávolság.
b) A lencsét síkjára merőlegesen két részre vágjuk szét és a részeket kis

δ

távolságra távolítjuk el. Mindkét oldalon levegő van. A lencse egyik oldalán

t

távolságban pontszerű, monokromatikus fényforrást helyezünk el,

(t > f)

. A lencsétől

H

távolságban levő ernyőn hány interferenciacsík keletkezik?

Megoldás. a) A jelöléseket a 4. ábra tünteti fel.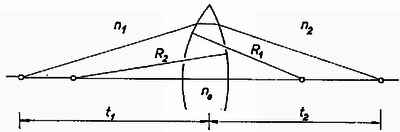

4. ábra

Ismeretes, hogy ilyen általános esetben:

\begin{matrix} \frac{n_{1}}{t_{1}} + \frac{n_{2}}{t_{2}} = \frac{n_{0} - n_{1}}{R_{1}} + \frac{n_{0} - n_{2}}{R_{2}} . \end{matrix}

(6)

(Levezetése megtalálható többek között Vermes Miklós: Fizikai kísérletek ‐ fizikai feladatok c. könyvének 131. oldalán.)
Az

f_{1}

gyújtótávolság az

n_{2}

törésmutatójú anyagból párhuzamosan érkező sugarak találkozási pontjának távolságát jelenti. A

t_{2} = \infty

helyettesítés (6)-ból ezt adja:

\begin{matrix} \frac{n_{1}}{f_{1}} = \frac{n_{0} - n_{1}}{R_{1}} + \frac{n_{0} - n_{2}}{R_{2}}, \end{matrix}

innen:

\begin{matrix} n_{1} = f_{1} [\frac{n_{0} - n_{1}}{R_{1}} + \frac{n_{0} - n_{2}}{R_{2}}] . \end{matrix}

(7)

Hasonlóan az

n_{1}

-ből párhuzamosan érkező sugarakra

t_{1} = \infty

alapján:

\begin{matrix} n_{2} = f_{2} [\frac{n_{0} - n_{1}}{R_{1}} + \frac{n_{0} - n_{2}}{R_{2}}] . \end{matrix}

(8)

(7) és (8) alatti eredményeinket (6)-ban az egyenlet bal oldalán

n_{1}

és

n_{2}

helyére téve és a szögletes zárójelben levő kifejezéssel egyszerűsítve:

\begin{matrix} \frac{f_{1}}{t_{1}} + \frac{f_{2}}{t_{2}} = 1. \end{matrix}

Az eredeti feladat egy speciálisabb esetben kívánta meg a bizonyítást.

n_{1} = n_{2} = 1

esetében a közismert lencsetörvényt kapjuk meg.
b) Az

f

gyújtótávolságú lencse elé

t

távolságba helyezett pontszerű fényforrásról két reális képet kapunk

k = t f / (t - f)

távolságban (5. ábra).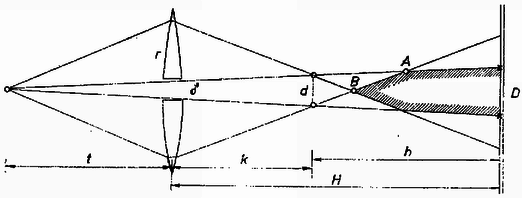

5. ábra

Ha a rés szélessége

δ

, akkor a reális képek egymástól mért távolsága a

d / δ = (t + k) / t

aránypár alapján:

\begin{matrix} d = δ \cdot \frac{t + k}{t} = \frac{δ t}{t - f} . \end{matrix}

(9)

Ez a két reális kép két koherens fényforrás, és közös fénykúpjukban interferenciát figyelhetünk meg. Az ismert fénytani képlet alapján (l. például Fizika a gimn. szakosított III. o. sz., II. kötet 249. oldal) a fényforrásoktól

h

távolságban,

λ

hullámhossz esetében az interferenciacsíkok távolsága:

\begin{matrix} s = \frac{λ h}{d} . \end{matrix}

A mi esetünkben

h = H - k = [H (t - f) - t f] : (t - f)

, továbbá (9) felhasználásával:

\begin{matrix} s = \frac{λ}{δ t} [H - (t - f) - t f] . \end{matrix}

(10)

Felfogó ernyőnkön a közös fénykúp

D

átmérője a

D / δ = (H + t) / t

aránypár alapján:

\begin{matrix} D = δ \cdot \frac{H + t}{t} . \end{matrix}

(11)

Az interferenciacsíkok

N

darabszámát (11) és (10) osztásával kapjuk:

\begin{matrix} N = \frac{D}{s} = \frac{δ^{2}}{λ} \cdot \frac{H + t}{H (t - f) - t f} . \end{matrix}

Számadatok példaképp:

f = 10

cm,

t = 20

cm,

δ = 0, 1

cm,

λ = 0, 5 μ

H = 50

cm,

N = 46, 6

.
Ha az ernyő

A

pontnál közelebb kerül, új számítást kell végeznünk

D

meghatározására.

B

ponton belül nem keletkezik interferencia.

Éber Nándor

V. Kísérleti feladat. Adva van két ugyanazon anyagból készült henger. Külső méreteik megegyeznek. Az egyik tömör, a másikban végig hengeres üreg van, a külső henger tengelyével párhuzamosan. Az elzáró lemezek vékonyak. Határozzuk meg az anyag sűrűségét, az üreg átmérőjét, az üreg és henger tengelyeinek távolságát!

Megoldás. A hengerek anyagának sűrűségét abból határoztam meg, hogy a tömör henger vízen úszva milyen mélyen merült be. (A henger vízszintes tengellyel úszott). Az üreges henger úsztatásával ennek átlagos fajsúlyát határoztam meg. Ebből számítható volt az üreg átmérője. Az üreg tengelyének távolságát úgy határoztam meg, hogy az üreges hengert lejtőre helyeztem és a lejtő hajlásszögét mértem meg a henger elindulásának pillanatában. Ekkor a furat tengelye, a külső henger tengelye és az üreges henger súlypontja egyetlen vízszintes síkban van, továbbá a súlypont függőlegesen az alátámasztási pont fölött van. Így megtudjuk, hogy milyen messze van a súlypont a középtől, és az üreg átmérőjének ismeretében meghatározható a két tengely távolsága.

Gács Lajos