Kezdőlap


Cím:	1972. évi fizika OKTV feladatai
Füzet:	1972/október, 81 - 86. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai:

1. Az

m_{1} = 5 kg

és az

m_{2} = 3 kg

tömegű testek egymástól

s_{1} = 0, 5 méterre

állnak. Az

m_{2}

tömegű test az asztal szélétől

s_{2} = 0, 5 méterre

van. A súrlódási együttható

μ = 0, 102 = 1 / 9, 8

. Mekkora sebességgel kell az

m_{1}

tömegű testet a másik felé elindítani, hogy rugalmas ütközés után a) az

m_{2}

tömegű, b) az

m_{1}

tömegű test épp az asztal széléig jusson el? (1. ábra.)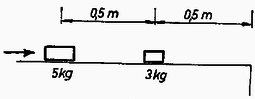

1. ábra

Megoldás. A súrlódás következtében egyenletesen lassuló mozgás jön létre

a = μ g = 1 {m/s}^{2}

negatív gyorsulással. Ha a rugalmas ütközés előtt a tömegek sebessége

v_{1}

és

v_{2}

, akkor a rugalmas ütközés után az

u_{1}

és

u_{2}

sebességek az ütközés törvénye szerint:

\begin{matrix} u_{1} & = \frac{(m_{1} - m_{2}) v_{1} + 2 m_{2} v_{2}}{m_{1} + m_{2}}, \\ u_{2} & = \frac{2 m_{1} v_{1} + (m_{2} - m_{1}) v_{2}}{m_{1} + m_{2}} . \end{matrix}

A mi esetünkben

m_{2}

tömeg kezdeti sebessége

v_{2} = 0

, ezért

\begin{matrix} u_{1} & = \frac{v_{1}}{4}, & (1) \\ u_{2} & = \frac{5}{4} \cdot v_{1} . & (2) \end{matrix}

Továbbá a lassuló mozgás

v = v_{0} - a t

és

s = v_{0} t - a t^{2} / 2

törvényeiből az idő kiküszöbölésével:

\begin{matrix} v = \sqrt[]{v_{0}^{2} - 2 a s} = \sqrt[]{v_{0}^{2} - 1 m^{2} / s^{2}} . \end{matrix}

(3)

Az a) kérdés esetében

m_{2}

érkezik az asztal széléhez

v = 0

sebességgel, tehát indulási sebessége (3) alapján

v_{0} = \sqrt[]{0^{2} + 1} = 1

m/s volt. Ez a rugalmas ütközés

u_{2}

sebessége, tehát (2) alapján

v_{1} = 0, 8

m/s. Ezzel a sebességgel ütközött az

m_{1}

tömeg. Indulási sebessége (3) szerint

\sqrt[]{0, 8^{2} + 1} m/s = \sqrt[]{1, 64} m/s = 1, 28 m/s

volt.
A b) kérdés esetében

m_{1}

érkezik 0 sebességgel az asztal széléhez, tehát (3) szerint az ütközés helyéről

\sqrt[]{0^{2} + 1} = 1 m/s

sebességgel indult. Ez számára az ütközéskor

u_{1}

, így (1) szerint az ütközés előtti sebessége

v_{1} = 4 u_{1} = 4 m/s

volt. Eredeti helyéről (3) szerint

\sqrt[]{4^{2} + 1} m/s = \sqrt[]{17} m/s = 4, 12 m/s

-mal kellett indulnia.

2. Téglatest alakú víztartály kis kerekeken gurul (2. ábra). A tartály hossza

20 cm

, magassága

10 cm

, szélessége

10 cm

. Benne a víz magassága

9 cm

. A kocsi tömege vízzel együtt

2 kg

. Hogyan mozog a kocsi, ha a csigáról lelógó fonálon

1, 2 kg

tömegű test lóg? A súrlódás elhanyagolható.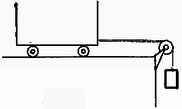

2. ábra

Megoldás. Kezdetben a kocsiban

2 dm \cdot 1 dm \cdot 0, 9 dm = 1, 8 {dm}^{3}

víz van, amelynek tömege

1, 8

kg. A kocsi szerkezetének tömegére

0, 2

kg marad.
A szokásos kocsikísérletnél

m_{1}

tömegű kocsit

m_{2}

lelógó tömeg súlya egyenletesen gyorsuló mozgással mozgat, amelynek gyorsulása:

\begin{matrix} a = \frac{m_{2}}{m_{1} + m_{2}} \cdot g . \end{matrix}

(4)

A mi esetünkben

a = 1, 2 g / (2 + 1, 2) = 3 g / 8

volna a gyorsulás.
Ha a kocsi: a benne levő vízzel állandó gyorsulással mozog, akkor a víz felszíne nem marad vízszintes, hanem elferdül, hajlásszöge a vízszinteshez képest

α

lesz, és erre az

α

-ra nézve igaz, hogy (3. ábra):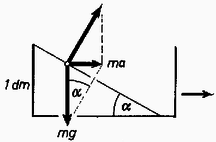

\begin{matrix} tg α = \frac{a}{g} . \end{matrix}

3. ábra

Biztosan kicsurog a víz egy része, ezzel megváltozik a kocsi teljes tömege

α

hajlásszögű vízfelszín esetében a megmaradt víz térfogata:

\begin{matrix} \frac{1}{2} \cdot \frac{1 dm}{tg α} \cdot 1 dm \cdot 1 dm = \frac{1}{2 tg α} liter, \end{matrix}

tömege

1 / (2 tg α)

kg. A kocsikísérletre érvényes (4) törvényben

m_{2} = 1, 2

kg,

m_{1} = [0, 2 + 1 / (2 tg α)]

kg,

a / g = tg α

, tehát:

\begin{matrix} tg α = \frac{1, 2}{0, 2 + 1 / (2 tg α) + 1, 2} . \end{matrix}

Az egyenlet megoldása

tg α = 0, 5, a = g / 2

. Ezzel a gyorsulással mozog a kocsi. Éppen 1 liter víz maradt benne, így kicsordult

0, 8

liter. A víz éppen a kocsi jobb oldali sarkáig ér. Ha

tg α

-ra

0, 5

-nél kisebb értéket kaptunk volna, ez azt jelentené, hogy a víz trapéz keresztmetszetű hasáb alakjában tölti meg a kocsit, és ekkor eszerint kellett volna a megmaradt víz térfogatát számítani. Mivel feladatunk adatai szerint a kettő közötti határesetről van szó, ezért a térfogat mindegyik számítási módja ugyanarra a helyes eredményre vezet.
Megvizsgálható, hogy a kocsi mozgásállapota stabilis, ami azt jelenti, hogy még több víz kicsurgása mellett egy új, maradandó gyorsulás áll be, a mozgás nem gyorsul fel határtalanul.

3. Lassan körfolyamatot hajtunk végre

2 gramm 0^{\circ} C

hőmérséklet,

1

atmoszféra nyomású,

22, 4 liter

térfogatú hidrogéngázzal. Először állandó térfogaton melegítjük, amíg nyomása

2

atmoszféra lesz. Azután állandó nyomáson melegítjük

546^{\circ} C

hőmérsékletig. Végül a

p V

-diagramban egyenes vonal mentén visszajuttatjuk eredeti állapotába. A hidrogén fajhője állandó térfogaton

2, 4 {cal/gr}^{\circ}

C, állandó nyomáson

3, 4 {cal/gr}^{\circ}

C. a) Mennyi ennek a folyamatnak a hatásfoka? b) Hogyan kell a körfolyamat alkalmával a hőmérsékletet változtatni a térfogat, illetve a nyomás függvényében?

Megoldás. Felrajzoljuk az 1 mól hidrogéngáz 273 K, 546 K és 819 K hőmérséklethez tartozó izotermáit (4. ábra).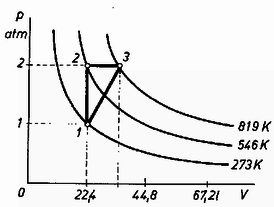

4. ábra

A körfolyamat az 1 ponttal jellemzett helyről indul el. 2-be érve a kétszeres nyomáshoz 2-szeres hőmérséklet, 546 K tartozik; a közben felvett hő

2, 4 \cdot 2 \cdot 273 cal = 1310 cal

. 819 K-re melegítve a hőmérséklet

1, 5

-szeres, tehát a térfogat is

1, 5 \cdot 22, 4 = 33, 6

lesz (3 pont); közben a felvett hő

3, 4 \cdot 2 \cdot 273 cal = 1856 cal

. A hidrogén összesen

1310 + 1856 = 3166 cal

-t vett fel. A harmadik lépésben, 3-ból 1-be haladva azután bizonyos kalórialeadás megy végbe.
A hatásfokot a munkavégzés és a felvett hőmennyiség hányadosa adja meg. A munkavégzést a diagram által bezárt terület jelenti:

W = \frac{1}{2} \cdot 1 atm \cdot 11, 2 liter = 5, 6 lit \cdot atm = 560 joule = 134 cal

.

A hatásfok

134 : 3166 = 0, 042 = 4, 2 %

.
Az 1 és 3 pontokon átmenő egyenes egyenlete:

\begin{matrix} \frac{p - p_{1}}{V - V_{1}} = \frac{p_{3} - p_{1}}{V_{3} - V_{1}} . \end{matrix}

Rendezve:

\begin{matrix} p = \frac{p_{3} - p_{1}}{V_{3} - V_{1}} \cdot V + \frac{p_{1} V_{3} - p_{3} V_{1}}{V_{3} - V_{1}} . \end{matrix}

A gáztörvény alapján

V

helyébe

T

hőmérsékletet hozzuk be,

V = R T / p

, ekkor a függvény:

\begin{matrix} T = \frac{1}{R} \cdot \frac{p_{3} - p_{1}}{V_{3} - V_{1}} \cdot V^{2} + \frac{1}{R} \cdot \frac{p_{1} V_{3} - p_{3} V_{1}}{V_{3} - V_{1}} \cdot V . \end{matrix}

Tehát az 1‐3 úton a hőmérsékletet a térfogat négyzetes függvénye szerint kell változtatnunk. Ugyanilyen függvényt kapunk, ha a nyomást használjuk független változónak. Az 1‐2 és a 2‐3 változások közben a hőmérsékletet természetesen a nyomással, illetve a térfogattal arányban kell változtatnunk.

A II. forduló feladatai:

1. Egy űrhajós először

r_{1}

sugarú körpályán

T_{1}

keringési idővel keringett a Föld körül. Űrhajójának kétszeri pályamódosításával pontosan

2 r_{1}

sugarú körpályára tért át. Az első módosításnál csak a sebességének a nagyságát változtatta, irányát nem. A második pályamódosítást ezután a legelső alkalmas pillanatban hajtotta végre, ekkor viszont sebességének csak az irányát változtatta, a nagyságát nem. a) Hány százalékkal növelte mozgási energiáját az első módosításkor? b) Mekkora szöggel kellett megváltoztatnia a sebességet a második alkalommal? c) Mennyi idő telt el a két pályamódosítás közölt? (Feltesszük, hogy a sebességváltoztatások a keringési időhöz képest igen gyorsan történtek.)

(Bodó Zalán)

Megoldás. Ha

m

tömeg

r

sugarú pályán kering az igen nagy

M

tömeg körül, akkor a centripetális és gravitációs erő egyenlő:

m v^{2} / r = f M m / r^{2}

. Innen a körsebesség és a mozgási energia a körpályán:

\begin{matrix} v = \sqrt[]{\frac{f M}{r}}, \frac{m v^{2}}{2} = \frac{f M m}{2 r}, \end{matrix}

(5)

(

f

a gravitációs állandó).
A keringő űrhajó összes energiája mozgási és helyzeti energiájának összegével egyenlő. Ha az űrhajó

A F = r_{1}

sugarú körpályán kering, akkor mozgási energiája (5) szerint

f M m / 2 r_{1}

. A helyzeti energiát az

A

pontban meglevő helyzeti energiához viszonyítjuk, itt 0-nak számítjuk (5. ábra). Így az összes energia az

r_{1}

sugarú körpályán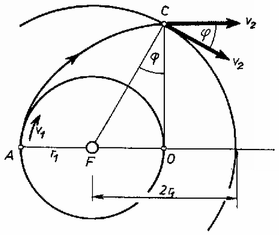

f M m / 2 r_{1}

5. ábra

2 r_{1}

sugarú körpályán a mozgási energia (5)szerint

f M m / 4 r_{1}

. A helyzeti energia:

\begin{matrix} \int_{r_{1}}^{2 r_{1}} \frac{f M m}{r^{2}} \cdot d r = f M m (\frac{1}{r_{1}} - \frac{1}{2 r_{1}}) = \frac{f M m}{2 r_{1}} . \end{matrix}

Tehát a

2 r_{1}

sugarú körpályán az összes energia:

f M m / 4 r_{1} + f M m / 2 r_{1} = 3 f M m / 4 r_{1}

. Látható, hogy az összes energiát

1 / 2 : 3 / 4

arányban, tehát 50%-kal kell növelni.
Tehát az első pályamódosításkor

A

-ban 50%-kal kell növelni a mozgási energiát. Ezután az ellipszispályán mindvégig ugyanennyi marad az összes energia.

C

pontban csak irányváltozás történik, ezért az összes energiában nincs változás a második pályamódosításkor és ez ugyanennyi marad a külső körpályán is, mint az átmeneti ellipszisen.
A mechanika törvényei, a Kepler-törvények szerint a keringő bolygó összes energiája csak a fél nagytengelytől függ. Mivel az átmeneti ellipszisen és a külső körön ugyanannyi az összes energia, a fél nagytengelynek is egyenlőnek kell lennie a két esetben. Ez a külső körnél

2 r_{1}

, tehát ennyi az ellipszis fél nagytengelye is. Ha az

A

csúcsból felmérjük a

2 r_{1}

távolságot, akkor az átmeneti ellipszis centrumába jutunk. Ez

O

-ban van, a kis kör másik oldalán. Minthogy

F C = 2 r_{1}

C O

az átmeneti ellipszis fél kistengelye. A második pályamódosításnak az átmeneti ellipszis kistengelyének végpontjában kell történnie.

F C O ∢ = 30^{\circ} = φ

. Ekkora szöggel kell megváltoztatni a sebesség irányát. Közben az űrhajó energiája változatlan marad, a hajtómű energiakifejtését teljes egészében az égéstermékek kapják meg.
Az átmeneti ellipszisen

A

és

C

között eltelt időt Kepler második törvényével kapjuk meg. Ha az átmeneti ellipszisen a keringési idő

T_{2}

, akkor a területi sebesség

π a b / T_{2}

. A vezérsugár által leírt terület a negyedellipszis és a háromszög területének különbsége:

π a b / 4 - a b / 4 = a b (π - 1) / 4

. A keresett időt a terület és a területi sebesség hányadosa adja meg:

\begin{matrix} \frac{a b (π - 1)}{4} : \frac{π a b}{T_{2}} = \frac{π - 1}{4 π} \cdot T_{2} \approx 0, 17 T_{2} . \end{matrix}

Kepler harmadik törvénye alapján a második körön (ill. ellipszisen) érvényes keringési idő kifejezhető az első körön szereplő keringési idővel:

T_{2} = T_{1} \cdot 2 \sqrt[]{2}

2. Az optikai tengelyen 4‐4 dm-es távolságban következnek egymás után:

T

pontszerű fényforrás,

- 4 dm

gyújtótávolságú szórólencse,

+ 4 dm

gyújtótávolságú gyűjtőlencse és

8 dm

gyújtótávolságú homorú gömbtükör. Mindegyikük átmérője

d = 2 dm

(6. ábra). A pontszerű fényforrást kimozdítjuk az optikai tengelyből. Mennyi lehet a merőleges

x

távolság, hogy módunkban legyen a tükör által adott képet ernyőn felfogni?

(Bodó Zalán)

6. ábra

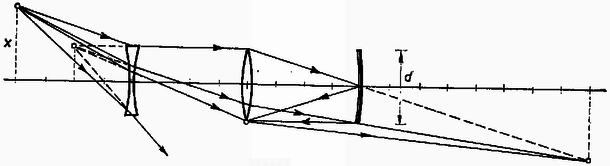Megoldás. A szórólencse által adott virtuális kép képtávolsága

- 4 \cdot 4 / (4 + 4) = - 2

dm, a kép mérete

x / 2

. Ez a virtuális kép a gyűjtőlencse számára 6 dm távolságban levő tárgy, amelyről

6 \cdot 4 dm / (6 - 4) = 12

dm távolságban keletkezik kétszeresen nagyított, tehát ismét

x

nagyságú reális kép. A homorú gömbtükör számára ez

- 8

dm távolságban álló virtuális tárgy, amelyről

- 8 \cdot 8 / (- 8 - 8) = 4

dm távolságban reális kép keletkezik felére kicsinyítve, tehát

x / 2

méretben.
A végső reális kép éppen a gyűjtőlencse síkjában jön létre, ernyőn való felfogását a lencse akadályozza. Amint az

x

távolságot növeljük, a képpont is vándorol kifelé. A kép akkor kerül a lencse mellé, ha

x

nagyobb lesz, mint

d

, így a kép felfoghatóságának egyik feltétele, hogy

d < x

legyen. Ha

x

eléri az

1, 5 d

értéket, akkor a sugárnyaláb lecsúszik a homorú gömbtükörről és nem kapunk képet. Tehát a feladat megoldása:

\begin{matrix} d < x < 1, 5 d . \end{matrix}

U

elektromotoros erejű és

r

belső ellenállású galvánelemekből összeállítjuk a 7. ábra szerinti végtelen láncot. Mennyi az elektromotoros erő és a belső ellenállás az A és B pont között?

(Vermes Miklós)

7. ábra

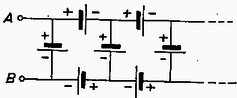Megoldás. A végtelen ellenállásláncra közismert ez az eredmény:

(\sqrt[]{3} - 1) r

. (L. például az 1957. évi középiskolai tanulmányi verseny II. fordulójának 3. feladatát.) A mi feladatunkban ennyi az elemlánc belső ellenállása.
Vizsgáljunk meg két különböző, párhuzamosan kapcsolt elemet (8. ábra).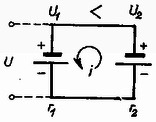

8. ábra

Ezek eredő elektromotoros erejének azt az

U

feszültséget fogjuk nevezni, amelyet külső terhelő ellenállás nélkül mérhetünk a pólusokon, (bár az elemek belsejében ilyenkor folyik

i

erősségű áram). Az elem belsejében fellépő feszültségeséseket figyelembe véve:

\begin{matrix} U & = U_{2} - i r_{2}, \\ U & = U_{1} + i r_{1} . \end{matrix}

Ennek megoldásával az ilyen módon meghatározott elektromotoros erő:

\begin{matrix} U = \frac{U_{1} r_{2} + U_{2} r_{1}}{r_{1} + r_{2}} \end{matrix}

(6)

Most foglalkozunk az elemlánccal (9. ábra).

9. ábra

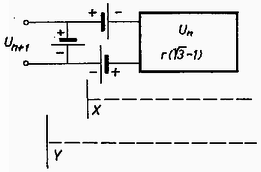Egy igen hosszú részének az elektromotoros ereje legyen

U_{n}

belső ellenállása az előbb idézett eredmény szerint

r (\sqrt[]{3} - 1)

. Először hozzákapcsolunk sorba két elemet, ábránkon

X

-ig haladva. Most az elektromotoros erő

U_{2} = 2 U + U_{n}

, a belső ellenállás

r_{2} = 2 r + r (\sqrt[]{3} - 1) = r (\sqrt[]{3} + 1)

. Ezután az

X

-ig tartó részhez hozzákapcsolunk még egy elemet

U = U_{1}

elektromotoros erővel és

r = r_{1}

belső ellenállással, a 9. ábrán

Y

-ig haladva. A párhuzamos elemek (6) szerinti törvénye alapján az elektromotoros erő:

\begin{matrix} U_{n + 1} = \frac{U r (\sqrt[]{3} + 1) + (2 U + U_{n}) r}{r + r (\sqrt[]{3} + 1)} = \frac{u (\sqrt[]{3} + 3) + U_{n}}{\sqrt[]{3} + 2} . \end{matrix}

A végtelen hosszú láncra az jellemző, hogy egy tag hozzácsatolása már alig változtat az eredményen.

U_{n + 1} = U_{n}

helyettesítés után:

\begin{matrix} U_{n} = \frac{U (3 + \sqrt[]{3}) + U_{n}}{\sqrt[]{3} + 2} . \end{matrix}

Az egyenlet megoldása adja az elemlánc eredő elektromotoros erejét:

\begin{matrix} U_{n} = \sqrt[]{3} \cdot U . \end{matrix}

Az 1972. évi fizika tanulmányi verseny eredménye

I. díj Imhof Gyula (Szekszárd, Garay J. Gimn. IV. o. t., Tanára: Póla Károlyné),
II. díj Gál Péter (Fazekas M. Gimn. IV. o. t., Tanára: Dr. Szalay Béla),
III. díj Éber Nándor (Budapest, Móricz Zs. Gimn., IV. o .t., Tanára: Kádár Lászlóné) és
Szabó Zoltán (Budapest, Apáczai Csere J. Gimn. IV. o. t. Tanára: Turtóczky Sándor).

A további helyezettek: 5. Gegus Gábor (Budapest, Móricz Zs. Gimn., IV. o. t., Tanára: Kádár Lászlóné); 6. Vassel Róbert (Budapest, I. István Gimn., IV. o. t., Tanára: Moór Ágnes); 7. Vermes András (Eger, Gárdonyi G. Gimn., IV. o. t., Tanára: Palotás József); 8. Pach János (Budapest, Veres Pálné Gimn., IV. o. t., Tanára: Kishonti Istvánné); 9. Tóth Tamás (Budapest, Jedlik Á. Gimn., IVI o. t., Tanára: Vermes Miklós); 10. Balog János (Budapest, I. István Gimn., IV. o. t.; Tanára: Moór Ágnes);