Kezdőlap


Cím:	1971. évi Eötvös Loránd Fizikaverseny
Füzet:	1972/február, 81 - 84. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat október 23-án rendezte ez évi fizikai versenyét. A versenyzők 5 óráig dolgozhattak és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását.

r

rádiuszú kerék kerületére vékony gumikarikát feszítünk, amelynek tömege

m

, eredeti hossza

L

és hosszegységgel való megnyújtásához

D

erő szükséges. A súrlódási együttható a kerék kerülete és a gumikarika között

μ

. A kereket nyugalomból kiindulva

β

állandó szöggyorsulással forgatjuk. Mekkora szögsebességnél csúszik meg a karika ? Mekkora szögsebességnél esik le ?

Megoldás. Ha a kerékre ráfeszítjük a gumikarikát, akkor hosszát megnöveltük

(2 π r - L)

darabbal, aminek következtében a gumiszalagban

(2 π r - L) D

rugalmas erő támad. Ez a rugalmas erő mindenütt az érintő mentén működik. Ki kell számítani, hogy

F_{t}

érintő mentén működő erő mekkora középpont felé irányuló, az érintőre merőleges

F_{n}

erőt hoz létre a kerület minden pontjában (1. ábra).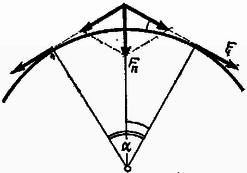

1. ábra

Ha a körív

α

középponti szöghöz tartozó darabját nézzük, akkor

F_{n} = 2 F_{t} sin (α / 2)

. Kis

α

szög esetében, a szöget mindig radiánban számítva

F_{n} = α F_{t}

.
Az előbb számított

(2 π r - L) D

rugalmas erőtől származó merőleges erő

(2 π r - L) D α

. A gumikarika

α

szöghöz tartozó darabját a kerülethez odaszorító erőt megkapjuk, ha kivonjuk belőle a centrifugális erőt. Az

α

középponti szöghöz tartozó karikarész tömege

α m / (2 π)

. Ezt szorozva

ω^{2} r

-rel kapjuk a centrifugális erőt :

α m ω^{2} r / (2 π)

. Végeredményben a vizsgált tömegrészt merőlegesen a kerékhez odaszorító erő :

\begin{matrix} (2 π r - L) D α - \frac{m ω^{2} r}{2 π} \cdot α . \end{matrix}

(1)

Ahhoz, hogy a gumikarika a kerék kerületével együtt

α = β r

gyorsulással gyorsuljon,

α m β r / 2 π

gyorsító erő szükséges az érintő irányában. A merőlegesen odaszorító erőből származó lehetséges legnagyobb súrlódási erőt megkapjuk, ha az (1) alatti erőt

μ

-vel szorozzuk. Mivel a súrlódás adja át a kerékről a karikának a gyorsító erőt, azért azt az

ω_{1}

szögsebességet, amely felett a karika megcsúszik, úgy kapjuk meg, hogy a maximálisan lehetséges súrlódási erőt egyenlővé tesszük a gyorsításhoz szükséges erővel :

\begin{matrix} μ [(2 π r - L) D α - \frac{m ω_{1}^{2} r}{2 π} \cdot α] = \frac{m β r α}{2 π} . \end{matrix}

Innen :

\begin{matrix} ω_{1} = \sqrt[]{\frac{2 π (2 π r - L) D}{m r} - \frac{β}{μ}} . \end{matrix}

Ezzel válaszoltunk az első kérdésre. Az ún. leesés feltétele, hogy az (1) alatti odaszorító erő eltűnjön. Ebből az egyenletből az ehhez szükséges

ω_{2}

\begin{matrix} ω_{2} = \sqrt[]{\frac{2 π (2 π r - L) D}{m r}} . \end{matrix}

Miközben a kerék szögsebessége állandó szöggyorsulással tovább növekszik,

ω_{1}

elérése után a gumikarika szögsebessége már kisebb, mint a keréké, és

ω_{2}

a gumikarika szöggyorsulásának felső határát jelenti, amelyet csak aszimptotikusan közelít meg.
Az adatok számértékei a versenyfeladatban a következők voltak :

r = 10 cm = 0, 1 m

;

m = 1, 256 kg

;

L = 0, 608 m

;

D = 0, 05 kp/cm = 50 newton/m

;

μ = 0, 02

;

β = 2 s^{- 2}

. Ezekkel az adatokkal a gumikarika már az indulás pillanatában megcsúszik, mert a rugalmas erő a centrifugális erő beszámítása nélkül sem tud akkora súrlódási erőt létrehozni, amely a kerékkel egyező gyorsulással gyorsítaná a karikát. A karika szögsebességének felső határértéke

ω_{2} = 7, 07 s^{- 1}

. Amennyiben a karika tömege

0, 1256 kg

, a megcsúszás szögsebessége

ω_{1} = 20 s^{- 1}

és

ω_{2} = 22, 4 s^{- 1}

L = 1 méter

hosszú, egyik végén beforrasztott vékony üvegcsőben

1 atmoszféra

nyomás mellett

h = 20 cm

hosszú higanyoszlop zár el

l_{0} = 20 cm

hosszú légoszlopot : A csövet zárt vége körül

ω = 6 s^{- 1}

szögsebességgel forgatjuk vízszintes síkban. Milyen hosszú most az elzárt légoszlop ?

Megoldás. Adott szögsebességgel történő forgás közben a légoszlop hossza

l

(2. ábr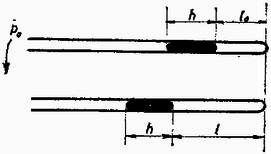a).

2. ábra

A külső légnyomás

p_{0}

. Forgás közben a légoszlop belsejében a nyomás Boyle‐Mariotte törvénye szerint

p = p_{0} l_{0} / l

. Számítani kell a higanyra ható centrifugális erőt. Felhasználva a higany

ϱ

sűrűségét, az egységnyi alapterületű higanyoszlop tömege

h ϱ

. Tekintettel arra, hogy

m ω^{2} r

centrifugális erő a középponttól mért távolsággal egyenes arányban növekszik, a higanytömegre ható centrifugális erőt úgy számíthatjuk, mintha a higany a forgástengelytől

l + h / 2

távolságban volna, és így a centrifugális erőből származó, kifelé vivő nyomás

h ϱ ω^{2} (l + h / 2)

. A higanyt kifelé vivő nyomások összege egyensúly esetében egyenlő

p_{0}

külső nyomással :

\begin{matrix} p_{0} = \frac{p_{0} l_{0}}{l} + h ϱ ω^{2} (l + \frac{h}{2}) . \end{matrix}

(2)

l

ismeretlenre rendezve :

\begin{matrix} l^{2} + (\frac{h}{2} - \frac{p_{0}}{h ϱ ω^{2}}) l + \frac{p_{0} l_{0}}{h ϱ ω^{2}} = 0. \end{matrix}

Ennek megoldása :

\begin{matrix} l = \frac{1}{2} \cdot [\frac{p_{0}}{h ϱ ω^{2}} - \frac{h}{2} \pm \sqrt[]{{(\frac{p_{0}}{h ϱ ω^{2}} - \frac{h}{2})}^{2} - \frac{4 p_{0} l_{0}}{h ϱ ω^{2}}}] . \end{matrix}

Feladatunk számadatait célszerűen ilyen alakban használjuk :

p_{0} = 10 {newton/cm}^{2} = 10^{5} {newton/m}^{2}

;

l_{0} = 0, 2 m

;

h = 0, 2 m

;

ϱ = 13, 6 {gramm/cm}^{3} = 1, 36 \cdot 10^{4} {kg/m}^{3}

;

ω = 6 s^{- 1}

. Így

p_{0} / h ϱ ω^{2} = 1, 021

méter, és az egyenlet két megoldása :

l_{1} = 37, 2 cm

l_{2} = 54, 9 cm

. Mindegyik esetben a higany az 1 méter hosszú esőben marad.
Meg kell vizsgálnunk a feladat eredményeként adódó két egyensúlyi helyzet minőségét. Grafikusan ábrázoljuk a légoszlop

l

hosszának függvényében a higanyt kifelé vivő nyomást, amelyet (2) jobb oldala ad meg (3. ábra).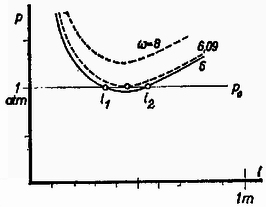

3. ábra

Minimumot végigfutó görbét kapunk. Ennek a

p_{0} = 1

atmoszféra magasságban húzott egyenessel alkotott metszéspontjai mutatják a feladat

l_{1}

és

l_{2}

megoldásait. Azonnal kiderül, hogy ha a higany kifelé csúszna, akkor ezzel

l_{1}

-nél a befelé vivő,

l_{2}

-nél a kifelé vivő nyomás válna nagyobbá. Tehát

l_{1}

stabilis,

l_{2}

labilis egyensúlyi helyzetet jelent. A higany befelé való elmozdulásából is ugyanez következik.
Amennyiben

ω

szögsebesség nagyobb, a kifelé vivő nyomást ábrázoló görbe feljebb tolódik.

ω = 6, 09 s^{- 1}

szögsebességnél a megoldás képletében a diszkrimináns nulla lesz, a görbe érinti az 1 atmoszféra magasságában húzódó egyenest, és egyetlen egyensúlyi helyzet adódik, amely labilis. Még nagyobb szögsebességnél semmiféle egyensúlyi helyzet sem lehetséges.

3. Nagy kiterjedésű, sík, földelt fémlap fölött a 4. ábrán látható módon elhanyagolható súlyú, szigetelő fonálon rögzítve egyenlő tömegű, szigetelő anyagból készült kis golyók függenek. A golyók mindegyikének ugyanakkora, egyenletesen elosztott pozitív elektromos töltése van. Megváltozik-e a golyósor alakja, ha a fémlapra pozitív elektromos feszültséget kapcsolunk ?
(Károlyházi Frigyes)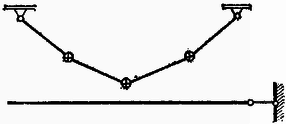

4. ábra

Megoldás. Először is azt kell belátnunk, hogy már a földelt fémlap esetében sem olyan a golyósor alakja, mint amikor a fémlap nincs ott. Tegyük fel, hogy először csak a golyósor van jelen, a potenciálok vonatkoztatási pontja, a Föld valahol nagyon messze van. A golyósor alakját az 5. ábrán az 1. számú pontozott vonal tünteti fel. Amennyiben a golyók súlya egyenlő, mindig ez az alak jön létre.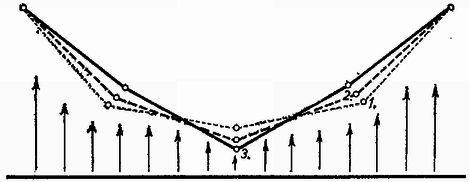

5. ábra

Ezután helyezzük el az igen nagy kiterjedésű fémlapot. A megosztás folytán a lapban mutatkozó negatív töltések lefelé húzzák a golyókat, de a középső golyót erősebben, mert közelebb van a lemezhez. (A vonzóerők egyébként úgy számíthatók, mintha a megosztott töltések az eredetieknek a tükörképei volnának.) Mivel a megosztott töltések a középső golyót nagyobb erővel vonzzák, mint a szélsőket, a golyósor középen kihegyesedik, a középső golyó lejjebb húzódik (2. számú, szaggatott vonal). Ne felejtsük el, ez a kihegyesedés annál nagyobb mértékű, minél k ö n n y e b b e k a golyók. Ebben az állapotban kezdődik a feladat szövege.
Ha a fémlapot pozitív feszültségre kapcsoljuk, akkor környezetében homogén elektromos tér jön létre. Ha a lap elég nagy kiterjedésű, akkor ez a tér gyakorlatilag homogén, és így mindegyik golyót ugyanakkora erővel taszítja. Ez a taszítás olyan, mintha a golyók könnyebbekké váltak volna. De előbbi meggondolások szerint a középen nagyobb, a széleken kisebb elektromos erő, amelyet a most is működő megosztás jelent, k ö n n y e b b golyóknál n a g y o b b hegyesedést okoz. Így pozitív feszültség esetében a pozitív töltésű középső golyó lejjebb húzódik a 3. számú folytonos vonal szerint.

A verseny eredménye: I. díjat nyert Nagy András honvéd (a budapesti Fazekas Gimnáziumban Hutay Ferenc volt tanítványa). A II. díj nem került kiosztásra. III. díjat nyert Szabó Zoltán, a budapesti Apáczai Csere Gimnázium IV. osztályos tanulója (tanára Turtóczky Sándor). Dicséretet kaptak és könyvjutalomban részesültek Balog János, a budapesti I. István Gimnázium IV. osztályos tanulója (tanára Moór Ágnes), Horváth László, a hódmezővásárhelyi Bethlen Gábor Gimnázium IV. osztályos tanulója (tanára Horváth István és Bodrogi Sándor), Kövér András, a debreceni Kossuth Lajos imnázium IV. osztályos tanulója (tanára Czirjék Lászlóné), Monostori László, a budapesti Műszaki Egyetem villamosmérnök hallgatója (a budapesti Fazekas Gimnáziumban Hutay Ferenc volt tanítványa), és Vassel Róbert, a budapesti I. István Gimnázium IV. osztályos tanulója (tanára Moór Ágnes).