Cím: "Mohr ""Euclides Danicus""-a"
Szerző(k):  Strommer Gyula 
Füzet: 1972/november, 103 - 108. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mohr "Euclides Danicus''-a
 

A geometriai szerkesztések segédeszköze a vonalzó és a körző. A vonalzót két adott ponton átmenő egyenes húzására, a körzőt adott pont körül két adott pont távolságával egyenlő sugarú kör rajzolására használjuk. Szerkesztett pontoknak csak azokat a pontokat tekintjük, amelyeket az ilyen módon megrajzolt egyenesek és körök metszéspontjai szolgáltatnak. A már szerkesztett pontokat a további szerkesztésekben adottnak vesszük.
A körzővel és vonalzóval elvégezhető szerkesztések tehát a következő háromféle alapszerkesztésből tehetők össze: 1. két egyenes, 2. egyenes és kör és 3. két kör metszéspontjainak szerkesztéséből.
A XVIII. század végén Mascheroni1 megmutatta, hogy az összes mértani szerkesztések csupán körzővel is elvégezhetők.2 Mascheroni érdekes fölfedezését "La geometria del compasso'' című munkájában 1797-ben Páviában közölte. E dolgozat annak idején nagy feltűnést keltett és szerzője nevét a tudomány történetében emlékezetessé tette.
Csak sokkal később szerzett arról tudomást a matematikus világ, hogy G. Mohr dán matematikus már 125 évvel Mascheroni előtt ugyanerre az eredményre jutott "Euclides Danicus'' című művében.
 
 

Georg Mohr, vagy valódi nevén Mohrendal (Mohrenthal), 1640. április 1-én Koppenhágában született, hol atyja kereskedő volt és a kórház felügyelője. Ifjú korától fogva a matematika felé vonzódott. Mint 22 éves fiatal ember Angliába, Franciaországba és Hollandiába ment a matematikában alapos ismeretekre szert tenni, mely alkalommal számos tudóssal, pl. Leibnizcel és Tschirnhausszal 3 is megismerkedett. Hosszabb ideig tartó távollét után hazájába visszatérvén, csakis tudományos kutatásainak élt. 1687-ben Hollandiába tette át tartózkodása helyét. Végül 1695-ben barátjának, Tschirnhausnak unszolására Kieslingswaldeba költözött át, hogy tudományos tevékenységében segítségére legyen, ahol 1697. január 26-án meg is halt.
Mohr több művet írt, de kéziratai 1672-ben az akkori háborúkban nagyrészt elvesztek. Egyetlen műve maradt ránk, s ez a már fönt említett "Euclides Danicus'', mely éppen 300 évvel ezelőtt, 1672-ben jelent meg Amsterdamban dán és holland nyelven, anélkül azonban, hogy figyelmet keltett volna, mert az értekezés címe nem volt a legszerencsésebben választott, s emiatt azt hitték, hogy Euklides "Elemek'' című művének kivonata vagy fordítása. A munka, bár puszta címe Murhard "Bibliotheca mathematica'' (Lips. 1797‐1805) című könyvészeti műve II. kötetében (a 36‐37. lapon) a holland Euklides‐fordítások között megtalálható, a tudományos irodalomban teljesen ismeretlen maradt. Csak 1928-ban terelődött rá a közfigyelem, midőn V. Beck, akkoriban egyetemi hallgató, egy koppenhágai könyvárusnál megtalálta a mű egy holland nyelvű példányát; Johannes Hjelmslev koppenhágai egyetemi tanár pedig, kinek a könyvet Beck megmutatta s ki azt nagy érdeklődéssel áttanulmányozta, ismertetést írt róla.
 

Mohr műve a koppenhágai akadémia kiadásában 1928-ban Koppenhágában újra megjelent eredeti dán nyelven, melyhez hazánkfia, Pál Gyula német fordítását csatolták.
A szóban forgó munka első részében a szerző az Euklides‐féle "Elemek'' első hat könyvében előforduló összes szerkesztési feladatot csupán körzővel oldja meg; a második és egyszersmind utolsó részben a pusztán körző segitségével végrehajtott szerkesztések különféle alkalmazásait tárgyalja.
A következőkben ismertetni óhajtjuk a Mohr‐féle szerkesztések közül azokat, amelyek segítségével a geometria összes szerkesztési feladatai megoldhatók. A feladatok a következők:
 

1. feladat. Határozzuk meg valamely AO távolság kétszeresét.
 

Megoldás: O körül AO sugárral kört rajzolunk, melynek kerületére az A pontból kiindulva háromszor rámérjük az AO sugarat mint húrt; az utolsó osztási pont a körnek A-val átellenes D pontja. Emiatt A, O és D egy egyenesben feküsznek és
AD=2⋅AO.

Ezen eljárás többszöri alkalmazásával szerkeszthetünk olyan N pontot hogy
AN=n⋅AB,
ahol n egész számot jelent.
 

2. feladat. Osszuk az adott kör kerületét négy egyenlő részre.
 

Megoldás: A kör tetszés szerinti A pontjából kiindulva az AO sugarat háromszor rámérjük úgy, hogy AB=BC=CD=OA-val.
Ezután A és D pontokból mint középpontokból AC=BD sugárral köríveket rajzolunk; ezek metszéspontját E-vel jelöljük.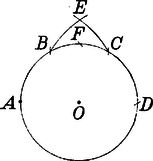
 
 

Ha most A pontból OE sugárral az adott kört F-ben átmetsszük, akkor AF a körbe írt szabályos négyszögnek egyik oldala lesz.
 

Bizonyítás: Minthogy az ACD derékszögű háromszögben AD=2⋅CD, azért
AC2¯=3⋅CD2¯,
amiből következik, hogy az AOE derékszögű háromszögben
OE2¯=2⋅AO2¯,
vagyis OE a 90∘-ú húrnak a hossza.
 

3. feladat. Adva van két távolság AB és CD oly módon, hogy AB=2⋅CD; felezzük az AB távolságot.
 

Megoldás: C pontból CD távolsággal félkört írunk le, melyre a sugarat háromszor rámérjük, úgy, hogy 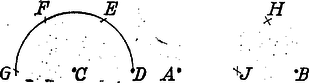DE=EF=FG=CD.
 

 

Most A-ból GE körzőnyílással körívet rajzolunk és azt H-ban olyan körívvel metsszük át, melynek sugara DE, középpontja pedig B. Végre B-ből és H-ból CD körzőnyílással egymást metsző köríveket rajzolunk. Ha az így nyert pontok közül J azon pont, melynek A-tól való távolsága CD-vel egyenlő, akkor J az AB távolság felezőpontja.
 

4. feladat. Felezzük az AB távolságot.
 

Megoldás: Mindenekelőtt meghatározzuk a C és D pontokat úgy, hogy azok AB-vel egy egyenesbe essenek és CA=AB=BD legyen. Azután rajzoljunk C és D pontokból BC=AD távolsággal köríveket; ezek metszéspontját E-vel jelöljük.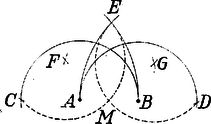
 

 

Most a CE és DE távolságot az előbb bemutatott szerkesztés szerint F-ben és G-ben felezzük. Ha végre F-ből és G-ből E ponton át köríveket rajzolunk, melyek egymást még M pontban metszik, akkor M-ben a keresett felezőpontot nyerjük.
 

5. feladat. Ejtsünk valamely AB egyenesre kívüle fekvő C pontból merőleges egyenest és határozzuk meg ennek M talppontját.
 

Megoldás: A-ból és B-ből C ponton át köríveket rajzolunk, melyek még D-ben metszik egymást. Ha most a 4. feladat szerint felezzük a CD távolságot M-ben, akkor az M pont a C pontnál AB-re ejtett merőleges talppontja.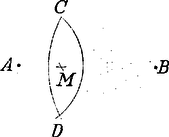
 

 

6. feladat. Emeljünk valamely AB egyenesre ennek A pontjában adott nagyságú AC merőlegest.
 

Megoldás: AB fölé a 4. alapján félkört rajzolunk és A-ból az adott távolsággal körívet írunk le, mely a félkört D-ben metszi (föltéve, hogy az adott távolság kisebb AB-nél). Ezután a 2. alapján felezzük a félkört E pontba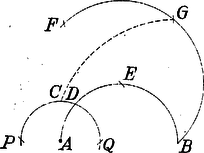n.
 

 

Most E-ből mint középpontból BE sugárral körívet írunk le és meghatározzuk a B-vel átellenes F pontot. Ezek megtörténte után F pontból BD sugárral a BF fölé rajzolt félkört G-ben átmetsszük.
Ha végre B-ből BG sugárral az adott távolsággal A-ból rajzolt körívet C-ben átmetsszük, akkor AC a keresett merőleges.
Bizonyítás: Az ABD derékszögű háromszögben
BD2¯=AB2¯-AD2¯,
az ABE egyenlő szárú derékszögű háromszögben
2⋅BE2¯=AB2¯,
és a BFG derékszögű háromszögben
BG2¯=BF2¯-BG2¯.

Csakhogy BF=2⋅BE és FG=BD, tehát
BG2¯=AB2¯+AD2¯.
De az ABC háromszögben BC=BG és AC=AD, amiből következik, hogy AC az AB-vel derékszöget képez.
Megjegyezzük, hogy ha az adott távolság nem volna kisebb AB-nél, vagyis nem lehetne az AB fölé rajzolt félkörre rávinni, akkor az AB távolság kétszeresét, háromszorosát, ..., n-szeresét kell venni és a félkört e fölé kell rajzolni, hogy célt érjünk.
 

7. feladat. Az A és B pontjaival megadott egyenesre vigyük fel A-tól a megadott MN távolságot.
 

Megoldás: Mindenekelőtt meghatározzuk az előbb bemutatott szerkesztés segítségével a C pontot úgy, hogy AC az AB egyenesre merőlegesen álljon és MN-nel egyenlő legyen. Azután meghatározzuk a 2. feladat szerint az A-ból AC sugárral leírt körön a P és Q pontokat úgy, hogy azok AB-vel egy egyenesbe essenek. Akkor AP=AQ=MN.
 

8. feladat. Keressük három távolsághoz a negyedik arányost.
 

Megoldás: Legyenek az adott távolságok AB, CD, EF és keressük azt az MN távolságot, melyre nézve
AB:CD=EF:MN.

Az általánosság rovása nélkül feltehetjük, hogy
AB>EF,
mert AB<EF esetében mindig vehetünk olyan n egész számot, hogy n⋅AB nagyobb legyen EF-nél, és akkor n⋅AB-, n⋅CD- és EF-hez keressük a negyedik arányost.
A szerkesztés menete a következő:
Az AB egyenesen meghatározzuk a G pontot úgy, hogy AG=CD legyen. Ezután AB fölé félkört rajzolunk és A-ból EF sugárral H-ban átmetsszük. Végre meghatározzuk a G pontból AH-ra ejtett merőleges egyenes J talppontját. Akkor AJ távolság a keresett negyedik arányos lesz.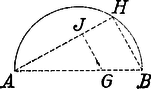
 

 

9. feladat. Keressük az A és B, illetőleg a C és D pontok által adott egyenesek metszéspontját.
 

Megoldás: Jelöljük a C és D pontokból AB-re bocsátott merőleges egyenesek talppontját E-vel és F-fel, és messe a 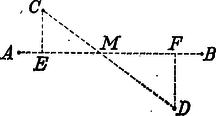CD egyenes AB-t az M-ben.
 

 

Ha C és D az AB egyenes különböző oldalain fekszenek, akkor
(CE+DF):CE=EF:EM.
Ha pedig a C és D pont az AB egyenes ugyanazon oldalára esik, akkor
(CE-DF):CE=EF:EM.

Ám CE, DF, EF ismertek, és így EM a 7. és 8. feladat alapján megszerkeszthető. Ha már most EM-et ismerjük, akkor az M pont helyzetét nyerjük, ha E-től az AB-re rávisszük az EM távolságot.
 

10. feladat. Határozzuk meg az A és B pontjaival megadott egyenes metszéspontjait az O középpontú és OC sugarú körrel.
 

Megoldás: a) O az AB egyenesen kívül van. A-ból és B-ből AO, ill. BO sugárral köríveket rajzolunk, melyek még P-ben metszik egymást. Most P-ből mint középpontból OC sugárral kört rajzolunk. A két kör M és N metszéspontjai az adott kör és az AB egyenes metszéspontjai.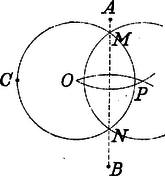
 

 

b) O az AB egyenesen van. Ez esetben meghatározzuk az AB egyenesen az M és N pontokat úgy, hogy OM=ON=OC legyen.
Látjuk tehát, hogy az 1. és 2. alapszerkesztés mindig visszavezethető a 3.-ra, mely körzővel közvetlenül elvégezhető. Ebből azonban következik, hogy minden körzővel és vonalzóval elvégezhető szerkesztés csupán körzővel is elvégezhető.
1Lorenzo Mascheroni, 1750. május 14-én született Bergamo mellett Castagnettoban, meghalt 1800. július 30-án Párizsban; szerzetes volt és a bergamoi líceumon, később a páviai egyetemen matematikát tanított.

2Megjegyezzük, hogy az olyan feladatokat, amelyek egyenesek húzását kívánják, megoldottnak tekintjük, ha két pontját meg tudjuk az egyenesnek szerkeszteni.

3Ehrenfried Walther von Tschirnhaus gróf 1651. április 10-én született Görlitz mellett Kieslingswaldeban, meghalt 1708. október 11-én Drezdában. Az optikai műszerek javításával foglalkozott; vörösrézből óriási gyújtótükröt készített, mely a drezdai "matematikai szalon''-ban még ma is látható.