Kezdőlap


Cím:	Gauss-féle binomiális együtthatók, I. rész (fordította Surányi János)
Szerző(k):	Pólya György
Füzet:	1972/november, 97 - 102. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Gauss-féle binomiális együtthatók¹

I. rész

A binomiális együtthatók szerepelnek a középiskolai tantervben, kapcsolatuk a kombinatorikával Leibniz, Pascal és Jacob Bernoulli kora óta jól ismert. Az ún. "Gauss‐féle binomiális együtthatók'' sokkal kevésbé közismertek, kapcsolatuk a kombinatorikával pedig új keletű. Ezért a Gauss‐féle és a közönséges binomiális együtthatók néhány kapcsolatának megvilágítása bizonyára új színt ad egy hagyományos középiskolai anyagrésznek.

1. Definíció: Gauss‐féle binomiális együtthatónak nevezzük az

\begin{matrix} [\binom{n}{r}] = \frac{(q^{n} - 1) (q^{n - 1} - 1) \cdot ... \cdot (q^{n - r + 1} - 1)}{(q - 1) (q^{2} - 1) \cdot ... \cdot (q^{r} - 1)} \end{matrix}

(1.1)

kifejezést, ahol

n

és

r

0 < r ≦ n

feltételt kielégítő egészek,

q

változó, amely minden 1-től különböző értéket felvehet;² a definíciót kiegészítjük az

r = 0

esetre és megemlítjük az

r = n

speciális esetet:

\begin{matrix} [\binom{n}{0}] = 1, [\binom{n}{n}] = 1. \end{matrix}

(1.2)

q = 1

esetet ki kellett zárnunk, mert a nevező minden tényezője osztható

q - 1

-gyel, de a számlálóé is. Ha viszont ezekkel a tényezőkkel egyszerűsítünk, azt kapjuk, hogy

\begin{matrix} [\binom{n}{r}] = \frac{(q^{n - 1} + q^{n - 2} + ... + q + 1) (q^{n - 2} + ... + 1) \cdot ... \cdot (q^{n - r} + ... + 1)}{1 \cdot (q + 1) \cdot (q^{2} + q + 1) \cdot ... \cdot (q^{r - 1} + ... + 1)}, \end{matrix}

és ez tetszés szerint megközelíti az

\begin{matrix} \frac{n}{1} \cdot \frac{n - 1}{2} \cdot ... \cdot \frac{n - r + 1}{r} = (\binom{n}{r}) \end{matrix}

(1.1*)

közönséges binomiális együtthatót, ha

q

elég közel van az 1-hez.

2. A bimoniális tétel egy általánosítása. Vezessük be az

x

változó következő polinomját:

\begin{matrix} f (x) = (1 + x) (1 + q x) \cdot ... \cdot (1 + q^{n - 1} x); \end{matrix}

(2.1)

ennek a gyökei

n

elemű mértani sorozatot alkotnak

q^{- 1}

hányadossal és

- 1

első elemmel. Tűzzük ki következő feladatunkul az

\begin{matrix} f (x) = Q_{0} + Q_{1} x + Q_{2} x^{2} + ... + Q_{n} x^{n} \end{matrix}

(2.2)

x

hatványai szerint rendezett alak együtthatóinak meghatározását. Nyilvánvaló, hogy

\begin{matrix} Q_{0} = 1, Q_{n} = q^{n (n - 1) / 2} . \end{matrix}

(2.3)

Feladatunk megoldásában segítségünkre lesz annak észrevétele, hogy (2.1)-ből azonnal következik az

\begin{matrix} (1 + x) \cdot f (q x) = f (x) \cdot (1 + q^{n} x) \end{matrix}

(2.4)

összefüggés, vagy beírva ide (2.2)-t, azt kapjuk, hogy

\begin{matrix} (1 + x) (Q_{0} + Q_{1} q x + ... + Q_{r} q^{r} x^{r} + ... + Q_{n} q^{n} x^{n}) = & (2.5) \\ = (1 + q^{n} x) (Q_{0} + Q_{1} x + ... + Q_{r} x^{r} + ... Q_{n} x^{n}) . \end{matrix}

A két oldalon

x

hatványainak az együtthatóit összehasonlítva azt kapjuk, hogy

\begin{matrix} Q_{r} q^{r} + Q_{r - 1} q^{r - 1} = Q_{r} + q^{n} Q_{r - 1} \end{matrix}

(2.6)

vagy átrendezve

\begin{matrix} Q_{r} = Q_{r - 1} \cdot \frac{q^{n - r + 1} - 1}{q^{r} - 1} \cdot q^{r - 1}, \end{matrix}

(2.7)

r = 1, 2, 3, ..., n

(2.7)

ismételt alkalmazása

(2.3)

és

(1.1)

figyelembevételével azt adja, hogy

\begin{matrix} Q_{r} = [\binom{n}{r}] q^{r (r - 1) / 2} . \end{matrix}

(2.8)

Így

(2.1)

és

(2.2)

alapján azt kapjuk, hogy

\begin{matrix} (1 + x) (1 + q x) \cdot ... \cdot (1 + q^{n - 1} x) = & (2.9) \\ = [\binom{n}{0}] + [\binom{n}{1}] x + ... + [\binom{n}{r}] q^{r (r - 1) / 2} x^{r} + ... + [\binom{n}{n}] q^{n (n - 1) / 2} x^{n}, \end{matrix}

és ha

q

1

-hez közeledik, határesetként az

\begin{matrix} {(1 + x)}^{n} = (\binom{n}{0}) + (\binom{n}{1}) x + ... + (\binom{n}{n}) x^{n} \end{matrix}

(2.9*)

binomiális tételt, kapjuk.

3. Rekurziós formula.

(2.9)

bal oldalából az

n

helyett

n + 1

-hez tartozó megfelelő kifejezést úgy kapjuk, hogy

(1 + q^{n} x)

-szel szorzunk. A jobb oldalakból a kétféle átalakítással az

\begin{matrix} (1 + q^{n} x) ([\binom{n}{0}] + [\binom{n}{1}] x + ... + [\binom{n}{r}] q^{r (r - 1) / 2} x^{r} + ... + [\binom{n}{n}] q^{n (n - 1) / 2} x^{n}) = \\ = [\binom{n + 1}{0}] + ... + [\binom{n + 1}{r}] q^{r (r - 1) / 2} x^{r} + ... + [\binom{n + 1}{n + 1}] q^{(n + 1) n / 2} x^{n + 1} \end{matrix}

összefüggést kapjuk, és a két oldalon

x

egyenlő hatványainak az együtthatóit összehasonlítva azt nyerjük, hogy

\begin{matrix} [\binom{n + 1}{r}] = [\binom{n}{r}] + [\binom{n}{r - 1}] q^{n - r + 1}, r = 1, 2, ..., n . \end{matrix}

(3.1)

Ez az eredmény könnyen nyerhető közvetlenül az

(1.1)

definícióból is és a közönséges binomiális együtthatókra vonatkozó

\begin{matrix} (\binom{n + 1}{r}) = (\binom{n}{r}) + (\binom{n}{r - 1}) \end{matrix}

(3.1*)

összefüggésnek felel meg.
Az (1.2) "kezdeti feltételek''-ből kiindulva és sorra áttérve a (3.1) rekurziós formula alapján egy‐egy

n

értékről a rákövetkezőre, könnyen kiszámíthatjuk a Gauss‐féle binomiális együtthatókat. Eközben csak összeadást és szorzást kell ismételten végezni, kivonást és osztást soha. Ezzel azt derítettük ki

[\binom{n}{r}]

-ről, ami az

(1.1)

definíció alapján

q

racionális törtfüggvényének látszik, hogy

q

-nak egy

\begin{matrix} [\binom{n}{r}] = A_{n, r,0} + A_{n, r,1} q + ... + A_{n, r, (n - r)} q^{r (n - r)} \end{matrix}

(3.2)

alakú polinomja, és az

A_{n, r, α}

együtthatók pozitív egész számok. (A közönséges binomiális együtthatók is az

(1. 1^{*})

definíció alapján eredetileg racionális számnak látszanak, de kiderül róluk, pl.

(2. 9^{*})

-ból, hogy egész számok.) Az, hogy a

(3.2)

jobb oldalán álló polinom fokszáma

r (n - r)

, adódik pl. az

(1.1)

jobb oldalán álló kifejezés számlálójában és nevezőjében álló polinomok fokszámának különbségéből, vagy igazolható teljes indukcióval.
E dolgozat fő célja az

A_{n, r, α}

együtthatók egy szemléletes tulajdonságának a kifejtése.

4. Egy kombinatorikus értelmezés. Tekintsünk a síkban egy derékszögű koordináta-rendszert. Azokat a pontokat, amelyeknek mind a két koordinátája egész szám, rácspontoknak szokás nevezni. Gondoljuk ezeket utcasaroknak, és az utcasarkokon át a tengelyekkel párhuzamosan futó egyeneseket utcának. Képzeljünk egy ebben az úthálózatban sétáló gyalogost (mozgó anyagi pontot). Ebben az úthálózatban egy a (0, 0) és az (

(r, n - r)

sarok közt futó legrövidebb utat (feltesszük, hogy

0 ≦ r

≦ n

) zegzugos útnak fogunk nevezni; az ilyenek hossza

n

. Ismeretes,³ hogy a zegzugos utak száma

(\binom{n}{r})

. Ezt a következővel fogjuk kiegészíteni:

Tétel: Az olyan zegzugos utak száma, amelyek alatt

α

nagyságú terület van,

A_{n, r, α}

.⁴
Az "út alatti terület''-et az út, a vízszintes

y = 0

tengely és a függőleges tengellyel párhuzamos

x = r

egyenes zárja körül.

Az 1. ábra az

n = 6

r = 2

speciális esetet szemlélteti.
A binomiális együtthatókra vonatkozó állítás szinte csak átfogalmazása a

(3. 1^{*})

rekurziós egyenlőségnek. A (2, 4) sarokra vagy a (2, 3) vagy az (1, 4) sarokról érkezhetünk zegzugos úton, így az előbbi sarokra vezető utak száma az utóbbi kettőre vezető utak számának az összege. Miután még a függőleges és a vízszintes tengelyen levő

(0, n)

és

(n,0)

sarkok mindegyikére csak egy‐egy zegzugos út vezet, összhangban az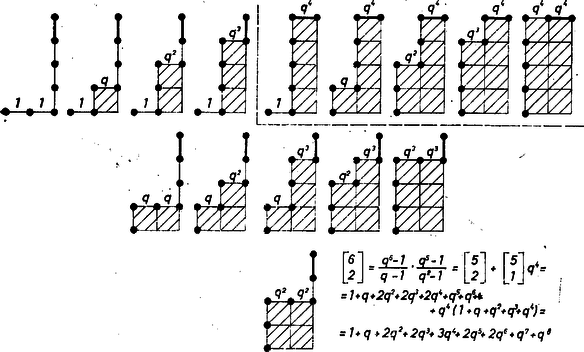

\begin{matrix} (\binom{n}{0}) = (\binom{n}{n}) = 1 \end{matrix}

"peremfeltételekkel'', így az egy‐egy sarokra vezető zegzugos utak száma ugyanazokat a feltételeket elégíti ki, mint a megfelelő binomiális együttható. A kettő tehát megegyezik.

1. ábra

Egész hasonlóan értelmezhetjük a

(3.1)

rekurziós formulát is. Most minden zegzugos úthoz

q

egy hatványát fogjuk hozzárendelni, és az egy sarokra vezető utakhoz rendelt tagok összege lesz a megfelelő Gauss‐binomiális együttható. A (2, 4) sarokra vezető 6 hosszúságú zegzugos utakat tekintsük két részből: a (0, 0) sarokról induló 5 egységnyi hosszúságú kezdő részből és a (2, 4) sarokra érkező 1 hosszúságú záró szakaszból állónak.
A

(3.1)

-ből esetünkben adódó

\begin{matrix} [\binom{6}{2}] = [\binom{5}{2}] + [\binom{5}{1}] \cdot q^{4} \end{matrix}

összefüggés jobb oldalának első tagja képviseli a (2, 3) sarokról érkező

(\binom{5}{2}) = 10

zegzugos út adalékát, tehát azokét, amelyeknek a záró szakasza függőleges, a második tag pedig az (1, 4) sarokról érkező, tehát vízszintes zárószakasszal rendelkező

(\binom{5}{1}) = 5

zegzugos út adalékát. Az előbbi zegzugos utakhoz

q

-nak ugyanazt a hatványát fogjuk rendelni, mint a kezdő részükhöz, az utóbbiakhoz pedig a kezdő részükhöz rendelt hatvány

q^{4}

-szeresét, vagyis 4-gyel magasabb hatványt.

Ezt úgy is fogalmazhatjuk, hogy a függőleges útszakaszokhoz 1-et rendelünk hozzá, a 4 magasságban futó egységnyi hosszúságú vízszintes szakaszhoz pedig

q^{4}

-t. Általában minden

h

magasságban futó egységnyi hosszúságú vízszintes útszakaszhoz

q^{h}

-t rendelünk, speciálisan a vízszintes tengelyen levő szakaszokhoz

q^{0} = 1

-et. Egy zegzugos úthoz ezután az egységnyi szakaszaihoz rendelt értékek szorzatát rendeljük. Így a függőleges és a vízszintes tengelyeken levő

(0, n)

és

(n,0)

sarkokra vezető egyetlen zegzugos út minden szakaszához 1-et rendeltünk, tehát az egész úthoz is. Ez összhangban van az

(1.2)

peremfeltétellel. A

q

hatványainak a vízszintes és függőleges szakaszokhoz történt hozzárendelése is általában összhangban van

(3.1)

-gyel, mert a jobb oldal első tagja az

(r, n - r)

sarokról, a második pedig az

(r - 1, n - r + 1)

sarokról az

(r, n - r + 1)

sarokra érkező utak adalékát tartalmazza. Az 1. ábrán feltüntettük a vízszintes szakaszokhoz rendelt értékeket. Az elmondottakat jól követhetjük az ábra alapján.

Ezzel tehát beláttuk, hogy az

[\binom{n}{r}]

Gauss‐binomiális együttható a (0, 0) sarokról az

(r, n - r)

sarokra vezető zegzugos utakhoz tartozó

q

-hatványok összege; ennek a hatványnak a kitevője az út vízszintes szakaszaihoz rendelt hatványok kitevőinek összege.
Az egyes szakaszokhoz rendelt kitevő viszont azt mutatja, hogy a szakasz hány egység magasságban van, vagy még másképp fogalmazva: hány egységnyi oldalú négyzet helyezhető el a szakasz és a vízszintes tengely közt. Az egész úthoz rendelt kitevő tehát az út vízszintes szakaszai alatt levő területek összegével, vagyis az egész zegzugos út alatti területtel egyezik meg. Így valóban

q^{α}

együtthatója az olyan zegzugos utak száma, amelyek alatt

α

terület van, és éppen ezt állítja tételünk.
Tanulságos lesz közvetlenül igazolni néhány olyan összefüggést, ami szoros kapcsolatban van az éppen látott tétellel.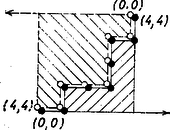

2. ábra

Akár a 2. ábrából, akár az

(1.1)

kifejezésből világos (ábra a 102. oldalon), hogy

\begin{matrix} A_{n, r, α} = A_{n, r, r (n - r) - α} . \end{matrix}

(4.1)

Mivel továbbá

q = 1

-nél

(1.3)

szerint a Gauss‐féle binomiális együttható a megfelelő közönséges binomiális együtthatót adja, így

(3.2)

azt szolgáltatja, hogy

\begin{matrix} A_{n, r,0} + A_{n, r,1} + ... + A_{n, r, (n - r)} = (\binom{n}{r}) . \end{matrix}

(4.2)

5. Egy további kombinatorikus értelmezés. Egy zegzugos út egymáshoz csatlakozó egységnyi szakaszokból áll, amelyek szomszédos utcasarkokat kötnek össze. Ezeket a szakaszokat a (0, 0) pontból indulva sorra

x

-szel vagy

y

-nal fogjuk megjelölni aszerint, hogy melyik melyik koordináta‐tengellyel párhuzamos. Ezzel egyértelműen egymáshoz rendeltük a zegzugos utakat és betűsorozatok egy halmazát; a 2. ábrán mutatott példában a zegzugos út az (5, 4) saroknál végződik, és a megfelelő sorozat 9 betűből áll.

3. ábra

Osszuk az

(r, n - r)

végpontú zegzugos út alatti területet az

y

-tengellyel párhuzamos, egyenlő távolságra következő egyenesekkel

r

téglalapra, melyek alapja 1 egység, magasságaik (balról jobbra sorolva fel őket)

\begin{matrix} 0, 1, 3, 3, 4. \end{matrix}

Mindegyik téglalap felső oldala a zegzugos út egy egységnyi vízszintes szakasza, és így a betűsorozatban egy

x

-nek felel meg. A téglalap magasságát (egyben az előzőkben a felső vízszintes szakaszához rendelt

q

-hatvány kitevőjét), és így a területét is, a szóban forgó

x

-et megelőző

y

-ok száma adja meg. Ezt úgy is mondhatjuk, hogy a téglalap területe megegyezik a szóban forgó

x

alkotta inverziók számával ebben a betűsorozatban. Akkor mondjuk, hogy a sorozat betűiből kiválasztható

n (n - 1) / 2

pár közül vett valamelyik pár inverziót alkot, ha a pár egy

x

-ből és egy azt megelőző

y

-ból áll. Az

r

téglalap együttes területe tehát, vagyis a zegzugos út alatti terület megegyezik a betűsorozatban előforduló inverziók számával (példánkban ez 11).
A Gauss‐féle binomiális együtthatók tehát nemcsak a zegzugos utak alatt területeket sorolják fel, hanem ezzel együtt az éppen vizsgált betűsorozatokban fellépő inverziók számát is. A Gauss‐féle binomiális együtthatóknak ez a kapcsolata ismeretes volt.⁵ Mi itt a területekről az inverziókra történő szemléletes áttérés lehetőségét kívántuk hangsúlyozni.⁶
A probléma megközelíthető egy egészen eltérő úton is. Erre a dolgozat második részében térünk vissza.
Pólya György
Stanford University,
Stanford, Calif., USA

¹Megjelent az Elemente der Mathematik 26 (1971), 102‐109. oldalán. Fordította a K.M.L. céljára kisebb módosításokkal Surányi János.

²Vö. Carl Friedrich Gauss, Summatio quarundam serierum singularium. Összegyűjtött művei 2. köt., főképp 16‐17. o.

³Lásd pl. Pólya György: A problémamegoldás iskolája I. Tankönyvkiadó, Budapest, 1967. 81‐86. old.

⁴G. Pólya, Journ. of Combinatorial Theory 6 (1969) 102‐105. old., különösen 105. old.

⁵Lásd pl. M.G. Kendall‐A. Stuart: The advanced Theory of statistics II. (London 1961) 494. old.

⁶G. Pólya: Proceedings of the second Chapel Hill Conference on Combinatorial Math. and its Applications (1970) 381‐384. A 4. és 5. bekezdés nagy részét a szervező bizottság szives engedelmével e cikkből vettük át.