|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. Az 1971. évi Kürschák József matematikai tanulóverseny 2. feladatának megoldásai azt adták eredményül, hogy ha adva van a síkban pont, amelyek közt nincs 3 egy egyenesen levő, akkor ezekből kiválaszthatók párok (minden pont legfeljebb egy párban szerepelhet) úgy, hogy az egy párba tartozó pontokat összekötve a szakaszoknak legalább különböző metszéspontja legyen. (A versenyfeladat az esetre vonatkozott.)
A III. megoldáshoz fűzött 2. megjegyzés felveti az állítás élességének kérdését: Vajon ennyi pont birtokában nem lehet-e lényegesen több metszéspontot is létrehozni, illetőleg metszéspont létrehozásához nem elegendő-e kevesebb pont megadása is ? Akármilyen egyszerű is a kérdés, a válaszról vajmi keveset tudunk egyelőre.
Világos, hogy -re nem élesíthető a tétel, hiszen egy háromszög és a belsejében egy pont még nem szolgáltat metszéspontot, és pl. egy konvex négyszög a belsejében egy ponttal csak egy metszéspontot ad.
2. Mégis az várható, hogy a pontok számának növekedésével a köztük alkalmasan húzott, közös végpont nélküli szakaszok különböző metszéspontjainak a száma erősebben növekszik, mint egyenes arányosság szerint.
Fel is merül egy gondolat a feladatra adott megoldások javítására. Mindegyik megoldásban felhasználást nyert az a tétel, hogy a sík általános 5 pontja közt mindig szerepelnek egy konvex négyszög csúcsai. Ezt Klein Eszter vette észre mint egy általa felvetett általános probléma speciális esetét. Azt kérdezte ő, létezik-e minden -hoz olyan szám, és ha igen, mi a legkisebb szám, amire igaz, hogy a sík általános pontja közül mindig kiválaszthatók egy konvex -szög csúcsai. Az említett eredmény szerint és világos, hogy . Makai Endre és Turán Pál megmutatta, hogy . Általában csak annyi ismeretes, hogy létezik, mégpedig azaz pont még megadható úgy, hogy ne szerepeljenek köztük egy konvex -szög csúcsai, de pont közül már mindig ki lehet választani ilyen pontot. A sejtés az, hogy . Az első 3 érték ennek megfelel.
3. Ez a felvetett problémához úgy csatlakozik, hogy egy konvex oldalú sokszögben létre lehet hozni metszéspontot közös végpont nélküli átlókkal, amint azt esetére az 1. ábra mutatja. 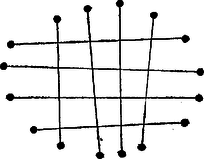 1. ábra
Ha most már elég nagy, és úgy bontunk pontot a versenyfeladat I. megoldása gondolatmenetének megfelelően részekre párhuzamos egyenesekkel, hogy az első csoport pontból álljon, mindegyik további pontból, akkor így konvex -szögeket tudunk kiválasztani, a fölöslegesen maradó pontokat mindig továbbvíve a következő ponthoz. Ilyen módon, ha elég nagy, sok metszéspontot tudunk létrehozni. Nem nehéz kiszámolni, hogy ha -t -től függően elég nagyra választjuk, akkor ilyen módon egy alkalmas pozitív számértékkel létre lehet hozni számú metszéspontot.
A baj csak az, hogy növekedésével nem egy‐két, hanem nagyon sok pontot kell csatolnunk az egyik tartomány pontjai közül a következő tartományéihoz, és így a párhuzamos elválasztó egyenesek mit sem védenek a metszéspontok összeesése ellen.
4. Ha viszont nem vagyunk tekintettel a metszéspontok különbözőségére, akkor megmutatható, hogy van olyan szám, hogy pont közt alkalmasan húzott, közös végpont nélküli szakaszokkal metszőpár keletkezik. Könnyen elképzelhető, hogy a metszéspont‐egybeesések nem lehetnek nagyon gyakoriak, annyira, hogy egy -nél kisebb állandóval páronként különböző metszéspont is mindig létrehozható.
5. A következőkben azt fogjuk megvizsgálni ‐ most már sejtések és feltételezések nélkül ‐, hogy hány pont megadása szükséges metszéspont biztosításához. Az eredményt kissé meglepőnek találtam és figyelmeztetőnek abban az irányban, hogy túl vérmes reményeket sem szabad táplálni.
a) Ha 6 pont egy konvex hatszög csúcsait alkotja, akkor már biztosítanak 2 metszéspontot, amint azt a . ábra mutatja. Az ábra arra is utal, hogy több metszéspont már ebben az esetben sem mindig biztosítható a lehetséges egybeesések miatt.
b) Itt nem a hatszög konvexsége a lényeges. Ha egy konvex ötszög egyik átlója levágta háromszög tartalmaz még egy pontot, pl. a háromszög egy pontot, akkor is már biztosítható 2 metszéspont. Az és háromszögek egyike ugyanis nem tartalmazza -et, mondjuk az előbbi ilyen. Ekkor és különböző pontokban metszi a átlót (. ábra).
c) Már az is elég 2 metszéspont létrehozására, hogy egy konvex négyszögben pl. a átló mindkét oldalán legyen még egy‐egy pont, mondjuk az -val egy oldalon , -vel egy oldalon (2c. ábra). Ekkora két átló és ad két metszéspontot, kivéve, ha egy ponton mennek keresztül (az ábrán és ). Ez esetben viszont és metszi -t két különböző pontban.
d) Ha egy konvex ötszög átlói körülzárta ötszögben választunk ki egy pontot, akkor már nem tudunk létrehozni 2 metszéspontot. A 6 pont között ugyanis legfeljebb 3 szakaszt tudunk meghúzni, tehát ezek valamelyikén rajta kell lennie mind a két metszéspontnak. Viszont az -ből induló szakaszokon csak egy‐egy metszéspont van; az ötszög átlóin ugyan 3 (3. ábra), de az ezeket kimetsző szakaszok egyik végpontja közös, így közülük csak egy jelölhető ki. 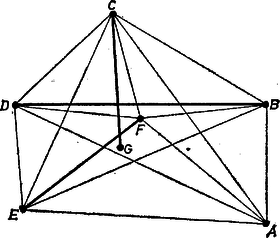 3. ábra
e) Ha az előbbi átlók körülzárta ötszögben még egy hetedik pontot is választunk, már ismét biztosítható 2 metszéspont. Ha ugyanis pl. az háromszögben van, akkor metszi -t és , közül az egyiket. Ezek a metszéspontok különbözők, mert sem -nek, sem -nek nincs közös pontja -vel.
6. a) Eddig annyira jutottunk, hogy 6 pont még nem feltétlenül elég 2 metszéspont biztosításához. Ha viszont több pontot is ki lehet jelölni úgy, hogy köztük futó közös végpont nélküli szakaszoknak legfeljebb 1 metszéspontja legyen, akkor az ilyen ponthalmaz konvex burka csak háromszög vagy négyszög lehet.
b) A 4. ábra néhány olyan 7 pontból álló pontrendszert mutat, amelyben 1-nél több metszéspont nem hozható létre közös végpont nélküli szakaszokkal. Folytonos vonallal húztuk meg azokat a szakaszokat, amelyeket valamely szakasz metsz, és könnyen ellenőrizhető, hogy az egy‐egy szakaszt metsző szakaszok egyik végpontja minden esetben közös és mivel csak 3 szakaszt tudunk kijelölni, láttuk 5. d)-ben, hogy így nem hozható létre 2 metszéspont. 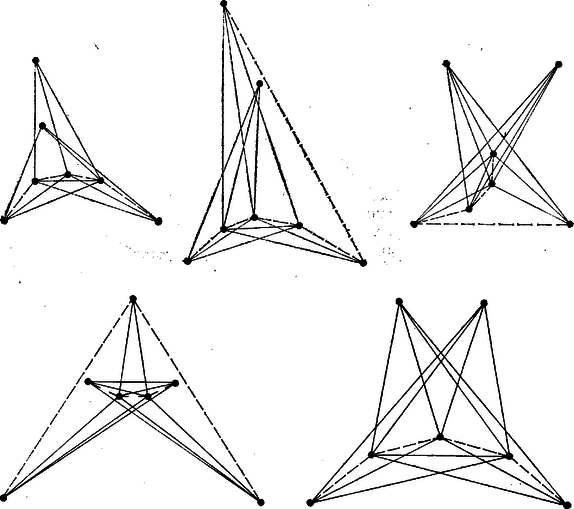 4. ábra
7. Vizsgáljuk meg a 8 pontból álló pontrendszereket. Tudjuk, hogy eleve elég az olyan pontrendszereket vizsgálni, amelyeknek a konvex burka háromszög vagy négyszög, és ha négyszög, akkor a további pontoknak 5. c) értelmében az átlók közti négy háromszög egyikében kell mindnek lenniük.
a) Legyen az négyszög a konvex burok és a további pontok feküdjenek az oldalhoz csatlakozó háromszögben. Ha egy itteni pontot -vel vagy -vel összekötő szakasz átmetszi másik két pont összekötő szakaszát, akkor már rendelkezésre áll 2 metszéspont, mert átmetszi az egyik négyszögátlót is (5. ábra, pont). 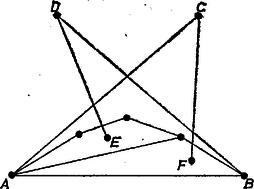 5. ábra
A és elhagyásával maradó pontok konvex burka 5. a) szerint nem lehet hatszög, de ötszög sem, mert ez tartalmazna még egy pontot, az azt -vel összekötő szakasz azonban az előző megállapítás szerint az ötszögnek csak egyik, az -vel szomszédos oldalát metszheti. Ekkor azonban benne van két szomszédos ötszögoldal meghatározta háromszögben (5. ábra, pont) és ekkor 5. b) szerint létrehozható 2 metszéspont.
Ha a 6 pont konvex burka négyszög, az 2 pontot tartalmaz még, jelöljük és -fel. Az ezeket -vel és -vel összekötő szakaszok ismét csak a konvex burok -vel szomszédos oldalait metszhetik (6. ábra). 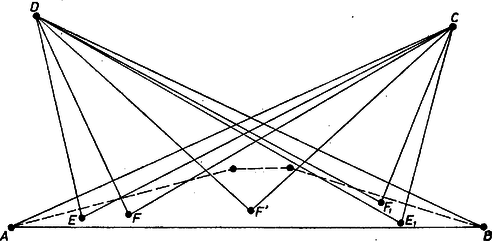 6. ábra
Ha konvex négyszög, akkor és különböző pontokban metszi vagy ugyanazt a szakaszt ( és pont) vagy két közös végpont nélküli szakaszt ( és pont). Ha pedig pl. a háromszögben van ( és pont), akkor pl. ismét és két különböző pontban metsz egy szakaszt.
Ha végül a 6 pont konvex burka egy háromszög (7. ábra), akkor egyrészt az elhagyásával maradó 7 pont közül 3 a négyszögön kívül van, másrészt 6. a) szerint a konvex burkuk legfeljebb négyoldalú. Így egy négyszög lesz. Hasonlóan a elhagyásával maradó pontok konvex burka egy négyszög, ahol és egybe is eshet. 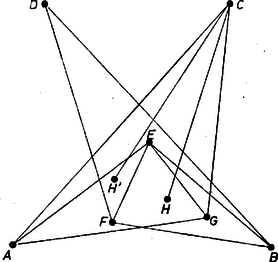 7. ábra
A nyolcadik pont, nem lehet az , , és határolta négyszögben (ha ez egyáltalán létrejön), mert akkor a szakasz metszené az , szakaszok valamelyikét (7. ábra, ), ami 7. a) szerint nem lehet. De nem fekhet pl. az , , közötti háromszögben sem (7. ábra, pont), mert ekkor -t és -t metszené .
8. Az a lehetőség maradt csak tehát hátra, hogy a 8 pont konvex burka egy háromszög legyen. Ekkor a valamelyik csúcs elhagyásával maradó 7 pont konvex burka ismét csak háromszög vagy négyszög lehet. Ha pl. a csúcs elhagyásával maradó pontok konvex burka az négyszög és a másik 4 pont is konvex négyszöget határoz meg (8. ábra), akkor az utóbbinak -ből induló átlóját metszi a másik átló és az konvex burok egy oldala is. 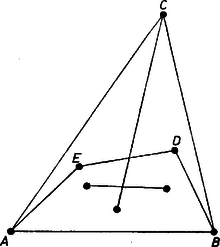 8. ábra
Feltehetjük tehát, hogy a további , , pontok közül az utolsót tartalmazza a háromszög.
Ha , , az háromszögben van (. ábra), akkor metszi -t és a háromszög egy oldalát. Hasonló a helyzet, ha a 3 pont a háromszögben van.
Ha az , , szakaszok közt keletkező háromszögben vannak a pontok, akkor , , legalább 3 különböző pontban metszi az , átlókat, tehát valamelyiken, mondjuk az utóbbin, legalább 2 metszéspont, a -é és a -é keletkezik. Ekkor és vagy és különböző pontokban metszi -t (. és . ábra).
Az a lehetőség maradt még, hogy akár -t, akár -t, akár -t hagyjuk el, a maradó pontok konvex burka a , , ill. háromszög. A további 2 pont ez esetben a 3 háromszög közös részeként létrejövő hatszögben van.
Ha van egy pont pl. az , , szakaszok közt keletkező háromszögben, akkor metszi -t és , egyikét (. ábra). 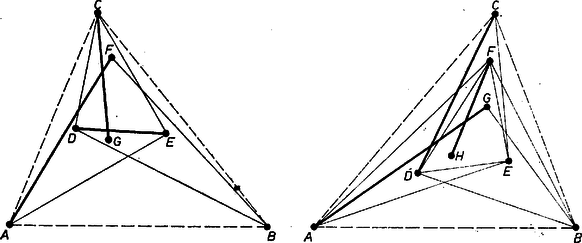 10a. ábra 10b. ábra
Ha viszont a háromszögben van még két pont, és , és pl. az háromszögben fekszik, akkor metszi az , szakaszok egyikét, mert mint az konvex burok csúcsa az háromszögön kívül van (. ábra). Mondjuk -t metszi. Ezt metszi azonban és egyike is, mert az elhagyásával maradó 7 pont konvex burka.
Ezzel az összes lehetséges eseteket végigpróbáltuk, és azt találtuk, hogy a sík bármely 8 általános helyzetű pontja közt meghúzhatók közös végpont nélküli szakaszok úgy, hogy azoknak legyen 2 különböző metszéspontjuk. Mint a versenyfeladathoz fűzött megjegyzésekből tudjuk, ebből már következik, hogy ha , akkor pont között mindig meghúzhatók közös végpont nélküli szakaszok úgy, hogy azoknak legalább különböző metszéspontja legyen.
A versenyfeladatban szereplő 5 metszéspont tehát már 20 pont megadásával is biztosítható.
Surányi János: Az 1971. évi Kürschák József matematikai tanulóverseny feladatainak megoldása. K. M. L. 44 (1972) 51‐58.Ugyanott, 56. oldal.Jelenleg Szekeres Györgyné (Sidney, Ausztrália).Lásd Erdős P.‐Szekeres Gy. cikkeit: Compositio Math. 2 (1935) és Annales Univ. Sci. Budapestiensis, Sectio Math. 3‐4 (1960‐61); továbbá P. 85 probléma, K.M.L. 44 (1972) 72.Lásd az idézett cikkben, az 55. oldalon. |
 PDF | MathML
PDF | MathML