Cím: 1971. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Surányi János 
Füzet: 1972/február, 51 - 58. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Egy egyenes az ABC háromszög AB oldalát C1-ben, AC oldalát B1-ben, a BC oldal meghosszabbítását A1-ben metszi. Legyen C1-nek, illetve B1-nek a rajta átmenő oldal felezőpontjára vonatkozó tükörképe C2, illetve B2, továbbá a B2C2 és BC egyenesek metszéspontja A2. Bizonyítandó, hogy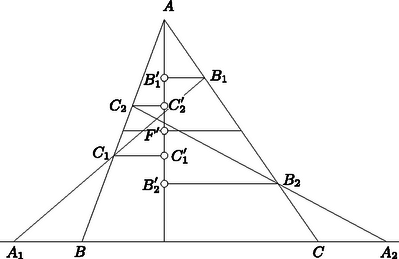

sinB1A1C∢:sinC2A2B∢=B2C2:B1C1.

 
I. megoldás. Jelöljük a B1, B2, C1, C2 pontok merőleges vetületét a háromszög A-ból húzott magasságán B'1, B'2, C'1, C'2-vel. Az AB és AC oldal felezőpontjainak a vetülete a magasságon ugyanaz az F' pont, miután a felezőpontokat összekötő egyenes, a háromszög középvonala, párhuzamos a BC oldallal, tehát merőleges az A-ból húzott magasságra (1. ábra). Így a B'1C'1 és a B'2C'2 szakaszok is egymás tükörképei, tehát egyenlő hosszúak (és ellenkező irányúak).
 
 

1. ábra
 

A B'1B1C1∢ és a B1A1C∢, továbbá a C'2C2B2∢ és a C2A2B∢ szárai párhuzamosak, tehát sinusaik megegyeznek. Így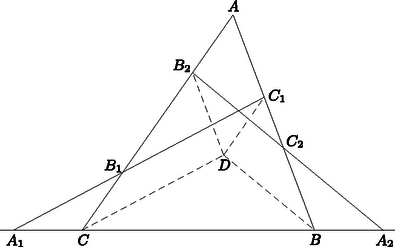
sinB1A1C∢=sinB'1B1C1∢=B'1C'1B1C1,sinC2A2B∢=sinC'2C2B2∢=C'2B'2B2C2.
A jobb oldali törtek számlálói egyenlők, így a bal és a jobb oldalak hányadosa is megegyezik, ami a kívánt egyenlőséget adja.
 
II. megoldás. Toljuk el a B1C1 szakaszt a B1C vektorral, legyen C1 új helyzete D (2. ábra). Ekkor
C1D=B1C,
és a két szakasz egyirányban párhuzamos. A tükrözés folytán viszont az utóbbi szakasz AB2-vel egyenlő és egyirányú. Így AB2DC1 paralelogramma, tehát B2D, AC1 és ‐ ismét a tükrözés folytán ‐ C2B egyirányú, egyenlő szakaszok. Ez viszont azt jelenti, hogy BC2B2D is paralelogramma, DB tehát B2C2-ből keletkezik párhuzamos eltolással.
 
 

2. ábra
 

A keletkezett BCD háromszögben DCB∢ és DBC∢ szárai párhuzamosak a B1A1C∢, ill. C2A2B∢ száraival, s így sinusaik megegyeznek.
A BCD háromszögre a sinustételt alkalmazva nyerjük, hogy
BDCD=B2C2B1C1=sinDCB∢sinDBC∢=sinB1A1C∢sinC2A2B∢.
Ezt kellett bizonyítanunk.
 
Megjegyzések. 1. Egyik bizonyításban sem használtuk ki azt, hogy B1 és C1 a megfelelő oldalszakaszon van. Így a feladat állítása igaz minden olyan egyenesre, amelyik metszi mind a három oldalegyenest és nem megy át A-n.
2. A feladat szövege kimondta ugyan, hogy a B2C2 és BC egyenes metszi egymást, több versenyző rámutatott azonban, hogy ez következik már abból, hogy B1C1 és BC metszik egymást. Valóban, az I. megoldásban az utóbbi tény azt jelenti, hogy B'1 és C'1 különböző, de ekkor B'2 és C'2 is, tehát B2C2 sem párhuzamos BC-vel. A II. megoldásban a feltétel azt jelenti, hogy D nem esik BC-re. Ekkor azonban DB és a vele párhuzamos B2C2 sem párhuzamos BC-vel.
3. Többen vektorszámítással oldották meg a feladatot, megmutatva hogy a B1C→1+B2C→2 eredővektor párhuzamos (sőt egyenlő) a CB→ vektorral. Ez könnyen adódik, ha pl. a fellépő vektorokat a CA→ és AB→ vektorokkal párhuzamos összetevőkre bontjuk.
 
Második feladat. Adott a síkban 22 pont, közülük semelyik három sincs egy egyenesen. Bizonyítsuk be, hogy párokba oszthatók úgy, hogy az egy párba tartozókat összekötő szakaszoknak legalább 5 különböző metszéspontja legyen.
 
A feladat követelményei szerint három dolgot kell szem előtt tartanunk: minden pontot csak egy másikkal köthetünk össze, a metszéspontoknak a szakaszokra kell esniük és nem szabad egybeesniük.
Két metsző szakasz végpontjainak a kiválasztása ugyanaz a feladat, mint egy konvex négyszög csúcsaié, mert konvex négyszög átlói egymást metsző szakaszok és két egymást metsző szakasz végpontjai konvex négyszög csúcsai, amelyiknek a szakaszok az átlói.
Megemlítjük még a ponthalmaz konvex burkának a fogalmát, aminek segítségével könnyebben tudjuk magunkat kifejezni. Ezen azt a legszűkebb konvex tartományt értjük, amelyik az összes pontot tartalmazza. Ezt szemléletesen úgy képzelhetjük el, hogy a pontokban a síkra merőleges tűket gondolunk, majd egy gumikarikát kihúzunk akkorára, hogy az összes tű belül legyen rajta és elengedjük. Az összeugró gumi által körülzárt tartomány a konvex burok. Ez véges ponthalmaz esetén konvex sokszög, aminek a csúcsai a ponthalmaz pontjai közül valók.
 
I. megoldás. Fel fogjuk használni, hogy 5 pont közül a síkban mindig kiválaszthatók egy konvex négyszög csúcsai, ha nincs köztük 3 egy egyenesen levő pont.
Valóban, ha az 5 pont konvex burka ötszög, akkor bármelyik 4 pont megfelel. Ha négyszög a konvex burok (amelyik a belsejében tartalmaz még egy pontot), akkor is rendelkezésünkre áll már egy konvex négyszög. Ha a konvex burok háromszög, a belsejében 2 ponttal, akkor húzzuk meg az utóbbiakon átmenő egyenest (3. ábra). Ez 2 oldalt a belsejében metsz, mert csúcson nem mehet át, ugyanis nincs 3 pont egy egyenesen. Ekkor a harmadik oldal végpontjai és a két belső szögpont alkot konvex négyszöget.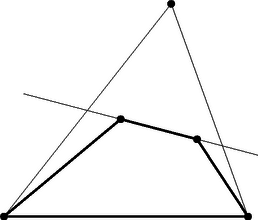
 
 

3. ábra
 

Válasszunk egy e egyenest, amelyik nem párhuzamos semelyik két ponton átmenő egyenessel. Ez lehetséges, mert véges sok pont csak véges sok irányt határoz meg. Helyezzünk el egy e-vel párhuzamos egyenest úgy, hogy a ponthalmaz az egyik partjára essék, majd mozgassuk, irányát megtartva, a pontrendszer irányában és jelöljük meg 4 helyzetét, az elsőt úgy, hogy 5 pont kerülön át az egyenes ellenkező partjára, majd következő hármat úgy, hogy 4‐4 újabb pont kerüljön át a másik oldalra. Ekkor még 5 pont marad az első parton.
Az első 5 pont közül ki tudjuk választani két metsző szakasz végpontjait és marad még egy pont, ezt vegyük a következő négyhez és ismét válasszuk ki két metsző szakasz végpontjait. A fennmaradó ponttal ismételjük az eljárást és folytatjuk, amíg mindegyik pontcsoportot fel nem használjuk.
Így 5 szakaszpárt választottunk ki. Ezek kiválasztásuk szerint egymást metsző szakaszokból állnak és nincs kettőnek közös végpontja. A metszéspontok is mind különbözők, mert mindegyik szakaszpár négy végpontja közül legalább hármat, s így az egyik szakasz mindkét végpontját, egy
e-vel párhuzamos egyenes elválaszt a korábban kiválasztott szakaszoktól, tehát a szakasz belsejében levő metszéspontot is elválasztja a korábban nyert metszéspontoktól.
Ezzel a feladat állítását igazoltuk.
 
Megjegyzések. 1. Az eljárás csak 21 pontot használt fel az 5 metszéspont létrehozásához, a huszonkettedik csak ahhoz kellett, hogy a párokba állítás lehetséges legyen. Ugyanez az eljárás általában 4n+1 szögpontból n különböző metszéspont létrehozását teszi lehetővé.
2. Többen úgy választották meg a 3 síksávot és 2 félsíkot, hogy a ponthalmazból 5‐5‐5‐5, ill. 2 pontot tartalmazzanak. Ekkor utolsó lépésben az első 4 metszéspont kiválasztásakor fennmaradt pontok és az utolsó két pont közül lehet még egy metsző szakaszpár P, Q és R, S végpontjait kiválasztani. Tegyük fel, hogy ezek metszéspontja egybeesik egy másik szakaszpár pl. AB és CD metszéspontjával (4. ábra). Ekkor az előbbi pár legalább egyik szakaszának mind a két végpontja másik síkrészben van, mint a metszéspont.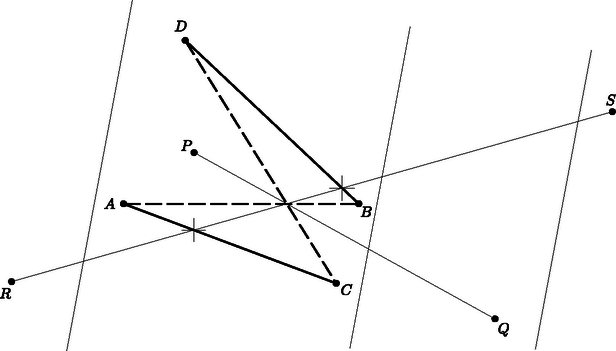
 
 

4. ábra
 

Ha RS ilyen szakasz, akkor ez metszi az ACBD négyszög két szemben fekvő oldalát, mondjuk AC-t és BD-t, tehát ezek a szakaszok és RS két különböző metszéspontot szolgáltatnak. Ezek különböznek a további metszéspontokból is, mert ugyanabban a síkrészben vannak, mint az eredeti metszéspont (ami különben továbbra is létrejön mint az eddig még figyelmen kívül hagyott PQ metszéspontja RS-sel).
3. Ahelyett, hogy párhuzamos egyenesekkel osztanók csoportokba a pontokat, kiválaszthatjuk a ponthalmaz konvex burkának egy A csúcsát és ezen át egy egyenest, amelyiknek egyik partjára esik a ponthalmaz minden A-tól különböző pontja; ezután ennek egyik félegyenesét forgatva hozunk létre olyan szögtartományokat, amelyek 4‐4‐4‐4 pontot tartalmaznak A-n kívül, és A-val és az első 4 ponttal kezdve végezzük a fenti kiválasztási eljárást. A forgó félegyenes egyenként halad át a pontokon, mert három pont nem esik egy egyenesre.
 
II. megoldás. Újabb eljárást adunk meg legalább 5 pont esetén olyan metsző szakaszpár kiválasztására, amelyek metszéspontja nem eshet rá egyetlen további (esetleg) kiválasztható szakaszra sem.
Legyen a ponthalmaz konvex burkának három szomszédos csúcsa A, B és C. Ekkor az ABC konvex szögtartomány (hozzáértve a határoló félegyeneseket is) tartalmazza a ponthalmazt.
Tekintsük a B elhagyásával maradó ponthalmaz K konvex burkát. Ez is konvex sokszög, mert legalább 4 nem egy egyenesen levő pontot burkol. K határának egyik, A-tól C-ig haladó törött vonala elválasztja a halmaz legalább egy pontját B-től, kivéve ha ez a határ az AC szakaszból és egy az ABC háromszögben futó, A-t és C-t összekötő törött vonalból áll, amelyiknek az összes további pont szögpontja (5. ábra).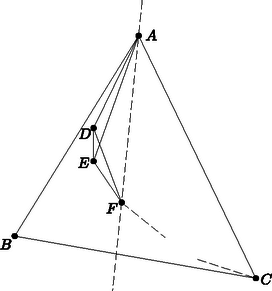
 
 

5. ábra
 

Utóbbi esetben vegyük fel pl. K-nak A-val szomszédos, D, E, F csúcsait (F azonos lehet C-vel) és válasszuk ki az AE és DF szakaszt. Ezek metszéspontja az AF egyenesnek azon a partján jön létre, amelyiken B van. A ponthalmaz többi pontja (ha van további pont) az egyenes másik partján van, így minden esetleges további szakaszpár négy végpontja közül legalább 3 az utóbbi parton van, tehát az egyik szakasz is és ha a szakaszok metszik egymást, akkor a metszéspontjuk is.
Abban az esetben, ha van a ponthalmaznak olyan D pontja, amire BD metszi K határát, akkor legyen EF az az oldal, amit átmetsz (6. ábra). Nem mehet át BD valamely csúcson, mert nincs 3 egy egyenesre eső pont a halmazban. Ekkor a halmaz minden további pontja az EF egyenes egyik partján van, a határán sem lehet, így egyetlen további szakaszpár metszéspontja sem eshet egybe BD és EF metszéspontjával.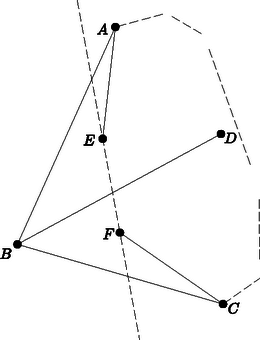
 
 

6. ábra
 

22 (sőt már 21) pontból kiindulva, az eljárást 5-ször ismételhetjük, s így 5 különböző metszéspontot tudunk létrehozni; általában 4n+1 pontból n metszéspontot.
 
Megjegyzés. 5 pont esetén újabb bizonyítást nyertünk arra az I. megoldásban felhasznált segédtételre, hogy 5 pont közül mindig kiválaszthatók egy konvex négyszög csúcsai.
 
III. megoldás. A ponthalmaz meghatározta összes szakaszok metszéspontjai közül fogunk olyat kiválasztani, amelyiken legfeljebb 3 szakasz megy át. Megmutatjuk, hogy a szakaszok összes metszéspontjai konvex burkának a csúcsai ilyenek.
Világos, hogy ezzel a feladat állítása bizonyítást nyer, ugyanis ha legalább 5 pont van adva, akkor az előző megoldásokban bizonyított segédtétel szerint legalább egy metszéspont is van. Kiválasztjuk a metszéspontok konvex burkának egy csúcsát és 2 olyan szakasz végpontjait, amelyeknek ez a metszéspontja. A maradó pontokkal addig ismételhetjük az eljárást, amíg legalább 5 pont marad, tehát 21 ponttal még 4-szer, általában 4n+1 ponttal n-szer.
A keletkező metszéspontok mind különbözők, mert 2‐2 metsző szakasz közül legfeljebb az egyik mehet át korábban kiválasztott szakaszpárok metszéspontján.
A kimondott állítást indirekt úton bizonyítjuk. Ha a metszéspontok konvex burkának egy P csúcsán át legalább 4 szakasz menne át, akkor vegyük ezeknek egy-egy, a konvex burkon kívül eső végpontját. Ezek és P közül kiválaszthatók két egymást metsző szakasz végpontjai. Ezek metszéspontja a metszéspontok halmazán kívül van és metszéspontja a ponthalmaz 4 pontja által meghatározott szakaszoknak. Valóban, vagy P nem is szerepel a kiválasztott 4 pont közt, vagy ha igen, akkora benne végződő szakasz része egy, a ponthalmaz pontjai által meghatározott szakasznak (7. ábra).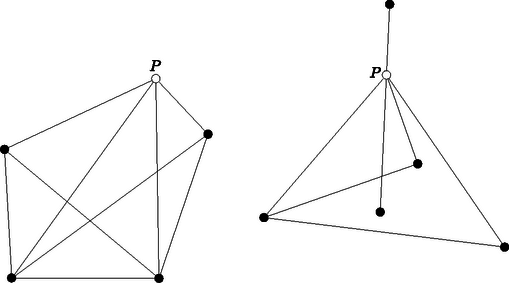
 
 

7. ábra
 

Ezzel ellentmondásra jutottunk a konvex burok fogalmával, így P-n nem mehet át 4 szakasz.
 
Megjegyzések. 1. Nem nehéz látni, hogy 3 szakasz sem mehet át a metszéspontok konvex burka határán levő metszéspontokon. Ennek bizonyítását az olvasóra bízzuk.
2. Felvetődik a kérdés, hogy 5 metszéspont létrehozására nem elegendő-e 21-nél kevesebb pont is, ill. hogy nem lehet-e bármilyen 21 pontból kiindulva 5-nél több metszéspontot is létrehozni.
Valóban, a megoldások egymástól lehetőleg elválasztott szakaszpárok kiválasztása útján biztosítják a metszéspontok különbözőségét, viszont sok metszéspont akkor keletkezik, ha egy-egy szakaszt minél több másik metsz. Erre utal az I. megoldáshoz fűzött 2. megjegyzés is.
Másfelől talán az is váratlan első pillanatra, hogy 7 pont még nem föltétlenül teszi lehetővé 2 metszéspontot létrehozó, közös végpont nélküli szakaszok kiválasztását. Erre a 8. ábra két példát is mutat.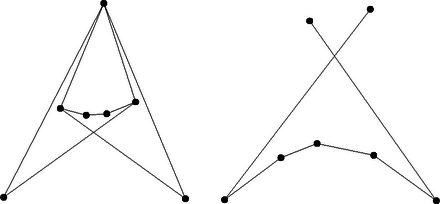
 
 

8. ábra
 

A megoldások 9 pont esetén biztosítják 2 metszéspont létrehozását. A lehetséges esetek megfelelő csoportosításával és végigvizsgálásával belátható, hogy már 8 pont közül is mindig kiválaszthatók 2 különböző metszéspontot szolgáltató, közös végpont nélküli szakaszok végpontjai.
Ebből következik, hogy 5 metszéspont létrehozására már 20 pont is elegendő és általában n metszéspont létrehozására 4n pont. Valóban, 3 ‐ általában n-2 ‐ metszéspont létrehozására alkalmazhatjuk bármelyik megoldás eljárását, és az utolsó 8 pont közül kiválaszthatók még további 2 metszéspontot adó szakaszok végpontjai.
Az elmondottak részleteire és további megjegyzésekre külön cikkben térek vissza.
 
Harmadik feladat. Van 30 perselyünk és mindegyikhez egy-egy kulcsunk, amely a többi perselyt nem nyitja. Valaki találomra bedobja a bezárt perselyekbe a kulcsokat, mindegyikbe egyet. Két perselyt feltörünk. Mi annak a valószínűsége, hogy a többit további perselyek feltörése nélkül ki tudjuk nyitni?
 
I. megoldás. Mielőtt a felnyitáshoz kezdenénk, rakjuk sorba a perselyeket azzal a kettővel kezdve, amelyeket majd feltörünk és írjuk rájuk a sorszámukat.
Miután találomra dobták be a kulcsokat a perselyekbe, és a feltörni szánt két perselyt is csak találomra tudjuk kiválasztani, így egyenlő eséllyel jöhet létre a kulcsok minden elrendezése a perselyekben.
Most feltörjük az első két perselyt. Ha az első perselyben nem a saját kulcsa volt, akkor a benne található kulccsal kinyitjuk azt a perselyt, amelyiket nyitja, kivesszük a benne található kulcsot és a perselyt félreállítjuk. Az újabb kulccsal kinyitjuk a megfelelő perselyt, kivesszük belőle a kulcsot és a perselyt az előbbi mellé állítjuk, és így haladunk tovább, amíg lehet.
Ha közben előkerül a második persely kulcsa is, úgy járunk el, mintha azt fel sem törtük volna, kivesszük abból is a kulcsot és a perselyt a nyitott perselyek sorába állítjuk.
Akkor akadunk meg, amikor az első persely kulcsa kerül elő és ez lehet mindjárt akkor is, amikor az első perselyből vesszük ki a benne levő kulcsot. Világos, hogy más nyitott persely kulcsa nem kerülhet elő, mert az már korábban előkerült, és egy perselynek csak egy kulcsa van.
Amikor az első persely kulcsa kerül elő, akkor az első perselyt is áttesszük a felnyitott perselyek sorába. Ezután kivesszük a második perselyben levő kulcsot, ha még nem került elő, és folytatjuk az eljárást. Ez befejeződik, ha a második persely kulcsa is előkerült.
Ha még nem nyitottunk ki közben minden perselyt, ez a kérdezett valószínűség szempontjából kedvezőtlen eset. Ekkor is folytassuk az eljárást úgy, hogy valahányszor elakadunk, mindig feltörjük az első még ki nem nyitott perselyt.
Ilyen módon minden kulcselosztáshoz a perselyekben hozzárendeltük a (nyitott) perselyeknek egy sorrendjét. Fordítva, a perselyelrendezést ismerve mindegyikbe vissza tudjuk tenni azt a kulcsot, amelyik abba volt bedobva. Az első helyen álló persely kulcsát kell az 1-es sorszámú perselybe tenni, ezután az első sorszámú perselyig mindegyiknek a kulcsát az előtte álló perselybe. Az 1-es sorszámú persely után álló persely kulcsa a legkisebb sorszámú még üres perselybe kerül, az addig álló perselyek kulcsa az előttük levő perselybe és így tovább.
A perselyek elrendezése akkor tartozik a kulcsok egy kedvező sorrendjéhez, ha az utolsó helyen az 1-es vagy 2-es sorszámú persely áll, különben kedvezőtlen kulcs-sorrendhez tartozik. Bármelyik persely áll is az utolsó helyen, az előtte állókat mindig ugyanannyiféleképpen lehet elrendezni, így az, hogy az utolsó helyen egy-egy megadott persely áll, csupa egyenlő valószínűségű esemény, összesen 30. Ezek közül 2 kedvező, tehát a keresett valószínűség 1/15.
Világos, hogy általában, ha n persely van és közülük k-t törünk fel (k≤n), akkor k/n a valószínűsége annak, hogy mindegyik perselyt ki tudjuk nyitni.
 
Megjegyzés. A versenyzők nagy része összeszámolta az összes és a kedvező kulcselosztásokat, részben úgy, hogy a feltörésre szánt perselyek kiválasztását is az eseményekhez számította. A kedvező események összeszámolását többen azzal könnyítették meg, hogy minden olyan elrendezéshez, amelyben lényeges volt a második persely feltörése is, hozzápárosítottak kölcsönösen egyértelműen egy olyant, amelyben a második persely feltörése nélkül is már mind kinyitható. Ilyent kapunk, ha az első persely kulcsát tesszük abba a perselybe, amelyikben a másodiké volt és viszont.
 
II. megoldás. Azt fogjuk bizonyítani, hogy ha n perselybe dobjuk be kulcsaikat találomra és kettőt feltörünk közülük, akkor 2/n annak a valószínűsége, hogy minden perselyt ki tudjunk nyitni.
Jelöljük a keresett valószínűséget pn-nel. Természetesen p2=1. Megmutatjuk, hogy ha n≥2, akkor
pn+1=nn+1pn.(1)
Ebből már következik, hogy
pn=n-1n⋅n-2n-1⋅...⋅23⋅p2=2n,
és a feladat esetére p30=1/15.
Tekintsük az n+1 kulcsnak egy E elhelyezését a perselyekben. Jelölje r annak a perselynek a sorszámát, amelyikben az (n+1)-edik persely kulcsa van és s azét, amelyiknek a kulcsa az (n+1)-edikben van. Világos, hogy vagy r is és s is (n+1)-gyel egyenlő (az utolsó persely a saját kulcsát tartalmazza), vagy mindkettő kisebb, mint n+1.
Az előbbi esetben az n+1-edik perselyt figyelmen kívül hagyva kapjuk az első n persely kulcsainak egy E1 elhelyezését az első n perselyben. Az utóbbiban is hozzárendelünk E-hez egy ilyen E1 elrendezést, azt, amelyik annyiban különbözik csak E-től, hogy az r-edik perselybe az s-edik kulcsát dobjuk.
Ilyen módon minden E-hez rendeltünk egy E1-et. Megfordítva, ha E1-et ismerjük, ez keletkezhetett E-ből úgy, hogy az első, vagy a második, vagy ..., vagy az n-edik perselyből vettük ki az (n+1)-edik persely kulcsát és cseréltük ki az (n+1)-edikben levő kulccsal vagy úgy, hogy figyelmen kívül hagytuk az (n+1)-edik perselyt, amelyikben a saját kulcsa volt. Így az n kulcs egy E1, elhelyezése az n+1 kulcs (n+1)-féle különböző elhelyezéséhez van hozzárendelve.
Ha most az első 2 perselyt feltörjük, akkor E-ben és E1-ben ugyanazokat a perselyeket tudjuk kinyitni, amíg csak el nem jutunk az r-edikhez. Ha ez bekövetkezik, akkor E-ben felnyithatóvá válik az (n+1)-edik persely, majd azt felnyitva az s-edik, E1-ben pedig közvetlenül az s-edik. Tovább ismét mind a két kulcselhelyezés esetén ugyanazok a perselyek nyithatók ki.
Akkor és csak akkor nyitható tehát fel az E kulcselhelyezés esetén mind az n+1 persely, ha a hozzárendelt E1 kulcselhelyezéssel az első n persely felnyitható és az (n+1)-edik perselyben nem a saját kulcsa van.
Ezek szerint az n kulcs minden lehetséges elhelyezéséhez az n+1 kulcs n+1 elhelyezése tartozik és minden olyan elhelyezéshez, amiben az összes persely felnyitható, az n+1 persely kulcsainak n ilyen elhelyezése. Ez éppen az (1) összefüggést szolgáltatja.
 
Megjegyzés. Ugyanígy látható, hogy akkor is fennáll (1), ha pn annak a valószínűsége, hogy k persely feltörése esetén minden persely kinyithatóvá válik. Mivel ekkor pk=1, így ismét adódik, hogy ebben az általánosabb esetben pn=k/n.