Kezdőlap


Cím:	Sztatikai feladatok megoldása II.
Szerző(k):	Mihály László
Füzet:	1971/november, 169 - 173. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Sztatikai feladatok megoldása II. ^{$^{*}$}

A forgatónyomaték fogalmának megértéséhez képzeljük el, hogy valaki egy hosszú rudat tart egyik végénél fogva. Ha a rúdra súlyt akasztunk, akkor a kifejtendő hatás nemcsak a súly nagyságától, hanem a súly és a kezünk közti távolságtól is függ; minél messzebb rakjuk a terhelést, annál erősebben kell tartani a rudat. Persze mindez csak akkor van így, ha az erő nem a rúd irányába mutat. Ha a rudat függőlegesen (lefelé) tartjuk, akkor teljesen mindegy, hogy hova akasztjuk a súlyt. Ennek alapján jogos bevezetni egy új mennyiséget az

\begin{matrix} M = F \cdot r \cdot sin α \end{matrix}

egyenlőséggel. Ezt a számot az

F

erőnek a tőle

r

távolságban levő ponton átmenő, az

F

és az

r

síkjára merőleges tengelyre vonatkozó forgatónyomatékának nevezzük (11. ábra).

α

az erő és helyvektor egymással bezárt szöge.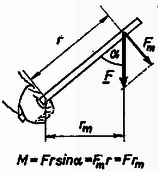

11. ábra

Természetesen a fenti szemléltetés nem indokolja, miért pont ezt a mennyiséget neveztük forgatónyomatéknak. Végeredményben az a döntő, hogy a (2) egyenletbe ennek alapján behelyettesített mennyiségekkel az egyenletrendszer a valósággal egyező eredményt ad.
Az egyenletet megfelelően átrendezve láthatjuk, hogy

\begin{matrix} M = F \cdot (r \cdot sin α) = F \cdot r_{m}, \\ M = (F \cdot sin α) \cdot r = F_{m} r, \end{matrix}

ahol

r_{m}

a forgástengelynek és az erő hatásvonalának távolsága,

F_{m}

F

erő a támadáspontot a forgástengellyel összekötő egyenesre merőleges komponensének a nagysága. A gyakorlatban általában az utóbbi két egyenlőség valamelyikét használjuk.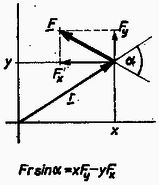

2. ábra

A definíció alapján könnyen bizonyítható az is, hogy a 12. ábra szerinti derékszögű koordináta-rendszert választva

\begin{matrix} M = x F_{y} - y F_{x} . \end{matrix}

(Ez egyébként nyilvánvalóvá válik, ha az

F

erőt komponenseivel helyettesítjük, és azok forgatónyomatékát külön-külön számoljuk, majd összegezzük.)
Láthatjuk továbbá, hogy a forgatónyomatékok szempontjából nagyon fontos, hogy hol van az erő támadáspontja. Az erővektorokat nem mozgathatjuk tetszőlegesen; a forgatónyomaték csak akkor nem változik, ha az erőt hatásvonalában toljuk el.
A forgatónyomatékot mindig valamilyen (képzeletbeli vagy valóságos) forgástengelyre vonatkoztatjuk. Nagyon érdekes tény, hogy ha teljesül a (1) egyenlőség, azaz a testre ható erők eredője nulla, akkor teljesen mindegy, hogy a testre ható erők forgatónyomatékát melyik tengelyre vonatkoztatjuk, mert mindenképpen ugyanazt az értéket kapjuk.
Legyenek a testre ható erők:

F_{1}, F_{2}, ..., F_{n}

. Ha az

i

-edik erőt

F_{i}

-vel, támadáspontjának koordinátáit

x_{i}

-vel és

y_{i}

-vel jelöljük, akkor ezen erő forgatónyomatéka a koordináta-rendszer kezdőpontján áthaladó tengelyre:

\begin{matrix} M_{i} = x_{i} F_{i y} - y_{i} F_{i x} . \end{matrix}

E tengelyre tehát összesen

\begin{matrix} M = M_{1} + M_{2} + ... + M_{n} = (x_{1} F_{1 y} - y_{1} F_{1 x}) + (x_{2} F_{2 y} - y_{2} F_{2 x}) + ... + (x_{n} F_{n y} - y_{n} F_{n x}) \end{matrix}

forgatónyomaték hat.
Számítsuk ki, mekkora nyomaték forgat egy olyan tengely körül, amely az

x_{0}

y_{0}

ponton halad keresztül ! Az

i

-edik erő nyomatéka ekkor

\begin{matrix} M'_{i} = (x_{i} - x_{0}) F_{i y} - (y_{i} - y_{0}) F_{i x}, \end{matrix}

mert megváltozik az erő támadáspontja és a forgástengely közötti távolság. Átrendezve:

\begin{matrix} M'_{i} = (x_{i} F_{i y} - y_{i} F_{i x}) - x_{0} F_{i y} + y_{0} F_{i x} = M_{i} - x_{0} F_{i y} + y_{0} F_{i x} . \end{matrix}

Az összes nyomaték:

\begin{matrix} M' = M'_{1} + M'_{2} + ... + M'_{n} = (M_{1} - x_{0} F_{1 y} + y_{0} F_{1 x}) + (M_{2} - x_{0} F_{2 y} + y_{0} F_{2 x}) + \\ + ... (M_{n} - x_{0} F_{n y} + y_{0} F_{n x}) . \end{matrix}

Az összeget megfelelően rendezzük,

x_{0}

-t,

y_{0}

t kiemeljük:

\begin{matrix} M' = M_{1} + M_{2} + ... M_{n} - x_{0} (F_{1 y} + F_{2 y} + ... + F_{n y}) + y_{0} (F_{1 x} + F_{2 x} + ... + F_{n x}) . \end{matrix}

Amennyiben a testre ható erők eredője nulla, akkor

\begin{matrix} F_{1 x} + F_{2 x} + ... + F_{n x} & = 0, \\ F_{1 y} + F_{2 y} + ... + F_{n y} & = 0, így \\ M' = M_{1} + M_{2} + ... M_{n} & = M, \end{matrix}

azaz a forgatónyomaték nem változik.
E bizonyításnak egy speciális esete az, amikor kiszámoljuk, hogy az erőpár forgatónyomatéka bármely tengelyre ugyanakkora. Ebből következik az is, hogy a (2) egyenletet tetszőleges tengelyre felírhatjuk.
Eddig csak olyan esetekkel foglalkoztunk, amikor a vizsgált testre ható erők egy síkban voltak; a forgástengelyt úgy választottuk, hogy az erre a síkra merőleges legyen. Térbeli problémánál a kiválasztott tengely körüli forgatónyomatékot úgy kell meghatározni, hogy a testre ható erőket egy, a tengelyre merőleges síkra vetítjük, és a vetületek nyomatékával számolunk. (Később ez az eljárás vezet arra, hogy a forgatónyomatékot is mint vektormennyiséget definiáljuk az

M = F \times r

vektoriális szorzattal. A fenti módszerrel tulajdonképpen az

M

vektornak az adott tengely irányába eső vetületét kapjuk meg.)
Mint a 2. feladat megoldásánál is láthattuk, az egyszerűbb problémáknál a (2) egyenletet nem kell felhasználni. Nézzük most a cikk első részében közölt 1. feladatot !
A megoldáshoz a 3. ábrán látható szétbontást alkalmazzuk. Az erőket vízszintes és függőleges komponensükkel (

x

, illetve

y

index) helyettesítjük. Az egyenletek felírása előtt pozitív irányt választunk; az ezzel ellentétesen mutató komponensek negatív előjelet kapnak. Kijelöljük a pozitív forgásirányt is.
A vízszintes rúdra az (1) egyenletből:

\begin{matrix} - A_{x} + C_{x} & = 0, \\ A_{y} - G_{1} + C_{y} - G & = 0. \end{matrix}

A forgatónyomatékokat az

A

pontra írjuk fel, mert ezen egy ismeretlen erő hatásvonala keresztülhalad, és így ez az erő az egyenletben nem fog szerepelni:

\begin{matrix} G_{1} \cdot \frac{l}{2} - C_{y} \cdot l \cdot sin α + G \cdot l = 0. \end{matrix}

Ehhez hasonlóan a ferde rúdra:

\begin{matrix} B_{x} - C'_{x} = 0, B_{y} - G_{2} - C'_{y} = 0. \end{matrix}

A forgatónyomatékok a

B

pontra:

\begin{matrix} G_{2} \cdot \frac{l}{2} \cdot sin α + C_{y} \cdot l \cdot sin α - C_{x} \cdot l \cdot cos α = 0. \end{matrix}

Egyenletrendszerünkben ismeretlenek az

A

B

C

C'

erők függőleges és vízszintes komponensei, összesen

8

ismeretlen. A megoldhatósághoz szükséges további két egyenletet a (3) összefüggésből kapjuk meg:

\begin{matrix} C_{x} = C'_{x}, C_{y} = C'_{y} . \end{matrix}

(Azt, hogy az erők ellentétes irányúak, a berajzoláskor figyelembe vettük.) Ez az egyenletrendszer már megoldható; végeredményben

\begin{matrix} A_{x} = B_{x} = C_{x} = \frac{(G_{2} / 2) \cdot sin α + (G_{1} / 2) + G}{cos α}, \\ A_{y} = \frac{G_{1} (sin α - l / 2) - G (1 - sin α)}{sin α}, \\ B_{y} = \frac{(G_{1} / 2) + G}{sin α} + G_{2} C_{y} = \frac{(G_{1} / 2) + G}{sin α} . \end{matrix}

Ha a megadott számértékeket behelyettesítjük, megkapjuk a keresett erőket. (Végezzük el a behelyettesítést

G_{1} = G_{2} = 60

kp,

G = 30

kp,

α = 45^{\circ}

mellett, és határozzuk meg az erőket nagyság és irány szerint !)
Természetesen ugyanerre az eredményre jutunk, ha valamilyen ötletes módon elkerüljük a nyolcismeretlenes egyenletrendszer megoldását. (Például először a 2. ábra szerinti szerkezetet vizsgálva, meghatározzuk

A

-t és

B

-t, utána a ferde rúd egyensúlyi feltételéből kiszámítjuk

C

-t.) A fenti módszer azonban teljesen általános, alkalmazása semmilyen különleges ötletet nem igényel.
Ha a 4. ábra szerinti darabolást alkalmazzuk, akkor azt is megkapjuk, hogy az egyes rudakban mekkora erők hatnak. A rúdban ható erő értelemszerűen az az erő, amellyel a rúdnak képzeletben eltávolított egyik részét helyettesítjük. A rúdban ható erő kiszámolásánál tehát azt kell felhasználni, hogy a megmaradt rész egyensúlyban van, ezért az elhagyott rész reá pontosan akkora erővel (és forgatónyomatékkal) hat, hogy az kiegyenlítse a külső hatásokat. Ehhez hasonlóan definiálhatjuk a rúdban ható forgatónyomatékot is. (Lásd még: a K. M. L. 1970. évi 4. szám 860. feladat megoldását.) A 13. ábrán láthatjuk egy tartó egyes keresztmetszetein ható erőket és forgatónyomatékokat (

| N_{x} |

| N_{y} |

az erő vetületei).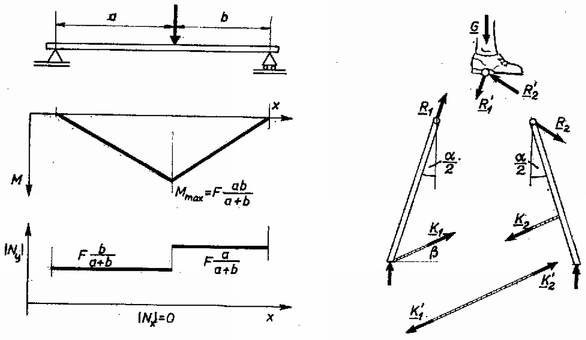

13. ábra 14. ábra

A valóságban a rúdban ható erő mérésére a rúd deformációit használjuk fel. Ha a rúd megnyúlik, húzóerőt, ha egyes keresztmetszetei elcsúsznak egymáson (mint a kártyalapok), akkor rúdra merőleges, ún. nyíróerőt továbbít. Ha a rúd meghajlik, akkor forgatónyomatékot ad át.
Vannak feladatok, amelyek megoldása jelentősen egyszerűsödik, ha felhasználjuk a problémában található szimmetriákat. (Egy ilyen szimmetria-tulajdonság felhasználása egy forgatónyomatéki egyenlettel ekvivalens.) Óvatosnak kell lenni azonban, mert a helytelenül alkalmazott szimmetria-meggondolások nagyon nehezen felderíthető hibákra vezetnek. (Az itt elkövethető hibák tanulmányozására oldjuk meg a következő feladatot.

α

csúcsszögű létra áll súrlódásmentes síkon. A létra szárait egy, a vízszintessel

β \neq 0

szöget bezáró kötél köti össze, amely az egyik szár aljából indul ki. Mekkora erő feszíti a kötelet, ha a létra tetején

G

súlyú ember áll ? A 14. ábrán berajzoltuk a javasolt darabolást, és az egyes részekre ható erőket, ennek alapján megkezdhetjük a megoldást.)
Végül előfordulhatnak olyan esetek, amikor az itt tanult módszerrel nem tudjuk a feladatot megoldani. Ezek az úgynevezett sztatikailag határozatlan szerkezetek.
Sztatikailag határozatlan egy olyan szerkezet, amelyben vannak olyan pontok, amelyek helye geometriailag túlhatározott. Határozatlan lesz például az 1. ábrán látható tartó, ha a

C

pontban a két rudat mereven összekötjük, mert ekkor az

A

és

B

pontok távolságát nemcsak a falra szerelt csuklók határozzák meg. Ha a csuklók távolsága csak egy kicsit is eltér a megszabottól, ismeretlen nagyságú feszítő erők lépnek fel. Ezt és az ehhez hasonló buktatókat általában elkerülhetjük, ha feltesszük, hogy a vizsgált feladatban a rudakat csuklók kötik össze.
A sztatikailag határozatlan feladat egyből határozottabbá válik, ha a rudakat nem tekintjük merevnek, a köteleket nyújthatatlannak. Ez azonban már a rugalmasságtan ‐ matematikailag bonyolultabb, fizikailag mélyebb tartalmú ‐ egyenleteihez vezet.

Javasolt irodalom: Feynman: Mai fizika 1., K. M. L. 1970. 4. sz. 860., 1971. 2. sz. 914., 1971. 3. sz. 921., 1971. 4. sz. 939. feladat megoldása. Vermes Miklós: Fizikai versenyfeladatok II.

^{$^{*}$}A cikk első részét l. a szeptemberi számban. Ugyanott a 35. oldal negyedik bekezdésének utolsó sora helyesen: ,,... általa kifejtett erővel és forgatónyomatékkal helyettesíthetjük.'' Ennek megfelelően kiegészítendő a 4. ábra.