Kezdőlap


Cím:	Az 1971. évi (5.) Nemzetközi Fizikai Diákolimpia feladatai
Szerző(k):	Gács Lajos , Iglói Ferenc , Mosó Tamás , Szabó Zoltán , Tichy-Rács Ádám
Füzet:	1971/november, 161 - 168. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Vízszintes síkra helyezett $m$ tömegű ék (kettős lejtő) tetején átvetett fonálon $m_{1}$ és $m_{2}$ tömegek lógnak. A lejtők hajlásszögei $α_{1}$ és $α_{2}$ (1. ábra). A súrlódás, a fonál és a csiga tömege elhanyagolható. Kezdetben az egész rendszer nyugalomban van, azután elengedjük. Mennyi az ék gyorsulása ? Mennyi a fonálon lógó testek gyorsulása ? Mikor marad az ék nyugalomban ?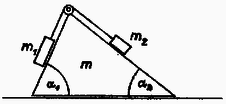

1. ábra

Megoldás. Minden gyorsulást az inerciarendszerhez képest számítunk. Az ék gyorsulása

a

, a testek gyorsulása a lejtőhöz képest

a_{0}

. A lógó tömegek gyorsulása az inerciarendszerhez képest

a_{0}

és

a

nagyságú vektorok eredője (

a_{1}

, illetve

a_{2}

). Az irányokat a 2. ábrán feltüntetett esetben számítjuk pozitívoknak.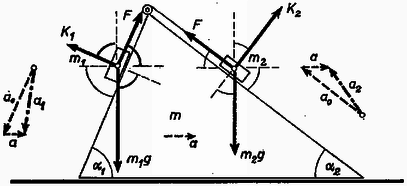

2. ábra

m_{1}

tömegre

m_{1} g

súlya, a lejtő részéről merőlegesen kifejtett

K_{1}

erő és

F

fonálerő hat. Ezek vektoreredője adja az

m_{1} a_{1}

mozgató erőt. Hasonló a helyzet

m_{2}

-nél. Az éket mozgató

m a

erőt

K_{1}

K_{2}

, ill. a két

F

nagyságú reakcióerő vízszintes összetevőinek összege adja. Ezeket az összefüggéseket függőleges és vízszintes összetevőkben felírva 5 egyenletet kapunk az 5 ismeretlen (

a_{0}

a

K_{1}

K_{2}

F

) számára. Az egyenletrendszer megoldása hosszadalmas.
Célszerű, ha Newton II. axiómáját a lejtőmenti erőösszetevőkre írjuk fel.

K_{1}

és

K_{2}

lejtőre merőleges erők most nem játszanak szerepet.

m_{1}

tömeget a lejtő mentén lefelé (a választott pozitív irányban)

m_{1} g sin α_{1} - F

erő mozgatja. Az

m_{1}

tömeg inerciarendszerhez képest számított gyorsulásának lejtőmenti összetevője

a_{0} - a cos α_{1}

. Az erőtörvény szerint:

\begin{matrix} m_{1} (a_{0} - a cos α_{1}) = m_{1} g sin α_{1} - F, \end{matrix}

innen a fonálerő:

\begin{matrix} F = m_{1} (g sin α_{1} + a cos α_{1} - a_{0}) . \end{matrix}

(1)

Hasonlóan

m_{2}

tömegnél:

\begin{matrix} m_{2} (a_{0} - a cos α_{2}) = F - m_{2} g sin α_{2}, \end{matrix}

ebből:

\begin{matrix} F = m_{2} (g sin α_{2} - a cos α_{2} + a_{0}) . \end{matrix}

(2)

A fonálerő (1) és (2) kifejezéseit egyenlővé téve:

\begin{matrix} (m_{1} cos α_{1} + m_{2} cos α_{2}) a = (m_{1} + m_{2}) a_{0} - (m_{1} sin α_{1} - m_{2} sin α_{2}) g . \end{matrix}

(3)

Az ék viselkedésére legegyszerűbben az impulzustörvényből következtethetünk. A lógó tömegek lejtőhöz viszonyított sebességei

v_{0}

(bal oldalt lefelé, jobb oldalt felfelé), ezek vízszintes összetevői

v_{0} cos α_{1}

és

v_{0} cos α_{2}

(balra). Figyelembe véve az ék jobbra mutató

v

sebességét, a lógó tömegek sebességösszetevői az inerciarendszerhez képest

v_{0} cos α_{1} - v

és

v_{0} cos α_{2} - v

. Az impulzustétel szerint:

\begin{matrix} m_{1} (v_{0} cos α_{1} - v) + m_{2} (v_{0} cos α_{2} - v) = m v . \end{matrix}

Egyenletesen gyorsuló mozgásról lévén szó a sebességek arányosak a gyorsulásokkal, ezért

\begin{matrix} m_{1} (a_{0} cos α_{1} - a) + m_{2} (a_{0} cos α_{2} - a) = m a . \end{matrix}

Rendezve:

\begin{matrix} a = \frac{m_{1} cos α_{1} + m_{2} cos α_{2}}{m + m_{1} + m_{2}} \cdot a_{0} . \end{matrix}

(4)

Ez az összefüggés mutatja, hogyha a két gyorsulás közül az egyik nulla, akkor a másik is az. Az ék csak akkor maradhat nyugalomban, ha a lógó tömegek is nyugosznak rajta. Ami különben azonnal belátható az impulzustörvényből.
A (3)-ból és (4)-ből álló egyenletrendszer megoldása

a_{0}

és

a

gyorsulásokra ezeket az eredményeket adja:

\begin{matrix} a_{0} = g \cdot \frac{(m + m_{1} + m_{2}) (m_{1} sin α_{1} - m_{2} sin α_{2})}{(m_{1} + m_{2}) (m + m_{1} + m_{2}) - {(m_{1} cos α_{1} + m_{2} cos α_{2})}^{2}}, & (5) \\ a = g \cdot \frac{(m_{1} cos α_{1} + m_{2} cos α_{2}) (m_{1} sin α_{1} - m_{2} sin α_{2})}{(m_{1} + m_{2}) (m + m_{1} + m_{2}) - {(m_{1} cos α_{1} + m_{2} cos α_{2})}^{2}} . & (6) \end{matrix}

Mindkét gyorsulás akkor nulla, ha

\begin{matrix} \frac{m_{1}}{m_{2}} = \frac{sin α_{2}}{sin α_{1}} . \end{matrix}

A fonálerő kiszámítására (1)-et és (2)-t összeadjuk; felhasználva az (5) és (6) szerinti eredményeket:

\begin{matrix} F = g m_{1} m_{2} \cdot \frac{(m + m_{1} + m_{2}) (sin α_{1} + sin α_{2}) - (m_{1} cos α_{1} + m_{2} cos α_{2}) \cdot sin (α_{1} + α_{2})}{(m_{1} + m_{2}) (m + m_{1} + m_{2}) - {(m_{1} cos α_{1} + m_{2} cos α_{2})}^{2}} . \end{matrix}

K_{1}

és

K_{2}

kényszererők kiszámításához

m_{1}

és

m_{2}

tömegeknél a függőleges erő-összetevőket vesszük számításba:

\begin{matrix} m_{1} a_{0} sin α_{1} = m_{1} g - K_{1} cos α_{1} - F sin α_{1}, \\ m_{2} a_{0} sin α_{2} = - m_{2} g + K_{2} cos α_{2} + F sin α_{2} . \end{matrix}

Ezekből az egyenletekből, (1), (2), (6) felhasználásával:

\begin{matrix} K_{1} = m_{1} g cos α_{1} [1 - \frac{tg α_{1} (m_{1} cos α_{1} + m_{2} cos α_{2}) (m_{1} sin α_{1} - m_{2} sin α_{2})}{(m_{1} + m_{2}) (m + m_{1} + m_{2}) - {(m_{1} cos α_{1} + m_{2} cos α_{2})}^{2}}], \\ K_{2} = m_{2} g cos α_{2} [1 + \frac{tg α_{2} (m_{1} cos α_{1} + m_{2} cos α_{2}) (m_{1} sin α_{1} - m_{2} sin α_{2})}{(m_{1} + m_{2}) (m + m_{1} + m_{2}) - {(m_{1} cos α_{1} + m_{2} cos α_{2})}^{2}}] . \end{matrix}

Valamennyi képletünkból a rögzített ék esete az

m = \infty

helyettesítéssel kapható meg.
Egy konkrét példa feladatunkra:

\begin{matrix} \begin{matrix} a_{1} = 67, 4^{\circ}, & sin α_{1} = 12 / 13, & cos α_{1} = 5 / 13, \\ a_{2} = 36, 9^{\circ}, & sin α_{2} = 3 / 5, & cos α_{2} = 4 / 5, \end{matrix} \end{matrix}

m = 20 kg, m_{1} = 13 kg, m_{2} = 10 kg

.
Ekkor

a_{0} = \frac{129}{410} \cdot g = 0, 315 g, a = \frac{39}{410} \cdot g = 0, 095 g

F = \frac{1719 kg}{205} \cdot g = 82, 3 newton, K_{1} = \frac{791 kg}{205} \cdot g = 37, 9 newton, K_{2} = \frac{1757 kg}{205} \cdot g = 84, 1 newton

Mosó Tamás

2. Dugattyús hengerben Torricelli-kísérlet van összeállítva (3. ábra), a higany fölött hidrogén, a hengerben levegő van. Az 1. állapotban a higanyoszlop magassága

70 cm

, a levegő nyomása

p_{l 1} = 1, 334 \cdot 10^{5} N/m^{2}=1,317

atmoszféra

= 100 Hgcm

, a hőmérséklet

0^{\circ} C = 273^{\circ} K

. A dugattyút állandó hőmérséklet mellett lassan felhúzva a levegő nyomása a 2. állapotban

p_{l 2} = 0, 8 \cdot 10^{5} {N/m}^{2} = 0, 79

atmoszféra

= 60 Hgcm

lesz és a higanyszint

40 cm

. Ezután a dugattyú változatlan helyzete mellett a hőmérsékletet

T_{3}

fokra emeljük; ebben a 3. állapotban a higanyoszlop magassága

50 cm

. Végül úgy jutunk a 4. állapothoz, hogy a levegő nyomása változatlan marad, de a higanyszál magassága

45 cm

lesz. Mennyi a hidrogéngáz nyomása és hőmérséklete a végső állapotban ?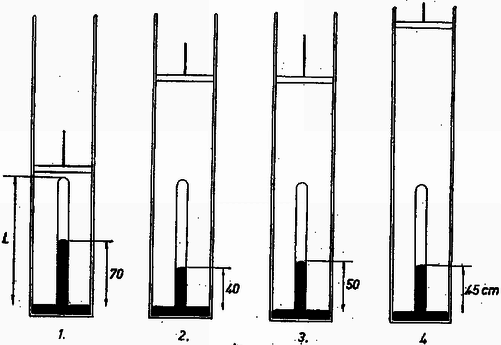

3. ábra

Megoldás. A hidrogén és a levegő adatait a négy állapotban következőképp jelöljük:

\begin{matrix} 1. & 2. & 3. & 4. \\ hidrogén nyomása & p_{h 1} & p_{h 2} & p_{h 3} & p_{h 4} \\ hidrogén térfogata & V_{h 1} & V_{h 2} & V_{h 3} & V_{h 4} \\ levegő nyomása & p_{l 1}=100 Hg cm & p_{l 2}=60 Hg cm & p_{l 34} = & = p_{l 34} \\ levegő térfogata & V_{l 1} & V_{l 23} = & = V_{l 23} & V_{l 4} \\ közös hőmérséklet & 273^{\circ} K & 273^{\circ} K & T_{3} & T_{4} \end{matrix}

Minden nyomást Hgcm-ben mérünk. A Torricelli-cső hossza

L

(cm-ben), a hidrogén térfogatának mértéke, a hidrogén által betöltött csőrész hossza.
A hidrogénre az 1. és 2. állapotok között alkalmazzuk Boyle‐Mariotte törvényét. A nyomások

p_{h 1} = (100 - 70) Hgcm=30 Hgcm

és

p_{h 2} = (60 - 40) Hgcm=20Hgcm

. Tehát

\begin{matrix} 30 (L - 70) = 20 (L - 40) . \end{matrix}

Innen megtudjuk a Torricelli-cső hosszát:

L = 130 cm

. A négy hidrogéntérfogatnak megfelelő csőhossz:

\begin{matrix} (V_{h 1}) 60 cm, (V_{h 2}) 90 cm, (V_{h 3}) 80 cm, (V_{h 4}) 85 cm . \end{matrix}

A hidrogén nyomása a 3., illetve 4. állapotban

p_{l 3} = p_{h 34} - 50 Hgcm

, illetve

p_{h 4} = p_{l 34} - 45 Hgcm

. A levegő nyomása 3. és 4. között nem változott meg, ezért a higanyszál csak úgy mehetett le, hogy a hőmérséklet emelkedett. De akkor a dugattyút is feljebb kell húzni, hogy melegebb állapotban a levegő nyomása ugyanannyi maradhasson.
Felírjuk a hidrogénre az egyesített gáztörvényt a 2. és 3. állapotok között:

\begin{matrix} \frac{20 \cdot 90}{273} = \frac{(p_{l 34} - 50) 80}{T_{3}} . \end{matrix}

Felírjuk a hidrogénre az egyesített gáztörvényt a 3. és 4. állapotok között:

\begin{matrix} \frac{(p_{l 34} - 50) 80}{T_{3}} = \frac{(p_{l 34} - 45) 85}{T_{4}} . \end{matrix}

Felírjuk a levegőre Gay-Lussac II. törvényét a 2. és 4. állapotok között:

\begin{matrix} \frac{p_{l 34}}{60} = \frac{T_{3}}{273} . \end{matrix}

Ennek az egyenletrendszernek a megoldása:

p_{l 34} = 80 Hgcm

T_{3} = 364^{\circ} K

T_{4} = 451^{\circ} K

. A hidrogén nyomásai:

p_{h 3} = 30 Hgcm

p_{h 4} = 35 Hgcm

. Ezzel minden kérdésre feleltünk.
A levegő térfogatainak az arányát is kiszámíthatjuk:

\begin{matrix} V_{l 1} : V_{l 23} : V_{l 4} = 6 : 10 : 12, 4. \end{matrix}

Ha ismeretes, hogy a Torricelli-cső keresztmetszet-területe például

2 cm^{2}

, akkor az első állapotban a hidrogén térfogata

2 \cdot 60 {cm}^{3} = 120 {cm}^{3}

30

Hgcm nyomás mellett,

273^{\circ} K

-en. Ezért hidrogénünk normáltérfogata

(120 \cdot 30 : 76) {cm}^{3} = 47, 37 {cm}^{3}

. Mivel

22 400 {cm}^{3}

normálállapotú hidrogén tömege

2, 016

gramm, ezért a mi hidrogénünk tömege

(47, 37 \cdot 2, 016 : 22 400) gramm = 0, 00426 gramm

Iglói Ferenc

Megjegyzés. Az eredeti feladat figyelembe kívánta vetetni a higany hőkiterjedését is. Fizikus szempontból nézve ennek nincs sok értelme, hiszen a higany nem-lineáris hőkiterjedése és gőznyomása legalább annyit jelent, mint a hőkiterjedés okozta százalékos nagyságrendi eltérés.

3. A 4. ábra bal oldali rajza szerinti kapcsolásban

R

négy darab egyenlő ellenállást,

C_{1}

C_{2}

C_{3}

C_{4}

egyenlő,

1 μ F

-os kondenzátort jelent. A négy áramforrás feszültségei

U_{1} = 4 volt

U_{2} = 8 volt

U_{3} = 12 volt

és

U_{4} = 16 volt

; belső ellenáldásuk elhanyagolható. Mennyi a négy kondenzátor összes energiája ? Mennyi a

C_{2}

kondenzátor töltése, ha

H

és

B

pontokat rövidre zárjuk ?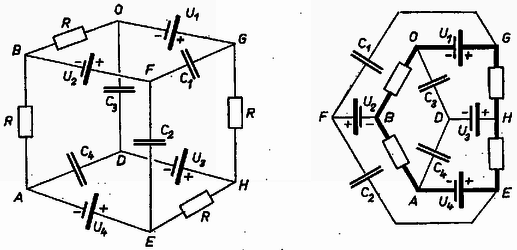

4. ábra

Megoldás. A kondenzátor

C U

töltésének és

C U^{2} / 2

energiájának a kiszámításához a feszültségre van szükségünk. Terítsük ki a hálózatot síkba (4. ábra jobb oldali rajza). Az egyenáram nem folyhat át kondenzátorokon, ezért csak az ábra vastagon rajzolt vezetékein folyik áram. Ebben az áramkörben

4 R

ellenállásra

U_{4} - U_{1} = 12

volt feszültség van rákapcsolva, tehát az áramerősség:

\begin{matrix} I = \frac{U_{4} - U_{1}}{4 R} . \end{matrix}

Az ohmos feszültségesések és a telepek feszültségeinek a felhasználásával kiszámítjuk az egyes pontok feszültségeit, alapul választva

A

pont feszültségét mint nullát.

\begin{matrix} A & 0 volt \\ B(U_{4} - U_{1}) / 4 & 3 volt \\ O(U_{4} - U_{1}) / 2 & 6 volt \\ G(U_{4} - U_{1}) / 2 + U_{1} & 10 volt \\ H(U_{4} - U_{1}) / 2 + U_{1} + (U_{4} - U_{1}) / 4 & 13 volt \\ E(U_{4} - U_{1}) / 2 + U_{1} + (U_{4} - U_{1}) / 2 & 16 volt \\ D(U_{4} - U_{1}) / 2 + U_{1} + (U_{4} - U_{1}) / 4 - U_{3} & 1 volt \\ F(U_{4} - U_{1}) / 4 - U_{3} + U_{2} & 11 volt \end{matrix}

A kondenzátorok feszültsége, töltése és energiája:

\begin{matrix} C_{1} & (11 - 10)volt=1 volt & 1 \cdot 10^{- 6}coulomb & 0, 5 \cdot 10^{- 6}joule \\ C_{2} & (16 - 11)volt=5 volt & 5 \cdot 10^{- 6}coulomb & 12, 5 \cdot 10^{- 6}joule \\ C_{3} & (6 - 1)volt=5 volt & 5 \cdot 10^{- 6}coulomb & 12, 5 \cdot 10^{- 6}joule \\ C_{4} & (1 - 0)volt=1 volt & 1 \cdot 10^{- 6}coulomb & 0, 5 \cdot 10^{- 6}joule \end{matrix}

A kondenzátorok összes energiája

26 \cdot 10^{- 6}

joule.
Ha

H

és

B

pontokat összekötjük, akkor két külön áramkör alakul ki. Ezek csak egyetlen

H B

pontban függenek össze. Az alsó áramkörben

U_{4} / 2 R

erősségű áram folyik és

A

-hoz képest

E

feszültsége

U_{4} = 16

volt,

H B

feszültsége

U_{4} / 2 = 8

volt. Az

F

pont feszültsége

U_{4} / 2 + U_{2} = 16

volt. Így

C_{2}

kondenzátor mindegyik lemezén egyformán

16

volt a feszültség, tehát ennek a kondenzátornak nincs töltése. qsmallskip

Szabó Zoltán

4. Egy függőleges síktükör előtt elhelyezünk egy vékonyfalú, gömb alakú, vízzel telt akváriumot. Az akvárium sugara

R

és középpontja

3 R

távolságra van a tükörtől. Egy távoli megfigyelő az akvárium középpontján át a tükörre merőlegesen néz. Az akváriumnak a tükörhöz legközelebb levő pontjában egy kis hal úszik

v

sebességgel az akvárium fala mentén. Milyen sebességgel mozognak egymáshoz képest a halnak a megfigyelő által látott képei ? A víz törésmutatója

n = 4 / 3

Megoldás. A hal

1

másodperc alatt

v

utat tesz meg. Ez a szakasz legyen az a tárgy, amelynek kétféle módon keletkezett képét keressük. Csak a tengelyhez közeli sugarakkal, kis szöggel számolunk, ezért mindenütt (töréstörvényben és sinustételben) a szöget használjuk sinusa helyett.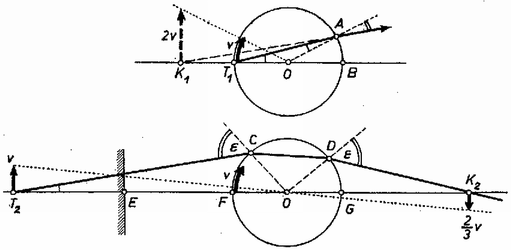

5. ábra

T_{1}

pontban úszó halról mint tárgyról, egyetlen törőfelület ad képet (5. ábra felső rajza). A

T_{1}

-ből

γ = A T_{1} O ∢

alatt induló fénysugár törőszöge

A

-nál a vízben

γ

, a levegőben

n γ

(kettős ívű szög). Ennek a kilépő sugárnak a visszafelé rajzolt meghosszabbítása adja

K_{1}

-ben a virtuális kép helyét. Továbbá

K_{1} A T_{1} ∢ = n γ - γ = (n - 1) γ

. A

K_{1} T_{1} A

háromszögre felírjuk a sinustételt:

\begin{matrix} \frac{K_{1} T_{1}}{K_{1} A} = \frac{(n - 1) γ}{γ} = n - 1. \end{matrix}

Mivel megengedett közelítéssel

K_{1} A = K_{1} O + R

K_{1} T_{1} = K_{1} O - R

, ezért

\begin{matrix} \frac{K_{1} O - R}{K_{1} O + R} = n - 1. \end{matrix}

Innen a virtuális kép távolsága a középponttól:

\begin{matrix} K_{1} O = \frac{n}{2 - n} \cdot R . \end{matrix}

Víznél

n = 4 / 3

és

K_{1} O = 2 R

. Ha a törésmutató nagyobb, mint

2

, a kép reális. A nagyítást a kép- és tárgytávolság hányadosa adja:

\begin{matrix} \frac{K_{1} O}{T_{1} O} = \frac{n}{2 - n} . \end{matrix}

Víz esetében a nagyítás

2

-szeres.
A síktükör

E

-ben van (5. ábra alsó része). Ez a síktükör a tőle

2 R

távolságban levő tárgyról, a

v

sebességnek megfelelő szakaszról a tükör mögött

2 R

távolságban,

T_{2}

ben ad ugyanakkora virtuális képet.

T_{2}

a gömb középpontjától

5 R

távolságban van. Legyen általában

T_{2} O = k R

. A

T_{2}

-ben levő virtuális kép úgy viselkedik, mint egy normális tárgy, amelyet a gömbön mint lencsén át nézünk; a tükörrel ezután már nem kell törődnünk.

T_{2}

reális képét számíthatjuk a vastag lencsék törvényével, de egyenes úton is megkapjuk.
A

T_{2}

-ből

γ = C T_{2} F ∢

szög alatt induló fénysugár

C

-nél levő

ε

beesési szögét keressük. Sinustétellel a

T_{2} O C

háromszögből:

\begin{matrix} \frac{ε}{γ} = \frac{T_{2} O}{C O} = \frac{k R}{R} = k, ε = k γ . \end{matrix}

A törőszög az üvegben:

\begin{matrix} \frac{ε}{n} = \frac{k γ}{n} = D C O ∢ = C D O ∢ . \end{matrix}

Ki kell számítanunk a

D O G ∢

-et. Először

C O F ∢ = ε - γ = k γ - γ = γ (k - 1)

. A

C O D ∢

ugyanúgy

180^{\circ}

-ra egészíti ki a

C

-nél és

D

-nél levő szögek összegét, mint a

C O F ∢

és

D O G ∢

összegét, ezért

\begin{matrix} D O G ∢ + γ (k - 1) = 2 \cdot \frac{k γ}{n} . \end{matrix}

Innen

D O G ∢ = γ (\frac{2 k}{n} - k + 1)

. Felírjuk a

D O K_{2}

háromszögre a sinustételt:

\begin{matrix} \frac{O K_{2}}{D K_{2}} = \frac{ε}{γ (\frac{2 k}{n} - k + 1)} = \frac{k γ}{γ (\frac{2 k}{n} - k + 1)}, \frac{O K_{2}}{O K_{2} - R} = \frac{k}{\frac{2 k}{n} - k + 1} \end{matrix}

Ebből megkapjuk a képtávolságot:

\begin{matrix} O K_{2} = \frac{k n}{n (2 k - 1) - 2 k} \cdot R . \end{matrix}

k = 5

és

n = 4 / 3

, akkor

O K_{2} = 10 R / 3

. A nagyítás:

\begin{matrix} \frac{O K_{2}}{O T_{2}} = \frac{n}{n (2 k - 1) - 2 k} . \end{matrix}

k = 5

és

n = 4 / 3

, akkor a nagyítás

2 / 3

.
Foglaljuk össze a számítások eredményét. A hal valójában

v

sebességgel halad felfelé. Virtuális képe

2 v

sebességgel felfelé, reális képe

2 v / 3

sebességgel lefelé mozog. A két kép relatív sebessége

2 v + 2 v / 3 = 8 v / 3

, az eredetinek

8 / 3

-szorosa.
De most jön a legfontosabb. Mi az egész számítás értelme ? Eddig csak azt tudjuk, hogy a rajzlapon a gömbtől balra egy virtuális kép

+ 2 v

, a gömbtől jobbra

- 2 v / 3

sebességgel mozog. Mindkét mozgás a rajzlapon, a rajzolt képekkel megy végbe, különböző helyeken. De mit lát az ember, ha elvégzi a kísérletet ?
Ha a hal mellett milliméterskála van és ezek képein figyeljük a halképek mozgását, ugyanazokat a mérőszámokat kapjuk, mint a valóságos sebességnél. A sebességek ellentétesek és az egyik sebesség a másiknak háromszorosa lesz, továbbá az egyik hal háromszor olyan hosszú, mint a másik. De most nemcsak erről van szó. Nagyon messziről kell néznünk, hiszen egy messze a gömb mögött levő és egy, a gömb előtt levő képet egyszerre kell élesen látnunk. A két kép távolsága

8, 33 R

. A reális képet is látni lehet szemmel, ha a tiszta látás távolságánál messzebbről nézzük. Itt van annak a jelentősége, hogy a feladat szövege szerint a berendezést messziről kell néznünk. Ekkor a különböző távolságokban levő képekhez vezető egyenesek szögelfordulásait figyeljük meg, és ha elég messziről nézünk, akkor a különböző távolságok ellenére is közelítően

8 / 3

arányban növekedett sebességet észlelünk. Természetesen valahogy informálódnunk kell a hal valóságos

v

sebességéről is.
A sebességnövekedés aránya általános esetben:

\begin{matrix} \frac{2 n}{2 - n} \cdot \frac{(k - 1) (n - 1)}{2 k (n - 1) - n} . \end{matrix}

Érdemes a jelenséget tényleg megfigyelni. Széles, vízzel telt hengerpoharat tükör elé állítunk. A halat függőlegesen a vízbe tartott hurkapálca helyettesíti. A pálca mozgatásakor jól megfigyelhetjük a képek különböző sebességű mozgását.

Tichy-Rács Ádám

Kísérleti feladat. Megmérendő egy adott feszültségforrás

P

hasznos teljesítménye, mint

I

áramerősség függvénye ! Ennek alapján határozzuk meg az elem

R_{b}

belső ellenállását és

U_{0}

elektromotoros erejét ! Rajzoljuk fel a hasznos és összes teljesítmény, valamint

η

hatásfok függését

R

külső ellenállástól !

Az összes teljesítmény

P_{δ} = U_{0} I

, a belső ellenállás teljesítményfogyasztása

I^{2} R_{b}

, tehát a hasznos teljesítmény, mint az áramerősség függvénye:

\begin{matrix} P = U_{0} I - I^{2} R_{b} . \end{matrix}

A grafikon, megegyezésben a képlettel, parabolát ad.

P

hasznos teljesítményt a lemért

U

kapocsfeszültség és

I

áramerősség szorzataként kapjuk meg. Két

P

U

I

értékcsoportból

U_{0}

és

R_{b}

számítható. Nem biztos, hogy a kísérletsorozat folyamán

U_{0}

és

R_{b}

állandó marad.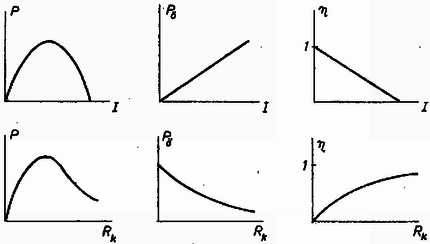

6. ábra

Az összes teljesítmény:

\begin{matrix} P_{δ} = U_{0} I = \frac{U_{0}^{2}}{R_{b} + R_{k}} . \end{matrix}

A hasznos teljesítmény:

\begin{matrix} P = U I = \frac{U_{0}^{2} R_{k}}{{(R_{b} + R_{k})}^{2}} . \end{matrix}

A hatásfok

\begin{matrix} η = \frac{P}{P_{δ}} = \frac{R_{k}}{R_{k} + R_{b}} . \end{matrix}

P_{δ}

és

η

R_{k}

-tól hiperbola-függvény,

P

a fenti törtfüggvény szerint függ. A grafikonokat a 6. ábra mutatja.

Gács Lajos