|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az I. forduló feladatai
1. A padló fölött magasan levő vízszintes lemezen tömegű test van (. ábra). A hozzá kötött hosszú fonál másik végén, közvetlenül a lemez szélénél tömegű test lóg. A súrlódás elhanyagolható. A testeket elengedjük. Egymástól milyen távolságban érik el a testek a padlót? 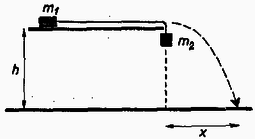 1. ábra
Megoldás. Először egyenletesen gyorsuló mozgás jön létre gyorsulással. Az tömeg földre érésének ideje: Ezalatt az tömeg által elért végsebesség: Ezután számára vízszintes hajítás következik, ennek ideje magasságból , ezalatt a sebességgel megtett út: | |
Ez az eredmény -től független. A mi számadatainkkal . Megvizsgálható, hogy miközben az tömegviszony 0-tól -ig változik, az -tól 0-ig változik.
2. tömegű test vízszintes, súrlódásmentes síkon fekszik két gumifonál között (. ábra). A gumiszálak nyúlása arányos a húzóerővel, a baloldalit erő, a jobboldalit erő képes -rel megnyújtani. Kezdetben a fonalak eredeti hosszúságúak. A testet -rel balra húzzuk, azután elengedjük. Ismertessük a mozgás lefolyását! Rajzoljuk meg az úttörvény grafikonját! . 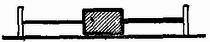 2. ábra
Megoldás. Először a jobboldali, az erősebb fonál hoz létre egy negyed rezgést, amelyre nézve . Ide newton erőt, m-t és 20 kg-ot helyettesítve a szögsebesség és rezgésidő .
A középhelyzetbe a tömeg sebességgel érkezik.
Ezután a baloldali, a gyengébb gumifonál hoz létre egy fél rezgést, amelyre nézve . Ennek a második rezgésnek a szögsebessége és rezgésideje , . Ennek a rezgésnek az indulási sebessége az előbbivel egyező: , innen a második rezgés amplitudója .
A kiszámított adatokkal megrajzolható az úttörvény grafikonja (3. ábra). 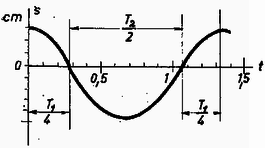 3. ábra
A teljes rezgésidő .
3. átmérőjű, formáját tartó léggömb alul csövön érintkezik a külső levegővel (. ábra a rajza). A léggömb hidrogéntöltéssel indul. Mennyi a léggömb emelő ereje a) a tenger szintjén, b) magasra emelkedve, ahol a légnyomás atmoszféra, c) magasra emelkedve, ahol a légnyomás ? Ha a léggömb ebből a magasságból ismét az előbbi magasságokba kerülne, mennyi volna ott az emelő erő? A burkolat minden -e súlyú. A tenger szintjén a levegő fajsúlya , a hidrogén fajsúlya . A hőmérséklet változatlan. 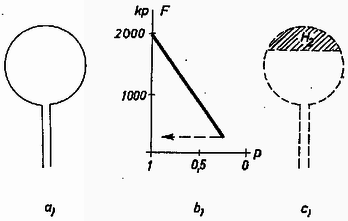 4. ábra
Megoldás. A gömb térfogata , a burkolat súlya . Felfelé menet a gömbben levő hidrogén súlya és a kiszorított levegő súlya a nyomással arányosan csökken, tehát az emelő erő . Az adatok áttekintése: | |
Az emelőerő függését a nyomástól a 4. ábra b) rajza mutatja.
Ha a léggömb lefelé megy, akkor az emelő erő ugyanannyi marad, amennyi a legmagasabb helyzetében volt (szaggatott vonal). Ugyanis az összehúzódó térfogat helyébe ekkor levegő tódul be. Tekintsük most léggömbnek a burkolatot és az elkülönítve képzelt hidrogént (c) rajz). Érthető, hogy a hidrogén súlya és a kiszorított levegő súlya változatlan marad.
A II. forduló feladatai
1. Belül üres, r1=1méter sugarú, m1=670gramm tömegű abroncs φ=53∘08'-es hajlásszögű lejtőn gurul le. Belsejében r2=0,3méter sugarú, m2 tömegű tömör henger a mozgás folyamán az abroncshoz viszonyítva ugyanazt a helyzetét tartja meg úgy, hogy a két tengelyt (az 5. ábrán O és C középpontokat) összekötő egyenes a függőlegessel ψ=36∘52'-es szöget zár be. Mindenütt csúszás nélküli gördülés van. Mekkora a tömör henger tömege? 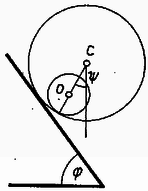 5. ábra
Megoldás. Mindkét tárgy középpontja ugyanazzal az a lejtővel párhuzamos gyorsulással mozog. Ezért és a sima legördülés folytán a szögsebességek:
A szöggyorsulások (v a középpontok lejtővel párhuzamos pillanatnyi sebessége.)
A tehetetlenségi nyomatékok: A hengerre ható forgatónyomaték a forgó mozgás törvénye szerint: | Φ2=β2Θ2=ar2⋅m2r222=am2r22. | (0) |
A középpontok egyenlő a gyorsulására például az energiatételből kaphatunk egy összefüggést. s magasságból leérve a nehézségi erő munkavégzése (m1+m2)g⋅s⋅sinφ. Az eközben megszerzett mozgási energia:
m1v22+m2v22+Θ1ω122+Θ2ω222==v22⋅[m1+m2+m1r12r12+m2r222r22]=v22⋅(2m1+1,5m2)=as(2m1+1,5m2),
mert egyenletesen gyorsuló mozgásnál v2=2as. Egyenlővé tesszük a nehézségi erő munkavégzését a megszerzett mozgási energiával: | (m1+m2)g⋅ssinφ=as(2m1+1,5m2). |
Innen a gyorsulás: | a=g⋅(m1+m2)sinφ2m1+1,5m2. | (I.) |
A rádiuszok nem szerepelnek, de ψ szögről sincs még szó. A henger viselkedésével foglalkozva a gyorsulásra egy másik összefüggést is levezetünk (6. ábra). 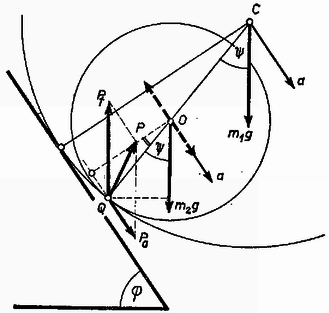 6. ábra
A hengerre két erő hat: m2g súlya és az abroncs részéről P erő Q pontban. E két erő eredőjének O-ban a lejtővel párhuzamos gyorsulást kell okoznia, és forgatónyomaték-eredőjüknek a (0) szerinti Φ2-nek kell lennie. A Q-ban támadó P erőt felbontjuk a lejtővel párhuzamos Pa és a függőleges Pf összetevőkre. Pf-nek m2g-vet kell egyenlőnek lennie (különben az eredő nem eshetne a-ba). O-ban felveszünk ±Pa erőket. A lefelé mutató Pa az m2a gyorsító erő, a felfelé mutató és eredeti Pa, valamint a függőleges erők adják a (0) szerinti Φ2 forgatónyomatékot: | am2r22=m2gr2sinψ-m2ar2cos(φ-ψ). |
Innen a gyorsulás: | a=g⋅sinψ0,5+cos(φ-ψ). | (II.) |
A gyorsulás (I.) és (II.) szerinti eredményeit egyenlővé téve és m2/m1 tömeghányadot kifejezve kapjuk az eredményt: | m2m1=sinψsinφ-3sinψ+2sinφcos(φ-ψ)-1. |
Számadatainkkal φ=53∘08',ψ=36∘52'. sinφ=cosψ=0,8,cosφ=sinψ=0,6. m2/m1=8/67, tehát m2=80 gramm, a=30g/73=0,411g.
2. 20m3-es zárt tartályban 0∘C-on 1atmoszféra nyomáson 26kg levegő van, amelyet 44,2kcal hőmennyiséggel lehet 10∘C-ra melegíteni. A tartályt olyan szeleppel látjuk el, amely csak kifelé enged levegőt, már a legkisebb túlnyomásnál is. Ebben az esetben mekkora hőmennyiség szükséges ahhoz, hogy a tartályban a művelet végén 10∘C-os levegő legyen? A falakon át történő hőveszteség elhanyagolható.
Megoldás. Melegítés közben levegő hagyja el a tartályt, amely levegőt a továbbiak folyamán már nem kell melegíteni. Keressük a tartályban levő levegő tömegét mint az abszolút hőmérséklet függvényét (7. ábra). 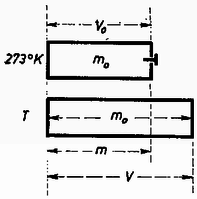 7. ábra
Kezdetben m0 tömeg V0 térfogaton volt 273∘K hőmérsékleten. Állandó nyomáson kiterjedve T Kelvin hőmérsékleten V lenne a térfogat: Ha az eredeti m0 tömeg T fokon V térfogatot tölt be, akkor az eredeti V0 térfogatra m tömeg jut: Tehát a tartályban levő tömeg mint a pillanatnyi hőfok függvénye:
A tartályban levő levegőtömeg dT hőmérséklettel való felmelegítéséhez szükséges hőmennyiség az állandó nyomás melletti fajhő felhasználásával: | dQ=cpmdT=cp⋅273⋅m0⋅1T⋅dT. |
Az egész felmelegítéshez szükséges hőmennyiség: | Q=273⋅m0⋅cp⋅∫273283dTT=273m0cpln283273. |
Feladatunkban cv=44,226⋅10=0,17kcal/kg⋅fok, x=1,4, cp=0,238kcal/kg⋅fok. Az eredmény Q=61,40kcal. Ha a tartály zárt volna és az egész levegőmennyiséget kellene felmelegíteni, ehhez csak 44,2kcal volna szükséges.
3. 2R=4cm átmérője, 40cm gyújtótávolságú gyűjtőlencse tengelyében egy 20cm hosszú, világító fénycső fekszik; közelebbi vége 60cm-re, távolabbi vége 80cm-re van a lencsétől. A lencse túlsó oldalán, a tengelyre merőlegesen felfogó ernyőt helyezünk el. Hová helyezzük ezt az ernyőt, hogy a fényfolt átmérője a lehető legkisebb legyen, és mekkora ez az átmérő?
Megoldás. A tengelyben fekvő fénycső képpontjai szintén a lencse tengelyében feküsznek (8. ábra). 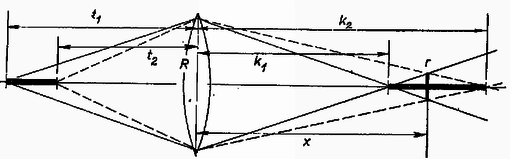 8. ábra
A legszűkebb fénykeresztmetszet a lencsétől x távolságban jön létre, átmérője 2r. A fénycső t1 és t2 távolságban levő végeinek képtávolságai: Hasonló háromszögekből: Ennek az egyenletrendszernek a megoldása x-re, r-re: | x=2k1k2k1+k2,r=R⋅k2-k1k2+k1. |
Felhasználva a képtávolságok előbb kiszámított értékeit: | x=2t1t2f2t1t2-(t1+t2)f,r=R⋅(t1-t2)f2t1t2-(t1+t2)f. |
A fényeső képének hossza k=k2-k1=tf2(t1-f)(t2-f).
A mi számadatainkkal x=96cm, r=0,4cm, k=40cm.
Az 1971. évi fizika tanulmányi verseny eredménye
I. díj Bajmóczy Ervin (Budapest, Fazekas M. Gimn. IV. o. t., Tanára: Hubay Ferenc).
II. díj Mosó Tamás (Budapest, Eötvös J. Gimn., IV. o. t. Tanára: Zentai Károly).
III. díj Szabó Zoltán (Budapest, Apáczai Csere J. Gimn. III. o. t. Tanára: Turtóczky Sándor).
A további helyezettek: 4. Boros Endre (Budapest, I. István Gimn., III. o. t., Tanára: Moór Ágnes); 5. Iglói Ferenc (Szeged, Radnóti M. Gimn., IV. o. t., Tanára: Simon Sándor); 6. Véner Péter (Budapest, Kaffka M. Gimn., IV. o. t., Tanára: Jánosi Ilona); 7. Lázár András (Budapest, Móricz Zs. Gimn., IV. o. t., Tanára: Fehér László); 8. Kövér András (Debrecen, Kossuth L. Gimn., III o. t., Tanára: Czirják Lászlóné); 9. Postásy Csaba (Budapest, Petőfi S. Gimn., IV. o. t.; Tanára: Szondi Lajos); 10. Hámori Iván (Budapest, Radnóti M. Gimn., IV. o. t.).
|
|
 PDF | MathML
PDF | MathML 






