Kezdőlap


Cím:	Sztatikai feladatok megoldása I.
Szerző(k):	Mihály László
Füzet:	1971/szeptember, 34 - 38. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hidak, épületek tervezése gyakran vet fel olyan problémákat, amelyekben egy szerkezetre ható erők nagyságát és irányát kell meghatározni. A megoldáshoz felhasználjuk, hogy a vizsgált tárgy nem mozog, egyensúlyban van. Az ilyen jellegű feladatok megoldásával a fizika egy külön ága: a sztatika foglalkozik. A tanulmányaink során megismert feladatok megoldása nemcsak azért fontos, mert az egyszerűbbtől a bonyolultabb felé haladva eljuthatunk a fenti problémákhoz, hanem azért is, mert a gyakorló példák megoldásával olyan gondolkodásmódot sajátíthatunk el, amely a mechanika más ágainak tanulásához is alapot ad.
A legbonyolultabb sztatikai feladat is megoldható (kivételt képeznek a sztatikailag határozatlan szerkezetek), és a megoldás a tapasztalattal egyezik, ha igaznak tekintjük az alábbi három törvényt:
1. egy merev test egyensúlyban van, ha a rá ható erők ( $F_{1}$ , $F_{2}$ , $...$ , $F_{n}$ ) összege nulla;
2. ezen erők forgatónyomatékainak ( $M_{1}$ , $M_{2}$ , $...$ , $M_{n}$ ) összege a merev test bármely pontjára vonatkoztatva nulla;
3. ha az $A$ test a $B$ -re valamilyen erővel $(F_{A B})$ hat, akkor a $B$ test az $A$ -ra olyan $(F_{B A})$ erővel hat, amely az előzővel egyező nagyságú, azonos hatásvonalú, és ellentétes irányú.
A feladatok megoldásánál e három törvény alapján állítunk fel egyenletrendszert, melynek megoldása szolgáltatja a keresett erőket. A törvények matematikai alakja:

\begin{matrix} F_{1} + F_{2} + ... + F_{n} = 0, & (1) \\ M_{1} + M_{2} + ... + M_{n} = 0, & (2) \\ F_{A B} = - F_{B A} . & (3) \end{matrix}

Szinte hihetetlennek tűnik, hogy az egyensúlyi feladatok nagy része (a tanulmányainkban előforduló valamennyi feladat) ezzel a három egyszerű egyenlettel megoldható. Elsősorban az okoz nehézséget, hogy az egyenletek mögött rejlő fizikai tartalom megértéséhez, az egyenletek helyes alkalmazásához kellő gyakorlat szükséges. Ennek megszerzéséhez szeretnénk segítséget nyújtani. (Ismertnek tekintjük az alapvető trigonometriai azonosságokat, továbbá támaszkodunk a középiskolában fizikából tanultakra.) Az új gondolatok könnyebben érthetők, ha alkalmazásukat konkrét példán szemléltetjük, ezért meg fogjuk oldani az alábbi két feladatot.
1. feladat. Felezőpontjukban

G_{1}

és

G_{2}

súllyal terhelt,

l

hosszúságú súlytalan gerendákból az

1

. ábra szerinti tartót készítjük, melynek végére

G

súlyú terhet akasztunk. Mekkora erők hatnak az

A

és

B

pontban a falra és a

C

pontban a rudakat összekötő tengelyre?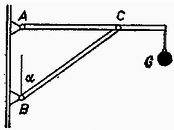

1. ábra

2. feladat. Legfeljebb mekkora súllyal terhelhető a

8

. ábra szerinti kötél elrendezés, ha az

A

kötélág maximálisan

S_{A}

, a

B

kötélág maximálisan

S_{B}

erőt bír el?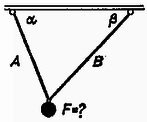

8. ábra

A feladat megoldását mindig azzal kezdjük, hogy részletes rajzot készítünk a vizsgált szerkezetről, amelyen feltüntetjük a szerkezetre ható ismert és ismeretlen erőket (

2

. ábr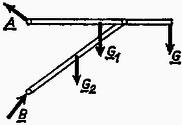a).

2. ábra

Összetettebb problémánál a szerkezetet részekre bontjuk, és mindegyik részt önálló egységnek tekintve, az egyensúly feltételét külön-külön vizsgáljuk. Így elérhető, hogy a sok ismeretlen erő meghatározásához kellő számú egyenlet álljon rendelkezésünkre (

3

. ábr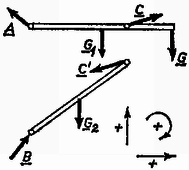a).

3. ábra

A részekre bontás teljesen önkényesen történhet; a feladatban szereplő alkatrészeket képzeletben akárhol elfűrészelhetjük, és az elhagyott részt az általa kifejtett erővel helyettesíthetjük (

4

. ábr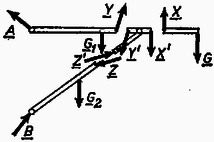a).

4. ábra

A megoldásnak ez az első lépése kulcsfontosságú; ha jól ,,darabolunk'', a megoldás a továbbiakban nagyon egyszerűvé válik.
Az erők irányának berajzolásánál törekedjünk arra, hogy az körülbelül egyezzen a valódi iránnyal. Ha a valódi irányt nem tudjuk előre megjósolni, akkor tetszőlegesen rajzoljuk be az erőt; az egyenletrendszer megoldása után mindenképpen meg tudjuk mondani a helyes irányt. (Ha például egy erőre negatív számot kapunk, akkor ez azt jelenti, hogy a valóságban a rajzolttal ellentétes irányú.) Mindenképpen szem előtt kell tartani a következőket:
‐ Kötélben mindig kötélirányú húzóerő ébred. (Ez annak a következménye, hogy a kötél ‐ szemben a merev rúddal ‐ forgatónyomatékot nem tud továbbítani. Aki akarja, ennek alapján az

(1)

és

(2)

egyenlőséget a kötél egy darabjára felírva bizonyíthatja a tételt.)
‐ Súrlódásmentes felület által kifejtett erő merőleges a felületre.
‐ Mindig teljesülnie kell a

(3)

egyenlőségnek (tehát a

3

. és

4

. ábrán a

C

C'

;

X

X'

;

Y

Y'

;

Z

Z'

erők páronként egyenlő nagyságúak és ellentétes irányúak).
Miután a problémát ily módon részletekre bontottuk, sor kerülhet az

(1)

(2)

egyenletek alkalmazására.
Az

(1)

egyenlet a testre ható erőkre vonatkozik. Az egyenlet szempontjából közömbös a testre ható erők támadáspontjának helye; összegzéskor az erővektorokat önmagukkal párhuzamosan tetszőleges helyre csúsztathatjuk. A fenti alakban azonban az egyenlettel sajnos nem tudunk számolni, mert benne vektormennyiségek szerepelnek.
Az alábbiakban három módszert mutatunk be, amelyekkel az egyenletet a gyakorlatban használható alakra hozhatjuk. Mindhárom módszer azon alapszik, hogy a vektorok összege akkor és csak akkor nulla, ha a belőlük alkotott nyílfolytonos törtvonal zárt; az utolsó vektor végpontja az első kezdőpontjával esik egybe (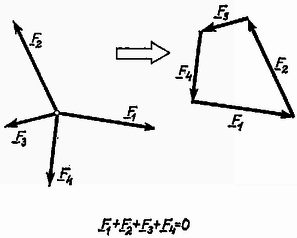

5

. ábra).

5. ábra

a) A

6

. ábrából látható, hogy a vektorokból kapott törtvonal csak akkor zárt, ha a vektorokat két (nem párhuzamos) egyenesre merőlegesen vetítve, és a kapott szakaszok előjeles hosszát algebrailag összegezve, végeredményül mindkét esetben nullát kapunk. Egy egyenes azért nem elég, mert lehetséges, hogy a különbségvektor merőleges rá (a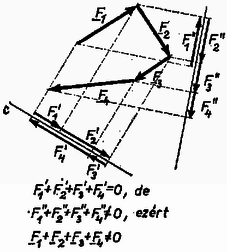

6

. ábrán a

c

egyenes).

6. ábra

b) Abban a speciális esetben, amikor a két egyenes merőleges egymásra, derékszögű koordinátarendszert kapunk, és a vektorok vetületeinek összege maga a felbontott vektor. Azokat a vektorokat, melyek összegül a felbontott vektort adják, a vektor komponenseinek nevezzük. Derékszögű koordinátarendszerben tehát egy vektor komponensei és vetületei egybeesnek. Az

(1)

vektoregyenlet akkor teljesül, ha a vektorok komponenseinek összege külön-külön nulla.
c) A komponensekre bontás ferdeszögű koordinátarendszerben is lehetséges. Itt is igaz, hogy a vektorok összege akkor és csak akkor nulla, ha a komponensek összege külön-külön nulla.
A vektorok jellemzésére általában nagyságukat és irányukat használjuk, de teljesen jellemeztünk egy vektort akkor is, ha meghatározzuk egy adott koordináta-rendszerbeli komponenseit. Bármilyen módszert használunk azonban, egy vektor jellemzésére síkbeli problémánál mindig kettő, térbelinél három adat kell.
A

7

. ábrán láthatjuk, hogy a fenti három esetben a szereplő vektorokat hogyan kell felbontani. A vetületek, ill. komponensek meghatározásánál geometriai tételeket használtunk fel. (Gyakorlásképpen ellenőrizzük a kapott képleteket!)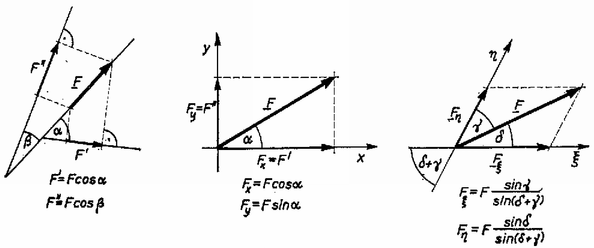

7. ábra

Végeredményben mindhárom esetben az

(1)

vektoregyenletből két skaláregyenletet kapunk. Térbeli problémánál térbeli koordinátarendszert kell használni; ebben az (általános) esetben tehát az

(1)

vektoregyenlet három skaláregyenlettel egyenértékű.
Az eddigiek gyakorlására oldjuk meg a

2

. feladatot! Képzeletben vágjuk el az összekötési pont közelében mindhárom kötelet. A vágási felületen a kivágott darabra a kötél irányába mutató erők hatnak (

9

. ábr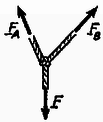a).

9. ábra

Az egyensúly feltétele:

\begin{matrix} F_{A} + F_{B} + F = 0. \end{matrix}

Ismeretlennek tekintjük az

F_{A}

és

F_{B}

erőket. A két ismeretlen megtalálásához két egyenletre van szükség. Ezen egyenleteket az egyensúly feltételéből a fent tárgyalt három módszer valamelyikével kapjuk.
a) Kézenfekvő az erőket a kötelek egyenesére vetíteni. Azt, hogy melyik kötélre vetítünk, a felső index jelöli (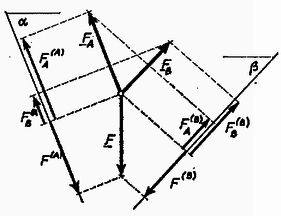

10

. ábra).

10. ábra

\begin{matrix} F_{A}^{(A)} & = F_{A}, F_{A}^{(B)} = F_{A} cos [180^{\circ} - (α + β)], \\ F_{B}^{(A)} & = F_{B} cos [180^{\circ} - (α + β)], F_{B}^{(B)} = F_{B}, \\ F^{(A)} & = - F sin α, F^{(B)} = - F sin β . \end{matrix}

A két egyenlet:

\begin{matrix} F_{A} + F_{B} cos [180^{\circ} - (α + β)] - F sin α = 0 az (A) vetületekre, \\ F_{A} cos [180^{\circ} - (α + β)] + F_{B} - F sin β = 0 a (B) vetületekre . \end{matrix}

Az egyenletrendszer megoldása:

\begin{matrix} F_{A} = F \frac{sin α + sin β cos (α + β)}{sin^{2} (α + β)} = F \frac{cos α}{sin (α + β)}, \\ F_{B} = F \frac{sin β + sin α cos (α + β)}{sin^{2} (α + β)} = F \frac{cos β}{sin (α + β)} . \end{matrix}

b) Válasszunk olyan derékszögű koordinátarendszert, amelynek

y

tengelye függőleges. Ekkor:

\begin{matrix} F_{A x} = - F_{A} cos α, & F_{A y} = F_{A} sin α, \\ F_{B x} = F_{B} cos β, & F_{B y} = F_{B} sin β, \\ F_{x} = 0, & F_{y} = - F . \end{matrix}

Az egyensúly feltétele:

\begin{matrix} - F_{A} cos α + F_{B} cos β = 0 az x \end{matrix}