Kezdőlap


Cím:	1970. évi Eötvös Loránd Fizikaverseny
Füzet:	1971/február, 81 - 84. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat október $17$ -én rendezte $47$ . versenyét Budapesten és $7$ vidéki városban az idén érettségizettek és a középiskolások részére. A versenyzők $5$ óráig dolgozhattak és bármilyen segédeszközt használhattak. Ismertetjük a verseny feladatait, megoldásaikat és a nyertesek névsorát.

1. Egyenes körhenger fele ezüstből, fele alumíniumból készült, ezért súlypontja az

R = 10 cm

-es rádiusz középponttól mért negyedében van. A henger tengelyét vízszintesen csapágyazzuk és abban a helyzetben, amikor súlypontja a legmélyebben van, a kerületére csavart fonál végére egy tömeget akasztunk, azután a szerkezetet elengedjük. Mennyi a henger szögsebessége egy teljes fordulat után, ha a lelógó

m_{1}

tömeg
a) a henger

m

tömegével egyenlő,
b) a henger tömegének nyolcada?

Megoldás. A henger és a lelógó tömeg helyzetét

α

elfordulási szöggel adjuk meg (1. ábra).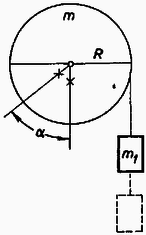

1. ábra

Először keressünk sztatikus egyensúlyi helyzetet, amikor egy bizonyos

α

szög mellett a forgatónyomatékok egyenlők. Ennek feltétele: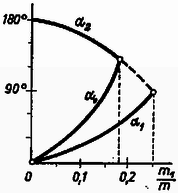

\begin{matrix} m g \cdot \frac{R}{4} \cdot sin α = m_{1} g R . \end{matrix}

Ebből az egyensúlyi helyzet feltétele:

sin α = 4 m_{1} / m

. Ilyen sztatikus egyensúlyi helyzet addig van, amíg

m_{1} / m ≦ 1 / 4

. Az

α_{1}

hegyesszöghöz tartozó egyensúlyi helyzet stabilis, az

α_{2}

tompaszöghöz tartozó labilis. Például

m_{1} / m = 1 / 8

esetében

α_{1} = 30^{\circ}

α_{2} = 150^{\circ}

. Ha

m_{1} / m = 1 / 4

α_{1} = α_{2} = 90^{\circ}

. A sztatikus egyensúlyi helyzetek szögét a 2. ábra alsó és felső görbéje mutatja az

m_{1} / m

tömegviszony függvényében.

2. ábra

Ha szerkezetünket

α = 0^{\circ}

-os helyzetéből elengedjük, akkor

α

szögnyi elfordulás után a lelógó tömeg súlyának munkavégzése

m_{1} g α R

. Ebből került ki a henger súlypontjának emeléséhez szükséges

m g R (1 - cos α) / 4

munkavégzés, a henger

Θ ω^{2} / 2

mozgási energiája és a lelógó tömeg

m_{1} v^{2} / 2 = m_{1} R^{2} ω^{2} / 2

mozgási energiája. Az energiamegmaradás törvénye szerint:

\begin{matrix} m_{1} g α R = \frac{m g R (1 - cos α)}{4} + \frac{Θ ω^{2}}{2} + \frac{m_{1} R^{2} ω^{2}}{2} . \end{matrix}

Hengerünk tehetetlenségi nyomatéka egyszerűen

Θ = m R^{2} / 2

, ezért:

\begin{matrix} m_{1} g α R = \frac{m g R (1 - cos α)}{4} + \frac{m R^{2} ω^{2}}{4} + \frac{m_{1} R^{2} ω^{2}}{2} . \end{matrix}

Innen a henger szögsebessége, mint

α

elfordulási szög függvénye:

\begin{matrix} ω = \sqrt[]{\frac{4 \cdot \frac{m_{1}}{m} \cdot α + cos α - 1}{2 \cdot \frac{m_{1}}{m} + 1} \cdot \frac{g}{R}} \end{matrix}

Az a) kérdésre a felelet: ha

m_{1} / m = 1

, akkor

α = 2 π

mellett

ω = \sqrt[]{8 π g / 3 R} = 28, 65 s^{- 1}

Ha az

m_{1} / m

tömegviszony kisebbedik,

ω

képletében a tört számlálója mindig kisebb lesz és egy bizonyos

α_{0}

szög esetében nulla lesz, ennek feltétele:

\begin{matrix} 4 \cdot \frac{m_{1}}{m} \cdot α_{0} + cos α_{0} - 1 = 0. \end{matrix}

Egyenletünk közelítéssel oldható meg. A 2. ábra középső görbéje tünteti fel a maximális felemelkedés szögének,

α_{0}

-nak az

m_{1} / m

tömegviszonytól való függését.
Vizsgáljuk meg a szerkezet viselkedését különböző

m_{1} / m

tömeghányadoknál, a kisebbektől a nagyobbak felé haladva. Ha

m_{1} / m

elég kicsiny, a henger kezd forogni, a szögsebesség

α_{1}

stabilis egyensúlyi helyzeten áthaladva a legnagyobb, azután lassul és a henger nem éri el

α_{2}

labilis egyensúlyi helyzetet, hanem még előbb visszafordul. Növelve a tömegviszonyt egy bizonyos esetben a henger eléri

α_{2}

felső, labilis egyensúlyi helyzetét, majd ezen át is lendül. A határeset akkor jön létre, ha

α_{0}

egyenlő lesz

α_{2}

-vel. Közelítő számítás mutatja, hogy ez

m_{1} / m = 0, 181

tömegviszonynál következik be. Ekkor

α_{0} = α_{2} = {133, 5}^{\circ}

.
A felelet b) kérdésre: a henger nem fordul át.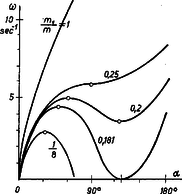

3. ábra

A 3. ábra

ω

szögsebesség

α

szögtől való függését mutatja különböző tömegviszonyok esetében. Amíg

m_{1} / m

értéke

0, 181

és

0, 25

között van, a szögsebességnek minimuma van

α_{2}

helyzetben.

2. A repülőgép állandó sebességű vízszintes repüléséhez szükséges tolóerő

F = k_{1} A v^{2}

. A szárnyfelület által létrehozott emelő erő

Q = k_{2} A v^{2}

. (

Q

a repülőgép súlya,

A

a szárnyfelület nagysága,

v

a sebesség.) A szárnyfelület súlya

k_{3} A

, ehhez járul a teher

Q_{0}

súlya. Mekkora teljesítmény kell a repülőgép mozgásban tartásához? Mikor minimális a teljesítmény? Képes-e az ember izomerejével repülni? Ekkor

k_{1} = 0, 001 kp \cdot m^{- 2} \cdot {(m/s)}^{- 2}

k_{2} = 25 k_{1}

Q_{0} = 100 kp

k_{3} = 2 {kp/m}^{2}

Megoldás. A teljesítmény az erő és a sebesség szorzata, a repülőgép esetében

P = F v = k_{1} A v^{3}

. De itt az

A

szárnyterület és a

v

sebesség nem függetlenek egymástól, mert az emelő erőnek a gép

Q_{0} + k_{3} A

súlyával kell egyenlőnek lennie:

\begin{matrix} Q_{0} + k_{3} A = k_{2} A v^{2} . \end{matrix}

Ebből kifejezhető a szükséges szárnyterület mint a sebesség függvénye:

\begin{matrix} A = \frac{Q_{0} / k_{2}}{v^{2} - k_{3} / k_{2}} . \end{matrix}

Ezt felhasználva a teljesítmény kifejezésében, a teljesítményt mint a sebesség függvényét kapjuk meg:

\begin{matrix} P = \frac{k_{1} Q_{0}}{k_{2}} \cdot \frac{v^{3}}{v^{2} - k_{3} / k_{2}} . \end{matrix}

A sebesség szerint differenciálva keressük a teljesítmény minimumát:

\begin{matrix} \frac{k_{2}}{k_{1} Q_{0}} \cdot \frac{d P}{d v} = \frac{3 v^{2} (v^{2} - k_{3} / k_{2}) - 2 v^{4}}{{(v^{2} - k_{3} / k_{2})}^{2}} . \end{matrix}

A differenciálhányados eltűnése a minimum szükséges feltétele:

\begin{matrix} 3 (v^{2} - k_{3} / k_{2}) - 2 v^{2} = 0. \end{matrix}

Az a sebesség, amely mellett a repülés minimális teljesítményű:

\begin{matrix} v = \sqrt[]{\frac{3 k_{3}}{k_{2}}} . \end{matrix}

Ebben az esetben a szárnyfelület területe:

\begin{matrix} A = \frac{Q_{0} / k_{2}}{3 k_{3} / k_{2} - k_{3} / k_{2}} = \frac{Q_{0}}{2 k_{3}}, \end{matrix}

illetve

Q_{0} = 2 k_{3} A

, vagyis a minimális teljesítmény esetében a szárny súlya a teher súlyának a fele. A minimális teljesítmény:

\begin{matrix} P = \frac{k_{1}}{k_{2}} \cdot \frac{3 Q_{0}}{2} \sqrt[]{\frac{3 k_{3}}{k_{2}}} . \end{matrix}

A mi adatainkkal a szárny területe

25 m^{2}

, az egész repülőgép súlya

150 kp

, a tolóerő

6 kp

, a sebesség

15, 49 m/s = 55, 6 km/óra

, a teljesítmény

92, 9 mkp/s = 910 watt = 1, 24 LE

. Az emberi izomerővel aligha vagyunk képesek repülni. Táblázatunk a teljesítmény minimumának kialakulását mutatja.

\begin{matrix} A & Q & v & F & P \\ m^{2} & kp & m/s & kp & mkp/s \\ 10 & 120 & 21,9 & 4,8 & 104 \\ 15 & 130 & 18,6 & 5,2 & 96,8 \\ 20 & 140 & 16,7 & 5,6 & 93,6 \\ 25 & 150 & 15,49 & 6,0 & 92,9 \\ 30 & 160 & 14,6 & 6,4 & 93,8 \\ 35 & 170 & 13,9 & 6,8 & 94,2 \end{matrix}

0, 5 mm

széles rést

20 cm

-es gyújtótávolságú lencsével a lencsétől

100 cm

-re levő ernyőre képezünk le olyan fénnyel, amely

0, 4 μ

hullámhosszúságú kék és

0, 6 μ

hullámhosszúságú piros fény keveréke. A lencsére

0, 04 mm

rácsállandójú optikai rácsot helyezünk. Mit látunk az ernyőn?

Megoldás. A rés leképezésekor a tárgytávolság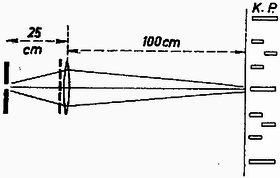

25 cm

, a képtávolság

100 cm

, a lineáris nagyítás

4

-szeres, és a rés képe

2 mm

széles sáv (4. ábra).

4. ábra

Ezt a képet a kék és piros fény keveréke alkotja, tehát bíbor színűnek látjuk. Azok az irányok, amelyekben a rács erősítést ad:

sin α = n λ / d

, ahol

λ

a hullámhossz,

d

a rácsállandó és

n

egész szám. Adatainkkal a kék fény számára

sin α = 0, 01 n

, a piros fény számára

sin α = 0, 015 n

. Tekintettel a

100 cm

-es ernyőtávolságra a kék fény erősítései

10 mm

-es, a piros fény erősítései

15 mm

-es távolságokban következnek egymás után. Minden harmadik kék és minden második piros erősítés ugyanarra a helyre. esik és bíbor színt ad.

A verseny eredménye. I. díjat nyertek Blahó Gábor (a budapesti Eötvös Gimnázium IV. o.-ban Zentai Károly tanítványa) és Harmat Péter (a budapesti ELTE-TTK fizikus hallgatója, tavaly a mosonmagyaróvári Kossuth Gimnáziumban Krajnik József tanítványa volt). II. díjat nyertek Bajmóczy Ervin IV. o. t. (a budapesti Fazekas Gimnáziumban Hutai Ferenc tanítványa) és Tichy-Rács Ádám IV. o. t. (a budapesti Eötvös Gimnáziumban Zentai Károly tanítványa). III. díjat nyert Mosó Tamás IV. o. t. (a budapesti Eötvös Gimnáziumban Zentai Károly tanítványa). Dicséretet kaptak: Füredi Gábor IV. o. t. (a budapesti Móricz Gimnáziumban Fehér László tanítványa), Horváthy Péter (a budapesti ELTE-TTK matematikus hallgatója, tavaly a budapesti Fazekas Gimnáziumban Mihály István tanítványa), Láz József (a budapesti ELTE-TTK fizikus hallgatója, tavaly a budapesti Eötvös Gimnáziumban Kellner Dénes tanítványa) és Sánta Imre IV. o. t. (a szegedi Radnóti Gimnáziumban Simon Sándor tanítványa).