Kezdőlap


Cím:	Pályázat az inverzióról (befejező közlemény)
Szerző(k):	Bártfai Pál , Tusnády Gábor
Füzet:	1971/december, 193 - 201. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az inverzióról szóló pályázatunk¹ ötlete tulajdonképpen az 1968. évi Nemzetközi Matematikai Diákolimpia egyik példájának megoldásakor keletkezett. A példa számolás mentes megoldását kerestük, és a keresés közben találtuk a feladatnak a pályázat kiírásakor tárgyalt általánosítását, majd ennek az inverzió felhasználásával történő bizonyítását. Most, hogy a pályázatra beérkezett dolgozatokat végigolvastuk, végre megtaláltuk az eredeti feladat inverzió-mentes (és természetesen számolás mentes) megoldását. Számunkra a pályázat már csak ezért is sikeresnek mondható, reméljük, hasonlóan sikeresnek érzik pályázatunkat mindazok, akik részt vettek benne. Azoknak pedig, akik nem vettek részt, azt javasoljuk, hogy az alább közölt megoldások elolvasása előtt mindig álljanak meg egy kis időre, és próbálják az egyes feladatokat önállóan megoldani. Lapunk szokásainak megfelelően igyekeztünk a pályázók megoldásai közül kiválasztani a legszebbet, a névaláírások mellől hiányzó osztály- és iskolajelzések a díjak odaítéléséről szóló jelentésben² megtalálhatóak.

1. feladat. Legyen az inverzió alapkörének középpontja

O

, sugara

r

, a sík két tetszőleges,

O

-tól különböző pontja

Q

és

S

, ezek inverze

Q'

és

S'

. Bizonyítandó, hogy

\begin{matrix} \frac{Q' S'}{Q S} = \frac{O S'}{O Q} = \frac{O Q'}{O S} . \end{matrix}

Megoldás. Az inverzió definíciója szerint

Q'

és

S'

O Q

, illetve

O S

félegyenesnek az a pontja, melyre

\begin{matrix} O Q' \cdot O Q = O S' \cdot O S = r^{2}, \end{matrix}

amiből állításunk

\frac{O S'}{O Q} = \frac{O Q'}{O S}

része közvetlenül adódik. Mérjük fel az

O Q

félegyenesre az

O S'

szakaszt, az

O S

félegyenesre pedig az

O Q'

szakaszt, és jelöljük a kapott végpontokat

Q_{1}

gyel, illetve

S_{1}

gyel (1. ábra).

1. ábra

Mivel

O Q : O Q_{1} = O Q : O S' = O S : O Q' = O S : O S_{1}

, és

Q_{1}

S_{1}

O Q

, illetve

O S

félegyeneseken vannak,

O

az az centrumú hasonlóság, mely

Q

-t

Q_{1}

be viszi, az

S

pontot

S_{1}

be viszi, és így

Q S : Q_{1} S_{1} = O Q : O Q_{1}

.
Legyen

t

az az egyenes, amelyre tükrözve az

O Q

félegyenes az

O S

félegyenesbe megy át (ezt az egyenest a

Q O S

szög felezőjének nevezzük; ha a

Q

O

S

pontok egy egyenesen vannak, akkor

t

merőleges erre az egyenesre és átmegy

O

-n, vagy azonos ezzel az egyenessel aszerint, hogy

O

elválasztja-e a

Q

S

pontokat vagy sem). A

t

-re való tükrözés a

Q_{1}

pontot

S'

-be,

Q'

-t

S_{1}

-be viszi át, tehát

Q_{1} S_{1} = Q' S'

, és így

Q' S' : Q S = Q_{1} S_{1} : Q S = O Q_{1} : O Q = O S' : O Q

, amint azt bizonyítanunk kellett.

Lakatos Béla

2. feladat. Adott a síkban három különböző pont:

A

B

C

. Szerkesszük meg azt a kört, mely átmegy

C

-n és amelyikre

A

-t invertálva

B

-t kapjuk.

1. megoldás. Legyen a keresett

k

kör középpontja

O

(2. ábr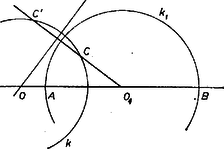a).

2. ábra

Mivel

O A \cdot O B = O C^{2}

, az

A B

szakasz fölé rajzolt,

k_{1}

-gyel jelölt Thalész-körhöz

O

-ból húzott érintő hossza

O C

. Másképpen fogalmazva, a

k

és

k_{1}

körök merőlegesen metszik egymást. Ebből következik, hogy

k

-nak

k_{1}

-re vonatkozó inverze önmaga, ezért

k

átmegy

C

-nek

k_{1}

-re vonatkozó inverzén,

C'

-n is (ha

C' \equiv C

, akkor ráadásul

O C

érinti

k

-t).

C'

birtokában egyértelműen megszerkeszthető a feladatnak eleget tevő

k

kör. Egyetlen kivétel, ha

C O_{1} ⊥ A B

(ahol

Q_{1}

k_{1}

középpontja), azaz ha

C A = C B

, mert ekkor

C C'

felező merőlegese nem metszi

A B

-t, ekkor a feladatnak nincs megoldása.

Pap Gyula

2. megoldás. Szerkesszük meg először

A

és

B

inverzét a

C

középpontú, tetszőleges

k_{2}

körre vonatkozólag (3. ábra), jelöljük ezeket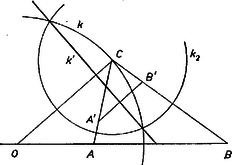

A'

és

B'

-vel.

3. ábra

A keresett

k

kör

k'

inverze

k_{2}

is vonatkozólag egyenes lesz, melyre nézve

A'

és

B'

tükrös párt alkotnak (pontversenyen kívüli 31. probléma¹).

k'

tehát az

A' B'

felező merőlegese, ezt visszainvertálva kapjuk

k

-t.

k

egyenes lesz, ha

k'

átmegy

C

-n, azaz ha

C A' = C B'

, de ekkor

C A = C B

. Tehát ha

C A = C B

, akkor a feladatnak nincs megoldása.

k'

inverzének szerkesztése két esetre bomlik. Ha

A

B

és

C

háromszöget alkot, akkor a 3. ábrából könnyen leolvasható, hogy a

C

-n keresztülmenő, az

A' B'

-vel párhuzamos egyenes kimetszi

A B

-ből a keresett kör középpontját. Ha

A

B

és

C

egy egyenesbe esik, akkor az inverzió alapkörét célszerű úgy felvenni, hogy ne tartalmazza sem

A

-t, sem

B

-t.

A'

és

B'

ekkor

k

belsejébe kerülnek,

k'

két pontban metszi

k_{2}

-t, s ezek

C

-vel együtt a keresett kör három pontját adják.

Megjegyzés. Ha

A

B

és

C

háromszöget alkotnak, akkor a feladatra több szép egyszerű megoldás van. Ezek közül kettőt bizonyítás nélkül említünk:
1. Az

A B C

háromszög körülírt körének

C

-beli érintője kimetszi

A B

-ből a keresett kör középpontját.
2. A

C

szög külső és belső szögfelezőinek

A B

-vel alkotott metszéspontjai a keresett kör átmérőjének végpontjai.

3. feladat. Adott a síkban három különböző pont:

A

B

és

C

. Legyen

k_{a}

A

-n átmenő,

B

-t

C

-be vivő,

k_{b}

B

-n átmenő,

C

-t

A

-ba vivő,

k_{c}

, a

C

-n átmenő,

A

-t

B

-be vivő inverzió alapköre. Mutassuk meg, hogy van két pont, amelyeken e három kör mindegyike átmegy.

1. megoldás. Mindenekelőtt fel kell tételeznünk, hogy az

A B

A C

B C

szakaszok különböző hosszúak, mert ellenkező esetben a szóban forgó körök valamelyike nem létezik.
A

k_{c}

, kör elválasztja

A

-t és

B

-t, legyen pl.

A

k_{c}

belsejében (4. ábra).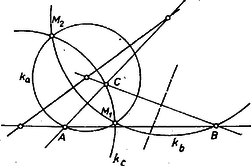

4. ábra

Ekkor

A C

minden pontja, a

C

kivételével,

k_{c}

belsejébe esik. A

k_{b}

kör áthalad

B

-n és

A C

-t egy belső pontba metszi, tehát

k_{b}

-nek a

k_{c}

-n kívüli pontja

B

, és van

k_{c}

-n belüli pontja is, ilyen például az

A C

szakaszon levő pontja, azaz

k_{b}

és

k_{c}

két pontban metszik egymást: legyenek ezek

M_{1}

és

M_{2}

.
Invertáljuk

k_{b}

-t

k_{c}

-re, a kapott

k_{b}'

átmegy

A

-n, és mivel

A

és

C

inverz pár

k_{b}

- re, azért

B

és

C

is inverz pár lesz

k_{b}'

-re (lásd 31. probléma). Mivel a 2. feladat megoldása egyértelmű, ebből következik, hogy

k_{b}'

azonos

k_{a}

-val. Így, ha

k_{b}

M_{1}

és

M_{2}

-ben metszette

k_{c}

-t, ugyanott metszi

k_{b}

-t

k_{b}

-nek

k_{c}

-ra vonatkozó inverze,

k_{a}

is, s ezt akartuk bizonyítani.

Juhász György, Tóth András

2. megoldás. Tegyük fel, hogy

A B > B C > A C

. Az I. példa alapján (Apollóniosz-kör), felhasználva a 2. feladatban bizonyított egyértelműséget,

k_{a}

B

és

C

pontokhoz és a

λ = \frac{A B}{A C}

arányhoz tartozó Apollóniosz-kör. Az Apollóniosz-kör sohasem metszheti a szakaszfelező merőlegest, mindig az általa meghatározott két félsík valamelyikén van, jelenleg azon, amelyikre

A

esik. Mivel a

B

és

C

pontok

k_{a}

-ra inverz pontok, egyikük a kör belsejében van, de akkor ez csak

C

lehet, míg

B

kívül van. Hasonlóan igazolható, hogy

k_{b}

is tartalmazza

C

-t, míg

A

kívülre esik. A

k_{a}

és

k_{b}

köröknek van közös belső pontjuk,

C

, de egyik sem tartalmazhatja a másikat, ezt mutatja a

B

és

A

pont helyzete, tehát

k_{a}

és

k_{b}

két pontban (

M_{1}

és

M_{2}

) metszik egymást. Az Apollóniosz-kör definíciója szerint

M_{1} B : M_{1} C = A B : A C

és

M_{1} C : M_{1} A = B C : B A

. A két egyenlőséget összeszorozva

M_{1} B : M_{1} A = B C : A C

, ami azt mutatja, hogy a harmadik Apollóniosz-kör,

k_{c}

is átmegy

M_{1}

-en. Ugyanezt mondhatjuk el

M_{2}

-ről is.

Boros Endre, Petz Dénes

4. feladat. Adott a síkban három különböző pont:

A

B

C

. Jellemezzük azokat a köröket, melyekre invertálva az adott pontokat, a kapott

A'

B'

C'

pontokra

A' C' = B' C'

teljesül.

1. megoldás. Az 1. feladat eredményét felhasználva tetszőleges

O

középpont esetén:

\begin{matrix} C A : C' A' = O A : O C', & (1) \\ C B : C' B' = O B : O C' . \end{matrix}

\begin{matrix} A' C' = B' C', \end{matrix}

(2)

akkor a két egyenletet elosztva kapjuk, hogy

\begin{matrix} \frac{C A}{C B} = \frac{O A}{O B} . \end{matrix}

(3)

Megfordítva, ha (3) teljesül, (1)-gyel összevetve adódik (2).

O

tehát akkor és csak akkor tartozik a mértani helyhez, ha (3) teljesül és

C'

létezik. Az

O

pontok mértani helye az I. példa alapján felírt, az

A

és

B

pontokhoz tartozó Apollóniosz-kör, kizárva belőle a

C

pontot. Az inverzió alapkörének sugara tetszőleges lehet. Ha

C A = C B

, akkor a mértani hely az

A B

oldalfelező merőlegese, a

C

pontot most is kizárva belőle.

Nagy Sándor

2. megoldás. Alkalmazzuk a 2. feladatot, és rajzoljuk meg a

C

-n átmenő,

A

-t

B

-be vivő inverzió egyértelműen meghatározott alapkörét,

k

-t (ha

A C = B C

, akkor

A B

felező merőlegesével helyettesítsük

k

-t). Ha az inverzió centruma

k

-nak

C

-től különböző pontja, akkor

k

inverze egyenes lesz, melyre

A'

és

B'

tükrösen helyezkednek el (lásd 31. probléma), tehát az inverzió a kívánt tulajdonságú. Ha az inverzió középpontja nincs a

k

-n, akkor

k

inverze kör, melyre

A'

és

B'

inverz pont pár, de ekkor

A' C' = B' C'

nem teljesülhet, mert ekkor ilyen kör nincs a 2. feladat szerint. A mértani helyet tehát

k

-nak

C

-től különböző pontjai alkotják.

Petz Dénes

5. feladat. Adott egy tetszőleges háromszög. Van-e olyan inverzió, mely a háromszög csúcsaihoz egy szabályos háromszög csúcsait rendeli hozzá?

Megoldás. A 4. feladat megadja azon

O

inverzió középpontok mértani helyét, melyekre invertálva (tetszőleges sugár esetén)

A' C' = B' C'

, s láttuk, hogy ez a mértani hely a 3. feladatban szereplő

k_{c}

kör (melyet az

A B

felező merőlegesével kell pótolni, ha

A C = B C

). Az

A' B' = B' C'

feltételhez tartozó kör hasonlóan a 3. feladat

k_{b}

köre. Ezek metszéspontjára és csak erre teljesül a feladat követelménye. Láttuk, hogy ezek a körök a háromszög Miguel-pontjaiban metszik egymást, ezek és csak ezek a megfelelő inverziócentrumok. Ha a két mértani hely egyike egyenes, ez a mondottakon nem változtat; ha kettő egyenes, akkor már a kiindulási háromszög is egyenlő oldalú, tehát a harmadik mértani hely is egyenes, és csak egyetlen ilyen pont létezik, a háromszög középpontja.

Megjegyzés. Az 5. feladat és a 3. feladat egymás ,,inverzei''. A

k_{a}

k_{b}

k_{c}

metszéspontja körüli körre invertálva, az

A B C

háromszög szabályos háromszögbe megy át, és

k_{a}'

k_{b}'

k_{c}'

ennek magasságvonalai lesznek. Megfordítva, ha egy inverzió az

A B C

háromszöget szabályos háromszögbe viszi, ez utóbbi magasságvonalait visszainvertálva a kívánt tulajdonságú

k_{a}

k_{b}

k_{c}

, köröket kapjuk, melyek nyilván átmennek az inverzió centrumán.

Sebő András

6. feladat. Adott a síkban két kör,

k_{1}

és

k_{2}

, melyek nem metszik egymást és egyik sincs a másik belsejében. Mutassuk meg, hogy két olyan pont van a síkban, melyek körül tetszőleges

k

kört rajzolva, a

k_{1}

és

k_{2}

körök k-ra vonatkozó

k_{1}'

k_{2}'

inverzei koncentrikus körök.

Megoldás. Tegyük még fel, hogy a két kör nem is érinti egymást, mert különben nem lehet a feladatnak megoldása, hiszen az inverzek is érintenék egymást.
Vegyünk fel egy

k

kört, mely

k_{1}

-et és

k_{2}

-t merőlegesen metszi és

c

centrálisukat is két pontban metszi. Legyen a két metszéspont

P_{1}

és

P_{2}

. Ilyen például az egyik közös belső érintő fölé emelt Thalész-kör (5. ábra).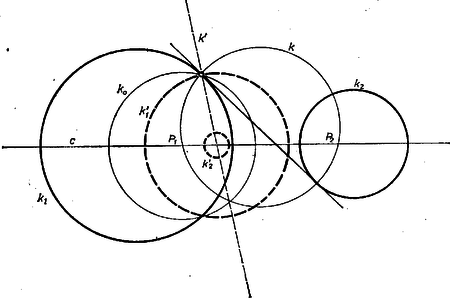

5. ábra

Megmutatjuk, hogy

P_{1}

P_{2}

bármelyike megfelel a feladat követelményeinek. Pl. a

P_{1}

körüli

k_{0}

körre invertálva, a

k'

és

c' \equiv c

egyenesek merőlegesen metszik

k_{1}'

-et és

k_{2}'

-t, tehát középpontjukon áthaladnak.

k'

és

c

metszéspontja lesz tehát mindkét kör középpontja, tehát koncentrikusak.
Több ilyen pont nincs, mert valamely

P_{3}

pontra invertálva

k'

és

c'

közül legalább az egyik kör lenne, és olyan kör, amely a koncentrikus

k_{1}'

-t és

k_{2}'

-t merőlegesen metszi, nem létezik.

Balog János

7. feladat. Adott a síkban két kör, melyeknek van közös belső érintőjük. Mutassuk meg, hogy van két pont a síkban, melyeken, körök tetszőleges közös (külső vagy belső) érintőjének az érintési pontok közti szakasza fölé rajzolt Thalész-kör átmegy.

Megoldás. Tegyük fel, hogy a két kör (

k_{1}

és

k_{2}

) nem érinti egymást. (Érintő körök esetén a feladat állításában szereplő két pont az érintési ponttal esik össze.) A feladat állításán túlmenően azt bizonyítjuk be, hogy tetszőleges, a

k_{1}

-et és

k_{2}

-t merőlegesen metsző

k

kör átmegy a 6. feladat által meghatározott két ponton. Invertáljunk ezen pontok valamelyike körüli körre:

k_{1}'

k_{2}'

koncentrikusak lesznek,

k'

ezeket merőlegesen metsző kör vagy egyenes. Koncentrikus köröket merőlegesen metsző kör nem létezik, tehát

k'

egyenes, azaz

k

átmegy az inverzió centrumán, s ezt akartuk bizonyítani.

Petz Dénes Balog János

A 8. feladat megoldását vázlatosan a 9. feladat 1. megoldásába olvasztottuk bele.

9. feladat. (Euler tétele). Bizonyítsuk be, hogy két adott körhöz (

k

-hoz és

k_{1}

-hez) akkor és csakis akkor van olyan háromszög, melynek

k

a körülírt,

k_{1}

a beírt köre, ha

\begin{matrix} d^{2} + r_{1}^{2} = {(r - r_{1})}^{2}, \end{matrix}

(4)

ahol

r

r_{1}

k

és

k_{1}

körök sugara,

d

pedig a középpontjaik távolsága.

1. megoldás. Először Euler tételének a következő átfogalmazását bizonyítjuk be: a sík

k

és

k_{1}

köreihez akkor és csakis akkor létezik olyan

A B C

háromszög, amelynek

k

a körülírt,

k_{1}

a beírt köre, ha

k_{1}

k

belsejében van, és

k

-nak

k_{1}

-re vonatkozó

k'

inverzében az átmérő egyenlő

k_{1}

sugarával.
Tegyük fel, hogy létezik ilyen

A B C

háromszög, akkor

k_{1}

nyilván

k

belsejében van. Érintse

k_{1}

a háromszög oldalait az

A_{1}

B_{1}

C_{1}

pontokban, és jelöljük

k_{1}

középpontját

O_{1}

gyel (6. ábra).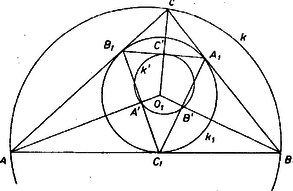

6. ábra

Könnyen látható, hogy az inverzió alapkörére nézve tetszőleges külső pont inverzét megkaphatjuk úgy is, hogy az illető pontból érintőket húzunk az alapkörhöz, és megfelezzük az érintési pontok által meghatározott szakaszt. Emiatt az

A

B

C

pontnak a

k_{1}

körre vonatkozó

A'

B'

C'

inverze rendre a

B_{1} C_{1}

C_{1} A_{1}

A_{1} B_{1}

szakasz felezőpontja, és

k

-nak

k_{1}

-re vonatkozó

k'

inverze az

A' B' C'

háromszög körülírt köre. Mivel az

A' B' C'

háromszöget az

A_{1} B_{1} C_{1}

háromszögből előállíthatjuk az

A_{1} B_{1} C_{1}

háromszög

S_{1}

súlypontjára mint centrumra vonatkozó

^{1} /_{2}

arányú kicsinyítéssel, és egy ezt követő,

S_{1}

-re vonatkozó tükrözéssel (7. ábra), azért

k'

sugara valóban fele

k_{1}

sugarának.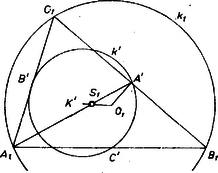

7. ábra

k_{1}

k

belsejében van, akkor

k

-nak

k_{1}

-re vonatkozó

k'

inverze

k_{1}

belsejében van. Megmutatjuk, hogy ha

k'

sugara egyenlő,

k_{1}

sugarának a felével, akkor

k'

tetszőleges

A'

pontjához található

k_{1}

-en olyan

A_{1}

B_{1}

C_{1}

és

k'

-n olyan

B'

C'

pont, hogy

A'

B'

C'

rendre felezi a

B_{1} C_{1}

C_{1} A_{1}

A_{1} B_{1}

szakaszt. Ebből pedig következik, hogy például

A'

-nek

k_{1}

-re vonatkozó

A

inverze olyan pont, hogy az

A B_{1}

A C_{1}

egyenesek érintik

k_{1}

-et, vagyis az

A'

B'

C'

pontokat

k_{1}

-re invertálva, a kapott

A B C

háromszögnek

k_{1}

a beírt köre (és természetesen

k

a körülírt köre). Ezzel tehát azt látjuk be, hogy ha

k_{1}

k

belsejében van, és

k'

átmérője egyenlő

k_{1}

sugarával, akkor létezik olyan

A B C

háromszög, amelynek

k_{1}

a beírt és

k

a körülírt köre, és ennek a háromszögnek az egyik csúcsa

k

-n tetszőlegesen felvehető.
Legyen tehát

k'

k_{1}

belsejében,

k'

átmérője legyen egyenlő

k_{1}

sugarával, és

A'

legyen

k'

tetszőleges pontja (7. ábra). Jelöljük

k_{1}

és

k'

középpontját

O_{1}

-gyel és

K'

-vel, az

O_{1} K'

szakasz

K'

-höz közelebbi harmadolópontját

S_{1}

gyel. Az

S_{1}

centrumú,

2 : 1

arányú hasonlóság, és az ezt követő,

S_{1}

-re vonatkozó tükrözés

K'

-t

O_{1}

-be,

k'

-t

k_{1}

-be viszi, tehát

A'

-t

k_{1}

valamely pontjába viszi, jelöljük ezt a pontot

A_{1}

-gyel. Emeljünk merőlegest az

A' O_{1}

szakasz

A'

végpontjában a szakaszra (feltevéseink szerint

O_{1}

k'

-nek belső pontja, tehát nem lehet

A'

-vel azonos), és messe ez a merőleges

k_{1}

-et a

B_{1}

C_{1}

pontokban. Így

A'

felezi a

B_{1} C_{1}

szakaszt, az

A_{1} B_{1} C_{1}

háromszögben

A_{1} A'

súlyvonal, és

S_{1}

súlypont. Emiatt a

B_{1}

C_{1}

pontoknak az

S_{1}

centrumú,

1 / 2

arányú kicsinyítésből, majd az ezt követő,

S_{1}

-re vonatkozó tükrözésből származó

B'

C'

képei

k'

-n vannak, és rendre felezik az

A_{1} C_{1}

A_{1} B_{1}

szakaszokat. Megoldásunk utolsó lépéseként megmutatjuk, hogy (4) akkor és csakis akkor teljesül, ha

k_{1}

k

belsejében van, és

k'

sugara

(1 / 2) r_{1}

. Legyen

k

és

k_{1}

középpontja

K

és

O_{1}

, és messe az

O_{1} K

szakaszra

O_{1}

-ben emelt merőleges

k_{1}

-et

O_{2}

-ben és

O_{3}

-ban (ha

O_{1}

azonos

K

-val,

O_{2}

és

O_{3}

legyen

k_{1}

tetszőleges két átellenes pontja), és legyen

k_{2}

, ill.

k_{3}

O_{2}

, ill.

O_{3}

középpontú,

r_{1}

sugarú kör. (4) nyilván ekvivalens azzal az állítással, hogy

k_{2}

és

k_{3}

belülről érint: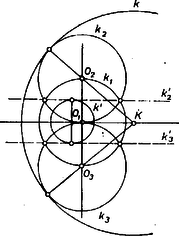

k

-t (8. ábra).

8. ábra

k_{2}

k_{3}

körök

k_{1}

-re vonatkozó

k_{2}'

k_{3}'

inverzei párhuzamos egyenesek, melyek távolsága egyenlő

k_{1}

sugarával,

k'

középpontja pedig rajta van az

O_{1}

-en átmenő, velük párhuzamos egyenesen. Tehát

k'

akkor és csakis akkor érinti a

k_{2}'

k_{3}'

egyeneseket, ha az átmérője egyenlő

k_{1}

sugarával. Állításunkat ezzel bebizonyítottuk.

2. megoldás¹. Megmutatjuk, hogy a

k

belsejében levő

O_{1}

pont akkor és csak akkor egyezik meg valamely, a

k

-ba beírt

A B C

háromszög beírható körének középpontjával, ha

O_{1} P = P C

, ahol

P

A

-t nem tartalmazó

B C

ív felezőpontját jelöli. Jelöljük a háromszög szögeit

α

β

γ

-val (9. á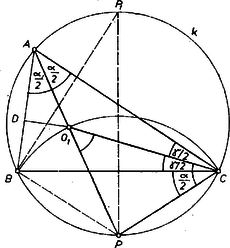bra).

9. ábra

Tegyük fel, hogy

O_{1}

a beírt kör középpontja, akkor

O_{1}

rajta van a

C ∢

szögfelezőjén,

C O_{1} P ∢ = (α / 2) + (γ / 2)

, mert az

A O_{1} C

háromszög külső szöge, az

O_{1} C P ∢ = (α / 2) + (γ / 2)

, mert a

B C P ∢ = B A P ∢ = α / 2

, tehát az

O_{1} P C

háromszög egyenlő szárú, azaz

O_{1} P = P C

. Fordítva, ha

O_{1} P = P C

, akkor, mivel a beírt kör

O_{1}'

középpontja rajta van

A P

-n, és arra

O_{1}' P = P C

, nyilván következik, hogy

O_{1}' \equiv O_{1}

.
Rajzoljuk meg még a

P P_{1}

átmérőt és jelöljük

D

-vel az

A B

és

k_{1}

érintési pontját, akkor

A D O_{1} ▵ \sim P_{1} B P ▵

, amiből

A O_{1} : r_{1} = 2 r : P B

, azaz

2 r r_{1} = A O_{1} \cdot P B = A O_{1} \cdot O_{1} P

, s ez utóbbi a szelők tétele értelmében

(r + d) (r - d)

-vel egyenlő. Azaz a beírt kör sugarát az

A

pont helyzetétől függetlenül a

2 r r_{1} = (r + d) (r - d)

egyenlet határozza meg, s ezt akartuk bizonyítani.

Pap Gyula

10. feladat. A III. példához kapcsolódva mutassuk meg, hogy ha

d ⊥ c

, akkor

O_{1}

felezi az

O_{2} O_{3}

szakaszt. (A III. példa szövegét lásd alább.)

Megoldás. Jelöljük a két kör másik közös érintőjét

c_{1}

-gyel,

c_{1}

és

d

metszéspontját

P

-vel. A III. példából az

O_{1}

-et úgy kaphatjuk meg, hogy

P

-t merőlegesen vetítjük

O_{2} O_{3}

-ra.

P O_{2} ⊥ P O_{3}

, mivel a

d

és

c_{1}

egyenesek szögfelezői. Jelöljük a

c

és

c_{1}

egyenesek metszéspontját

Q

-val (ha

c

és

c_{1}

párhuzamosak, az állítás szimmetriaokokból nyilvánvaló), a

P Q D

szöget

2 φ

-vel, akkor

Q P D ∢ = 90^{\circ} - 2 φ

O_{1} P D ∢ = φ

(merőleges szárú szögek),

O_{2} P O ∢ = 45^{\circ}

, tehát az

O_{2} P O_{3}

háromszög derékszögű egyenlő szárú háromszög, amiből az állítás következik.

Boros Endre

Beszámolónk utolsó része a III. példa elemi megoldásának a közlése.

III. példa (az 1969. évi Nemzetközi Matematikai Diákolimpia 4. feladatának általánosítása). Legyen az

A B C

háromszög körülírt kőre

k

, beírt köre

k_{1}

, az

A B

szakasz tetszőleges belső pontja

D

. Jelöljük az

A B

egyenest

c

-vel, a

D C

félegyenest

d

-vel (10. ábra). A

c

egyenest,

k

kört és a

d

félegyenest érintő két kör legyen

k_{2}

és

k_{3}

. Megmutatjuk, hogy
a) a

k_{1}

k_{2}

és

k_{3}

kör

O_{1}

O_{2}

O_{3}

középpontja egy egyenesen van,
b) a

k_{1}

kört a

k_{2}

k_{3}

körök és a

d

félegyenes egyértelműen meghatározzák.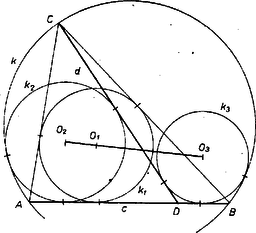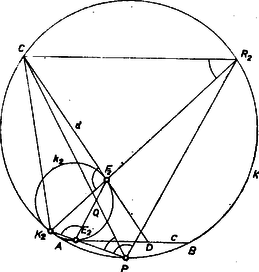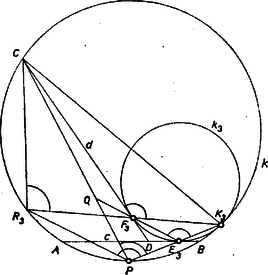

10. ábra

Bizonyítás. A

C

pontot nem tartalmazó

A B

ív felező pontját jelöljük

P

-vel, a

c

és

d

egyenesek és a

k_{2}

kör érintési pontjait pedig

E_{2}

F_{2}

-vel.

E_{2} F_{2}

és

C P

metszéspontja legyen

Q

(

11 a

és

11 b

ábra).

11a. ábra

11b. ábra

Először bebizonyítjuk, hogy

Q

mindig létezik, azaz

P C

és

E_{2} F_{2}

nem lehetnek párhuzamosak. Jelöljük a

k

és

k_{2}

körök érintési pontját

K_{2}

-vel,

K_{2}

egyben e két kör hasonlósági középpontja is: E hasonlóságnál

E_{2}

és

P

egymásnak megfelelő pontok, hiszen a

k

-hoz

P

-ben húzható érintő párhuzamos

A B

-vel, és az

A B

egyenes elválasztja a

K_{2}

és

P

pontokat. Ha

P C | | E_{2} F_{2}

lenne, akkor

F_{2}

-nek e nagyítás során

C

felel meg, azaz

K

F_{2}

és

C

egy egyenesbe esnek, de ez ellentmondás, hiszen

C F_{2}

k_{2}

kör érintője kellene legyen.
Bizonyításunk második lépéseként, felhasználva a 9. feladat 2. megoldását, meg fogjuk mutatni, hogy

Q \equiv O_{1}

Ehhez először számítsuk ki a

P Q

szakasz hosszát. Bővítsük ki az ábrát: a

K_{2} F_{2}

egyenes messe

k

-t

R_{2}

-ben. Be fogjuk bizonyítani, hogy

P E_{2} Q ▵ \sim R_{2} F_{2} C ▵ \sim R_{2} C K_{2} ▵

. Mindhárom háromszögnek

P

-nél, ill.

R_{2}

-nél levő szögei, azonos íven nyugvó kerületi szögek lévén, egyenlők. Ezután a

P E_{2} Q ∢

R_{2} F_{2} C ∢

és

R_{2} C K_{2}

szög kiegészítő szögeinek egyenlőségét látjuk be:

K_{2} E_{2} Q ∢ = K_{2} F_{2} C ∢

, mert azonos íveken nyugvó kerületi szögek,

K_{2} E_{2} Q ∢ = K_{2} P R_{2} ∢

, mert

E_{2} F_{2} | | P R_{2}

, ugyanis

O

hasonlósági középpont, továbbá a

K_{2} P R_{2} ∢ = 180^{\circ} - R_{2} C K_{2} ∢

, mert

P K_{2} C R_{2}

húrnégyszög. A párhuzamos szelők tételét, majd az első két háromszög hasonlóságát felhasználva

\begin{matrix} P K_{2} : R_{2} K_{2} = P E_{2} : R_{2} F_{2} = P Q : R_{2} C . \end{matrix}

Két oldal aránya és egy szög megegyezik, tehát

P Q K_{2} ▵ \sim R_{2} C K_{2} ▵

. Az előzőkkel egybevetve

P E_{2} Q ▵ \sim P Q K_{2} ▵

, amiből

P E_{2} : P Q = P Q : P K_{2}

, azaz

P Q

mértani középarányos

P E_{2}

és

P K_{2}

között. Másrészt

P E_{2} A ▵ \sim P A K_{2} ▵

, mert egy szög közös és

E_{2} A P ∢ = A K_{2} P ∢

, ugyanis egyenlő íveken nyugvó kerületi szögek. Ebből

P E_{2} : P A = P A : P K_{2}

, azaz

P A

mértani középarányos

P E_{2}

és

P K_{2}

között, így

P A = P Q

. Alkalmazva a 9. feladat elemi bizonyításában szereplő első állítást,

Q

A B C

háromszög beírt körének középpontja, azaz

Q \equiv O_{1}

.
Ugyanezt elmondhatjuk a

k_{3}

és

k

körre vonatkozólag is (a kettes indexeket hármasra felcserélve). Ez azt jelenti, hogy

E_{3} F_{3}

is átmegy

Q_{1}

-en, azaz

E_{2} F_{2}

és

E_{3} F_{3}

metszéspontja adja

Q_{1}

- et. Ezzel a b) állítást már igazoltuk, mivel az

E_{2}

E_{3}

F_{2}

F_{3}

pontok függetlenek a

k

kör választásától.
Tekintsük most a 12. ábrát.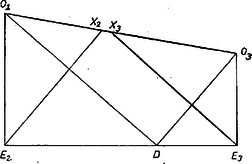

12. ábra

Be kell bizonyítani, hogy

E_{2} F_{2}

és

E_{3} F_{3}

Q_{2} O_{3}

-on metszik egymást.

O_{2} D ⊥ O_{3} D

E_{2} F_{2} ⊥ O_{2} D

és

E_{3} F_{3} ⊥ O_{3} D

, mivel

O_{2} D

és

O_{3} D

c

és

d

egyenesek szögfelezői. Messe

E_{2} F_{2}

O_{2} O_{3}

-t

X_{2}

-ben, továbbá

E_{3} F_{3}

metszéspontja

O_{2} O_{3}

-mal legyen

X_{3}

. Mivel

O_{2} E_{2} D ▵ \sim D E_{3} O_{3} ▵

, a magasságvonalak ugyanolyan arányban osztják az átfogót mindkét háromszögben. A párhuzamos szelők tétele szerint azonban ugyanilyen arányban osztja

X_{2}

is és

X_{3}

O_{2} O_{3}

-t, tehát

X_{2} \equiv X_{3}

, s ezt akartuk bizonyítani.

¹Lásd K. M. L. 42 (1971) 1-7.

²Lásd K. M. L. 43 (1971) 5‐6.

¹Lásd a megoldást K. M. L. 39 (1969) 155-166.

¹ Ez a megoldás megtalálható Kürschák J. ‐ Hajós Gy. ‐ Neukomm Gy. ‐ Surányi J.: Matematikai versenytételek, I. rész. 3. kiadás. Tankönyvkiadó. Budapest. 1965. 40‐41.