Cím: 1970. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Lovász László 
Füzet: 1971/május, 193 - 198. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Legfeljebb hány hegyesszöge lehet egy (önmagát nem metsző) síkbeli n-szögnek?

 
Megoldás. Jelölje k a sokszög hegyesszögeinek számát. Mivel minden hegyesszög kisebb, mint 90∘, a hegyesszögek összege kisebb, mint k⋅90∘. A többi n-k szögről csak annyit tudunk, hogy kisebbek, mint 360∘, így összegük kisebb, mint (n-k)⋅360∘. Így az n-szög szögösszege kisebb, mint
k⋅90∘+(n-k)⋅360∘=n⋅360∘-k⋅270∘.
Másrészről azonban az n-szög szögeinek összege (n-2)⋅180∘, tehát
(n-2)⋅180∘<n⋅360∘-k⋅270∘,
ahonnan rendezés és 90∘-kal való osztás után
3k≤2n+4
adódik. Mivel mindkét oldalon egész szám áll,
3k≤2n+3,
és így
k≤2n3+1.
Így azt kaptuk, hogy egy síkbeli n-szögnek legfeljebb
[2n3]+1
hegyesszöge lehet (a szögletes zárójel, mint szokásos, a szám egész részét jelöli).
Hozzátartozik még a feladathoz annak megmutatása, hogy ez a korlát el is érhető; más szóval, olyan n-szöget kell konstruálnunk, melyben a hegyesszögek száma pontosan [2n3]+1.
Foglalkozzunk először azzal az esettel, amikor n3-mal osztható, vagyis n=3r. Ekkor [2n3]+1=2r+1.
 
 

1. ábra
 

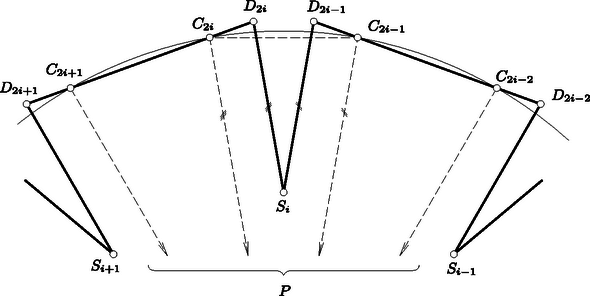
Tekintsünk egy 60∘-os körcikket, legyen a körív két végpontja A és B, a körcikk csúcsa P, és osszuk az AB ívet a C1, C2,...,C2r-2 pontokkal 2r-1 egyenlő részre. Jelölje Si a C2i-1PC2i háromszög súlypontját (i=1,...,r-1). Húzzunk Si-n át párhuzamost PC2i-1-gyel, és messe ez a C2i-2C2i-1 egyenest D2i-1-ben, C0-on A-t értve. Hasonlóképpen legyen D2i a PC2i-vel párhuzamos, Si-n áthaladó egyenesnek és C2iC2i+1-nek metszéspontja, C2r-1-en B-t értve (1. ábra). Tekintsük mármost a következő sokszöget:
Σ=PAD1S1D2D3S2D4...D2i-1SiD2iD2i+1Si+1...D2r-3Sr-1D2r-2BP
(2. ábra). Ennek nyilván 3r csúcsa van és 2r+1 hegyesszöge a P, A, D1, D2,...,D2r-2, B csúcsok mindegyikénél hegyesszöge van. Ugyanis az APB szög 60∘, a PAD1 szög a PAC1 egyenlő szárú háromszög alapján fekvő szögek egyike, tehát hegyesszög, az AD1S1 szög pedig ezzel egyenlő, hiszen AD1S1 és AC1P párhuzamos szárú szögek. A többi felsorolt szögről hasonlóan látható be, hogy hegyesszögek.
 
 

2. ábra
 

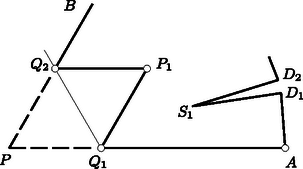
Másodszor azzal az esettel foglalkozunk, amikor n3-mal osztva 1-et ad maradékul, vagyis n=3r+1. Ekkor [2n3]+1=2r+1. Az előzőek szerint tudunk olyan 3r-szöget szerkeszteni, melynek 2r+1 hegyesszöge van. Tekintsük az előzőekben megszerkesztett Σ sokszöget, és az AP oldal felező merőlegesén válasszunk egy olyan Q pontot, mely benne van a PAC1 háromszögben. Ekkor QAC1∢<PAC1∢ és QPB∢<APB∢, tehát hegyesszögek, így a Σ sokszög AP oldalát az AQP töröttvonallal helyettesítve olyan Σ' (3r+1)-szöget kapunk, melyben 2r+1 hegyesszög van (3. ábra).
 
 

3. ábra
 

Végül tekintsük az n=3r+2 esetet. Tekintsük ismét a 3r csúcsú Σ sokszöget. Legyen PA, ill. PB(P-hez közelebbi) harmadolópontja Q1, ill. Q2, és P-nek Q1Q2-re való tükörképe P1. Ekkor a Σ sokszög AP, PB oldalait az AQ1P1Q2B töröttvonallal helyettesítve olyan Σ'' sokszöget kapunk, melynek 3r+2 csúcsa és 2r+2=[2n3]+1 hegyesszöge van, hiszen a P helyett fellépő három csúcs közül kettőben, Q1-ben és Q2-ben 60∘-os, vagyis hegyesszög van (4. ábra).
 
 

4. ábra
 

 
Megjegyzések. 1. Az olvasóra bízzuk annak belátását, hogy a Σ, Σ', Σ'' sokszögek nem metszik át önmagukat.
2. Számos más módon is konstruálható n szögpontú, [2n3]+1 hegyesszöggel rendelkező sokszög. Több versenyző teljes indukcióval definiálta ezeket, n-ről n+3-ra lépve (ekkor n=3, 4, 5 esetére meg kell adni egy-egy példát, ami nyilvánvaló). A legtöbb megoldásban Σ a fentihez hasonlóan volt megalkotva, de belőle Σ'-t és Σ''-t már igen sok különböző módon készítették el a versenyzők.
3. Több versenyző megjegyezte, hogy ha csak konvex sokszögekre szorítkoznánk, a hegyesszögek maximális száma 3 volna.
 
Második feladat. Mi a valószínűsége annak, hogy egy lottóhúzás öt száma között van legalább két szomszédos (amelyek különbsége 1)?
 
I. Megoldás. Jelölje p a kérdezett valószínűséget, k pedig az első 90 számból kiválasztható azon számötösök számát, melyekben nincsen két szomszédos. Mivel az összes lehetséges lottóhúzások száma (905), azért
p=1-k(905),
így tulajdonképpen a k szám meghatározása a feladat.
Tekintsünk egy olyan
1≤a<b<c<d<e≤90
számötöst, melyben nincs két szomszédos azám. Ekkor az
a,b-1,c-2,d-3,e-4
számötös számai különbözők, és 1 és 86 közé esnek. Megfordítva, minden
1≤a'<b'<c'<d'<e'≤86
számötös esetén
a',b'+1,c'+2,d'+3,e'+4
olyan számötös, melynek mindegyik eleme 1 és 90 közé esik, és nem tartalmaz szomszédos számokat. Így k egyenlő az első 86 számból kiválasztható számötösök számával, vagyis
k=(865).
Innen
p=1-(865)(905)=1-86⋅85⋅84⋅83⋅8290⋅89⋅88⋅87⋅86=0,2...
 
II. Megoldás. Az előző megoldásban talált k számot más ötlettel is meghatározhatjuk. Tekintsünk egy sorban 90 egyforma golyót, egy kicsit ferde vályúban és emeljük ki az a-adikat, b-ediket, c-ediket, d-ediket és e-ediket, ahol a, b, c, d, e egy olyan lottószámötös, amely nem tartalmaz szomszédos egészeket. A visszamaradó golyók összegurulnak, és egy 85 golyóból álló láncot alkotnak. k mármost annak számát jelenti, ahányféleképpen 5 nem szomszédos golyót a 90-ből ki lehet emelni; vagyis, megfordítva, ahányféleképpen a 85 golyóból álló láncba 5 golyót be tudunk iktatni úgy, hogy ne legyen közöttük két szomszédos. Egy ilyen ,,beiktatást'' azzal jellemezhetünk, hogy megmondjuk, a lánc 86 ,,golyóköze'' közül melyik 5-öt választjuk ki (a lánc eleje és vége is ,,köz''-nek számít, ezért 86 a számuk). Vagyis
k=(865).

Megjegyzések. 1. Ha n számból m-et húzunk, akkor annak a valószínűsége, hogy a kihúzott számok között van legalább két szomszédos:
1-(n-m+1m)(nm).

2. Az első megoldás gondolatmenete segítségével az is belátható (ez az általánosítás Ruzsa Imre dolgozatában szerepelt), hogy ha megadunk c1, c2,...,cm-1 természetes számokat, akkor annak a valószínűsége, hogy az első n természetes számból kihúzott 1≤a1<...<am≤n szám-m-esre
a2-a1>c1,a3-a2>c2,...,am-am-1>cm-1
álljon fenn, éppen
(n-c1-c2-...-cm-1m)(nm).
Ennek belátásához azt jegyezzük meg, hogy ha (a1,...,am) ilyen szám-m-es, akkor
1≤a1<a2-c1<a3-c1-c2<...<am-c1-c2-...-cm-1≤n-c1-...-cm-1,
és viszont.
3. A magyar lottóhúzások 1957-től 1971. március végéig lefolyt 738 húzása közül 146-ban fordult elő a vizsgált számszomszédosság, éspedig a számötösöket növekvően rendezve az 1. és 2. helyen álló számok között 39 esetben, a további szomszédos helyek között rendre 27, 41, 39 esetben.
 
Harmadik feladat. Adva van n pont, amelyek közül semelyik három sincs egy egyenesen. Az általuk meghatározott szakaszok közül néhányat pirossal, néhányat kékkel rajzoltunk be úgy, hogy a megszínezett szakaszok mentén haladva bármelyik pontból bármelyik pontba el lehessen jutni, de csak egyféleképpen. Bizonyítandó, hogy a pontok által meghatározott, még meg nem színezett szakaszok kifesthetők kékre vagy pirosra úgy, hogy az adott pontok által meghatározott bármelyik háromszög oldalai között páratlan számú piros legyen.
 
I. Megoldás. Megadunk egy utasítást arra, hogyan kell a még nem színezett szakaszokat színezni. Legyen AB egy olyan szakasz, amelynek végpontjai az adott pontok közül valók és amely még nincs kiszínezve. A feltétel szerint létezik egy és csakis egy olyan törött vonal, mely eredetileg színezett szakaszokból áll és A-t B-vel köti össze. Jelölje VAB ezt a törött vonalat. Legyen mármost az AB szakasz
 
kék, ha VAB páratlan sok kék szakaszt tartalmaz és legyen
piros, ha VAB páros sok kék szakaszt tartalmaz.
 

(Megjegyezzük, hogy ez a ,,színezési szabály'' akkor is érvényes, ha AB már eleve is színezett volt.)
Megmutatjuk, hogy a fenti ,,színezési szabály'' kielégíti a feladat követelményeit. Legyen e célból ABC tetszőleges háromszög, melynek csúcsai az adott pontok közül valók.
Először is megadható olyan D pont, melyből az A-ba, B-be, C-be vezető, eredetileg színezett szakaszokból álló VDA, VDB, VDC utaknak nincsen D-től különböző közös pontjuk (megengedjük itt, hogy D egybeessen pl. A-val, ekkor VDA egyetlen pontból áll). Tekintsük ugyanis az A-t B-vel összekötő, eredetileg színezett szakaszokból álló VAB utat. C-ből A felé elindulva a VCA úton, előbb-utóbb elérjük a VAB út valamely D pontját (ha C rajta fekszik a VAB úton, akkor D=C; természetesen az is előfordulhat, hogy D=A vagy D=B). Könnyen látható, hogy az így megszerkesztett D pont a fenti kikötésnek eleget tesz (5. ábra).
 
 

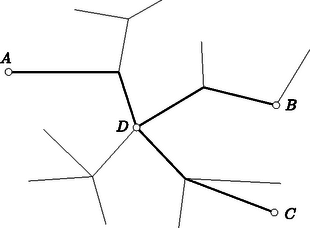5. ábra
 

Mármost a fenti színezési szabály szerint, az AB, BC, AC szakaszok között rendre annyi kék van, ahány páratlan szám előfordul az
 
x=a  VDA és VDB utakon fekvő kék szakaszok száma,
y=a  VDB és VDC utakon fekvő kék szakaszok száma és
z=a  VDC és VDA utakon fekvő kék szakaszok száma között.
 

Mivel x+y+z páros (hiszen VDA, VDB, VDC utak minden kék szakasza kétszer van beszámítva ebbe az összegbe), az ABC háromszögnek valóban páros sok kék oldala van.
 
II. Megoldás. Válasszunk ki egy tetszőleges A0 pontot és színezzük ki sárgára. Ezek után a többi pontot is kiszínezzük sárgával és zölddel a következőképpen: egy A0-ból kiinduló, eredetileg is színezett szakaszokból álló törött vonal mentén haladva, az i-edik pont legyen az (i-1)-edikkel azonos színű, ha a kettőt összekötő szakasz piros, és különböző színű, ha az összekötő él kék. Mivel a feltétel szerint bármely pontba egy és csakis egyféleképpen juthatunk el ilyen törött vonalon, azért minden pont színe egyértelműen meg van határozva.
Ezek után a következő ,,színezési szabályt'' adhatjuk meg: az AB él legyen
 
piros, ha A, B mindegyike zöld vagy mindegyike sárga, és legyen
kék, ha A, B különböző színűek.
 
Megállapíthatjuk, hogy az eredetileg megszínezett szakaszok e ,,színezési szabálynak'' megfelelően vannak színezve.
Tekintsünk mármost egy tetszőleges ABC háromszöget, melynek csúcsai az adott pontok közül valók. Ha A, B, C azonos színűek, akkor az AB, BC, AC szakaszok mindegyike piros. Ha, mondjuk A és B azonos és C tőlük különböző színű, akkor AB piros, AC és BC kék. A piros szakaszok száma tehát vagy 3 vagy 1, mindenképpen páratlan. Tehát a megadott ,,színezési szabály'' a feladat kikötésének eleget tesz.
 
Megjegyzések. 1. Több dolgozat a pontok száma szerinti teljes indukcióval igazolta az állítást.
2. Megmutatható ‐ erre több versenyző utalt is ‐, hogy a szakaszoknak a feladatbeli színezése egyértelmű. Legyen ugyanis AB tetszőleges szakasz. A feltétel szerint A és B összeköthető egy, eleve színezett élekből álló
A0A1...An¯(A0=A,An=B)
törött vonallal. Mármost az A0A1A2 háromszögben páratlan sok piros élnek kell lennie, ez meghatározza az A0A2 szakasz színét. Így az A0A2A3 háromszögben már két szakasz színe adott, ez meghatározza az A0A3 szakasz színét. Hasonlóan továbbmenve láthatjuk, hogy az AB szakasz színe is egyértelműen meg van határozva.
3. Elegendő volna a feladatban annyit feltenni, hogy bármely két pont legfeljebb egyféleképpen köthető össze eredetileg is megszínezett szakaszokból álló törött vonallal. Ilyenkor ugyanis (mint az könnyen igazolható) meg lehet még néhány további szakaszt színezni úgy, hogy a kapott szakaszokra már a feladat feltétele teljesüljön.