Kezdőlap


Cím:	Vektorok felhasználása egy bizonyos típusú bűvös kövezetek vizsgálatában (megjegyzések az 1572. számú feladathoz)
Szerző(k):	Bakos Tibor
Füzet:	1971/március, 97. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1572. feladatban^{$^{*}$} tetszés szerinti $n$ páratlan oldalszám esetére nem döntöttük el, hogy a bélyegzővel előállított bűvös kövezet pándiagonális, azaz minden átlójában bűvös-e, vagy csak némely átlóiban, vagy hogy egyáltalán lehet-e a kövezetben bűvös négyzetet kijelölni a keret alkalmas elhelyezésével. Ezt és az ottani egyéb kérdéseket is más eljárással újra vizsgáljuk.

1. Valamivel kényelmesebb, ha a szokásos

1,2, ..., n^{2}

számok helyett az

1

-gyel kisebb

0,1, ... (n^{2} - 1)

számokat írjuk be bélyegzőnkre, mert ezek az

n

-alapú számrendszernek éppen az összes kétjegyű számai:

\begin{matrix} \bar{a b} = a n + b, \end{matrix}

ahol

a

-ra,

b

-re egyformán

\begin{matrix} 0 ≦ a, b ≦ n - 1. \end{matrix}

(1)

Pl. az 1572. feladat 1. ábráján az

1

-estől jobbra fölfelé haladó bejegyzések helyére rendre ezek lépnek:

\begin{matrix} \bar{00}, \bar{01}, \bar{02}, ..., \bar{0, n - 2}, \bar{0, n - 1} . \end{matrix}

2. Helyezzünk a lenyomatok papirosára szokásos koordináta-rendszert, origójának a

\bar{00}

szám első lenyomatbeli példányát, tengelyirányoknak a sorok, ill. oszlopok irányát, hosszúságegységnek pedig egy kis mező oldalát véve. Legyen még a jobbra és a fölfelé mutató egységvektor

i

, ill.

j

, ekkor az előbbi számoknak (pontosabban az őket tartalmazó mezők középpontjainak) helyvektorai rendre

\begin{matrix} 0, 2 i + j, 2 (2 i + j), ..., (n - 1) (2 i + j), \end{matrix}

\bar{00}

-ból induló, jobbra lejtő bejegyzéseké

\begin{matrix} 0, 2 i + j, 2 (2 i + j), ..., (n - 1) (2 i + j), \end{matrix}

általában az

\bar{a b}

szám első lenyomatbeli példányának helyvektora

\begin{matrix} a (2 i - j) + b (2 i + j) = 2 (a + b) i - (a - b) j, \end{matrix}

és ezen szám minden további lenyomatbeli példányának helyvektora

\begin{matrix} (2 a + 2 b + g_{1} n) i + (- a + b + g_{2} n) j \end{matrix}

(2)

alakú, ahol

g_{1}

g_{2}

egészek (úgyszintén a tovább bevezetendő

g_{i} (i = 3,4, ...)

számok is). Mindezen alakok az összegek szempontjából ekvivalensek. Azt az alakot, amelyben a (2)-beli két koordináta

0

és

n - 1

közé esik (a korlátokat beleértve), az

\bar{a b}

szám redukált helyvektorának nevezzük.

3. Megmutatjuk, hogy a lenyomatok előírt megismétléseivel sohasem áll elő két szám átfedése, más kifejezéssel: az

\bar{a b}

és

\bar{c d}

számok redukált helyvektora csak akkor egyező, ha

a = c

és

b = d

.
Az egyezés feltétele a vektorok végpontjaihoz tartozó koordináták egyenlősége:

\begin{matrix} 2 a + 2 b + g_{1} n = 2 c + 2 d + g_{3} n, \\ - a + b + g_{2} n = - c + d + g_{4} n, \end{matrix}

és ha ez teljesül, akkor

\begin{matrix} 2 (a - c) + 2 (b - d) = (g_{3} - g_{1}) n = g_{5} n, \\ - (a - c) + (b - d) = (g_{4} - g_{2}) n = g_{6} n . & (3) \end{matrix}

Mivel

n

páratlan, azért

g_{5}

páros,

g_{5} = 2 g_{7}

, és így az elsőből

\begin{matrix} (a - c) + (b - d) = g_{7} n, \end{matrix}

(4)

amit (3)-hoz hozzáadva és a legutóbbi meggondolást megismételve

\begin{matrix} 2 (b - d) = (g_{6} + g_{7}) n = 2 g_{8} n, \\ b - d = g_{8} n . \end{matrix}

Ámde két számjegyünk különbségére

\begin{matrix} - (n - 1) ≦ b - d ≦ n - 1, \end{matrix}

és e korlátok közt

n

-nek egyetlen többszöröse

0

, így

b = d

. ‐ Ugyanígy adódik (3)-ból és (4)-ből kivonással

a = c

, amint állítottuk.

4. A bélyegző által előállított kövezetben sorok, oszlopok, jobbra lejtő vagy emelkedő átlók (röviden fő-, ill. mellékátló) mentén összekerülő számok kapcsolatának meghatározása céljára kérdezzük általánosan: mely szám áll egy

\bar{c d}

számból (pontosabban mezejének középpontjából) kiinduló

x i + y j

vektor végpontjában, ahol

0 ≦ x

y ≦ n - 1

. Az eredményt

(x, y) = (1; 0)

-ra, majd

(x, 0)

-ra alkalmazva a

\bar{c d}

-től jobbra az

x

-edik (más szóval balra az

n - x

-edik) mezőn álló számot fogjuk kapni; hasonlóan

(0; 1)

és

(0; y)

esetén a vele egy oszlopban álló számokat,

(x, x)

és

(x, n - x)

esetén pedig a vele egy-egy átlós vonalon állókat, hiszen

(x, n - x)

ekvivalens

(x, - x)

-szel.
A keresett számot

\bar{a b}

-vel jelölve,

\bar{a b}

és

\bar{c d}

alkalmas lenyomataihoz tartozó helyvektorok különbségére fennáll

\begin{matrix} {(2 a + 2 b + g_{1} n) i + (- a + b + g_{2} n) j} - \\ - {(2 c + 2 d + g_{3} n) i + (- c + d + g_{4} n) j} = x i + y j, \end{matrix}

vagy rövidítésül bevezetve az

a - c = a^{*}

b - d = b^{*}

jelöléseket:

\begin{matrix} (2 a^{*} + 2 b^{*} + g_{5} n) i + (- a^{*} + b^{*} + g_{6} n) j = x i + y j, \end{matrix}

amiből

a^{*}

-ra és

b^{*}

-ra az alábbi egyenletrendszert kapjuk. (Megjegyezzük, hogy itt

- (n - 1) ≦ a^{*}

b^{*} ≦ (n - 1)

hiszen

a < c

és

b < d

is lehetséges, továbbá, hogy

a^{*}

-on,

b^{*}

-on felül tulajdonképpen a

g

számok is ismeretlenek.)

\begin{matrix} 2 a^{*} + 2 b^{*} + g_{5} n = x, \\ - a^{*} + b^{*} + g_{6} n = y . \end{matrix}

A második egyenletnek előbb a

(- 2)

-szeresét, majd a

2

-szeresét az elsőhöz adva

\begin{matrix} a^{*} = \frac{x - 2 y + g_{7} n}{4}, b^{*} = \frac{x + 2 y + g_{8} n}{4} . \end{matrix}

(5)

Innen

a^{*}

-ra és

b^{*}

-ra mindig kapunk egész megoldást, mert

g_{7}

és

g_{8}

helyére a

0

1

2

3

értékeket téve,

n

-szeresüknek a

4

-gyel való osztás utáni maradéka valamilyen sorrendben

0

1

2

és

3

, ennélfogva bármennyi az

x - 2 y

és

x + 2 y

ugyanilyen osztásánál fellépő maradék, megválasztható

g_{7}

is,

g_{8}

is úgy, hogy

a^{*}

b^{*}

értéke egész legyen. (Valóban, ha

n = 4 k + 1

, úgy

g = 0

1

2

3

esetén

g n

maradéka rendre

0

1

2

3

, ha pedig

n = 4 k + 3

, akkor

0

3

2

1

.) Az így megválasztott

g

értékeket szükség esetén

4

-gyel növelve, csökkentve elérhetjük, hogy

a^{*}

b^{*}

-ra teljesül (1).
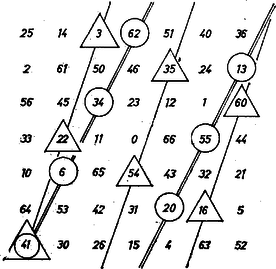
Bemutatunk egy számpéldát, ami az 1572. feladat 3. ábráját felhasználva olyan lehetőségeket is megvilágít, ha a talált

a^{*}

vagy

b^{*}

értékkel

a = c + a^{*} ≧ n

, vagy

b = d + b^{*} ≧ n

adódik.
Legyen

n = 9

x = 2

y = 7

, ekkor

g_{7}

g_{8}

helyén megfelel

4

, ill.

0

, és így

\begin{matrix} a^{*} = (2 - 14 + 4 \cdot 9) / 4 = 6, b^{*} = (2 + 14) / 4 = 4, \end{matrix}

megegyezésben a mondott ábrával. Ugyanis pl. a

\bar{c d} = \bar{04}

számnak megfelelő (

1

-gyel növelt, tízes rendszerbeli)

5

-ös számtól, a keret alatti előfordulásától jobbra

x = 2

-t, fölfelé

y = 7

-et lépve

63

-at találjuk, vagyis az

58

-cal nagyobb számot, és ez a növekedés a

9

-es számrendszerben

58 = 6 \cdot 9 + 4 = \bar{64}

, a talált

\bar{a^{*} b^{*}}

.
Az ábra több más

\bar{c d}

számához is az

58

-cal nagyobb számot találjuk, tőle jobbra

2

-t és fölfelé

7

-et, vagy ami ugyanaz, lefelé is

2

-t lépve, amíg csak a megnövelt

(c + 6) \cdot 9 + (d + 4)

szám egyik jegye sem éri el vagy lépi túl a

9

-et. Ilyen esetben viszont az

a = c + a^{*} = c + 6

, ill.

b = d + b^{*} = d + 4

számjegy helyére a

9

-cet kisebb

c - 3

, ill.

d - 5

számjegy lép, ami (4)-ből

g_{7} - 4 = 0

, ill.

g_{8} - 4 = - 4

mellett adódó

a^{*} = - 3

-nak,

b^{*} = - 5

-nek felel meg. Ezek a változások külön-külön

9 \cdot 9 = 81

, ill.

9 \cdot 1 = 9

, együtt pedig

81 + 9 = 90

csökkenést okoznak az

58

növeléssel várt értékhez képest, pl.

28

-hoz képest (aminek

27 = \bar{30}

felel meg, és itt

c + 6 = 9)

28 + 58 - 81 = 5

-öt,

6

-hoz képest

6 + 58 - 9 = 55

-öt,

33

-hoz képest

(32 = \bar{35}) 33 + 58 - 90 = 1

-et találjuk a mondott helyen.
Megegyezésben állnak ezek a tények azzal, hogy ha a feladat bélyegzőjét kiegészítenénk az

n^{2}

-nél nagyobb egész számokkal, éspedig az adott előírás szerint, pl. az

(n^{2} + 1)

-et beírnánk az

(n - 1) n + 1

-től jobbra lefelé

2

-t, ill.

1

-et lépve található mezőre, akkor

n^{2} + 1

lenyomatai átfednék az

1

-es szám lenyomatait, hiszen már magán a bélyegzőn a sorszámok különbsége a két szám oszlopaira nézve

2 n

, soraira nézve

n

lenne. Fordítva úgyis mondhatjuk ezt, hogy egy

m

szám helyén olvashatunk

m + n^{2}

-et is,

m + {g n}^{2}

-et is.

5. Az

(x, y)

pár előre közölt speciális értékeivel (5)-ből bármely páratlan

n

esetére táblázatunk eredményeit kapjuk

a^{*}

-ra és

b^{*}

-ra, vagyis arra, hogy a tetszés szerinti

\bar{c d}

számtól jobbra, ill. jobbra fölfelé, ill. balra fölfelé, ill. fölfelé álló szám első, ill. második számjegye mennyivel nagyobb, mint

c

, ill.

d

. Az első három sávban ‐ ahol

x

páratlan ‐ az eredmény más és más aszerint, hogy az

n

alakja

4 k + 1

, ill.

4 k + 3

.
A táblázat, alsó és felső sávja alapján megmutatjuk, hogy a kövezeten bárhol letéve a keretet, bármelyik sor (vagy oszlop) összege ugyanannyi. Abból adódik majd ez, ha belátjuk, hogy az egy-egy sorban, oszlopban előforduló

n

szám számjegyei között az

n

-értékű helyen is, az

1

-értékű helyen is minden fajta számjegy pontosan egyszer fordul elő, és így a

\begin{matrix} 0 + 1 + 2 + ... + (n - 2) + (n - 1) = s \end{matrix}

jelöléssel a sor összege

\begin{matrix} s \cdot n + s = s (n + 1) = \frac{(n - 1) \cdot n}{2} \cdot (n + 1) = \frac{n (n^{2} - 1)}{2}; \end{matrix}

ami pedig a kövezet összes számai összegének,

\begin{matrix} 0 + 1 + 2 + ... + (n^{2} - 2) + (n^{2} - 1) = \frac{n^{2} (n^{2} - 1)}{2} \end{matrix}

-nek

n

-edrésze.
Felhasználjuk, hogy a talált

a^{*}

b^{*}

értékek mindegyike relatív prím a megfelelő

n

-hez képest, nincs

1

-nél nagyobb közös osztójuk. Pl.

n = 4 k + 1

-nek és

a^{*} = 3 k + 1

-nek minden közös osztója egyszersmind különbségüknek,

k

-nak is osztója. Viszont

3 k + 1

-nek és

k

-nak minden közös osztója hasonlóan osztója

3 k + 1 - k - k - k = 1

-nek is, tehát nem nagyobb

1

-nél.
Legyen az

n

-edrendű kövezetből az

n \times n

mezős kerettel kijelölt négyzet egy sorában az első számnak pl. az első számjegye

c

, ekkor a sor

n

számának első számjegye rendre

\begin{matrix} c, c + a^{*}, c + 2 a^{*}, c + 3 a^{*}, ..., c + (n - 1) a^{*} \end{matrix}

(6)

(ill. ahol ez az érték nagyobb, mint

n

, ott helyette az

n

-nel való osztásánál fellépő maradék veendő). Mármost ellentmondásra jutunk annak föltevésével, hogy e számjegyek közül kettő megegyező. Ha ugyanis az

(r_{2} + 1)

-edik megegyeznék a korábbi

(r_{1} + 1)

-edikkel ‐ ahol

1 ≦ r_{1} + 1 < r_{2} + 1 ≦ n

, azaz

0 ≦ r_{1} < r_{2} ≦ n - 1 -

, vagyis

\begin{matrix} c + r_{2} a^{*} - g_{2} n = c + r_{1} a^{*} - g_{1} n \end{matrix}

volna, ebből

\begin{matrix} (r_{2} - r_{1}) a^{*} = (g_{2} - g_{1}) n = g_{3} n, \end{matrix}

következnék, vagyis hogy a bal oldal osztható

n

-nel. Ámde

a^{*}

-nak nincs közös tényezője

n

-nel, tehát

r_{2} - r_{1}

osztható vele,

\begin{matrix} r_{2} - r_{1} = g_{4} n, holott 0 < r_{2} - r_{1} < n - 1. \end{matrix}

Mindez ugyanígy érvényes a

b^{*}

értékekre.
A sor- és oszlopösszegekre vonatkozó állításunkat ezzel bebizonyítottuk. Eredményünk így is kimondható: ha a bélyegzővel készült kövezeten bárhol körülkeretezünk egy

n \times n

mezős négyzetet, majd ennek minden számából a két számjegyet két ilyen négyzet megfelelő mezőpárjaira külön-külön írjuk fel, ezek minden sorában is, minden oszlopában is a

0,1, ..., (n - 1)

számjegyek mindegyike pontosan egyszer fordul elő. Így szemléletesebb az összegek egyezésének belátása. Az ilyen elrendezéseket Euler nyomán latin négyzeteknek szokás nevezni.

6. Ha sikerülne ugyanezeket belátni az átlós irányú vonalak szám

n

-eseire ez azt bizonyítaná, hogy a bélyegzővel képezett

n

-edrendű kövezet pándiagonális, minden átlóján bűvös. Tüstént látjuk, hogy ez igaz minden olyan (páratlan)

n

-re, amely nem osztható

3

-mal. Ugyanis a táblázatunk 2. és 3.

\begin{matrix} x, y & n=4k+1 & n=4k+3 \\ a^{*} = b^{*} = 3 k + 1 & (g=3) & a^{*} = b^{*} = k + 1 & (g=1) \\ (1; 0) \\ jobb & = \frac{3 n + 1}{4} & = \frac{n + 1}{4} \\ szomszéd \\ mindkét esetbena^{*} - b^{*} = 0 \\ (1; 1) & a^{*} = k = \frac{n - 1}{4}, & b^{*} = k + 1 = \frac{n + 3}{4} & a^{*} = 3 k + 2, & b^{*} = 3 k + 3 \\ jobb & (relatív prím) & = \frac{3 n - 1}{4}, & = \frac{3 n + 3}{4} \\ felső \\ (rel.pr.) \\ (-1; 1) & a^{*} = 3 k & b^{*} = 3 k + 1 & a^{*} = k & b^{*} = k + 1 \\ bal & = \frac{3 n - 3}{4} & = \frac{3 n + 1}{4} & = \frac{n - 3}{4} & = \frac{n + 1}{4} \\ felső \\ (rel. pr) & (rel. pr.) \\ (0; 1) & nalakjától függetlenül (vagyisn = 2 k + 1-re) \\ felső & a^{*} = k = \frac{n - 1}{2}, & b^{*} = k + 1 = \frac{n + 1}{2}, & a^{*} + b^{*} = n \end{matrix}

sávjában talált

a^{*}

b^{*}

értékek közül

n = 4 k + 1

oszlopában

a^{*} = k

és

b^{*} = 3 k + 1

valamint

n = 4 k + 3

oszlopában

a^{*} = 3 k + 2

és

b^{*} = k + 1

a fentiekhez hasonlóan mindenesetre relatív prímek

n

-hez. A további négy értéknek pedig nem lehet más közös osztója a megfelelői

n

-nel, mint a

3

-as szám, hiszen pl.

b^{*} = k + 1

esetében (az

(1; 1)

sávban)

\begin{matrix} 4 k + 1 - (k + 1) = 3 k, \end{matrix}

és itt a

k

tényező relatív prím

4 k + 1

-hez, tehát a mondott

n

-ekre

3 k

is,

k + 1

is relatív prím hozzá. Ugyanezek állnak

n = 4 k + 1

oszlopában

a^{*} = 3 k

-ra és

n = 4 k + 3

oszlopában

b^{*} = 3 k + 3

-ra,

a^{*} = k

-ra. A tekintetbe vett

n

-ekre tehát a jegyek szétválasztásával képezett két négyzet átlós latin négyzet, átlós összegei is egyezők, a keret bárhol való elhelyezése esetében. Ezt láttuk az 1572. feladatban

n = 5

és

7

esetében.
Ha viszont

n = 3 g

, akkor az utoljára vizsgált négy

a^{*}

b^{*}

kifejezés osztható

3

-mal, (6)-nak már a

(g + 1)

-edik tagja egyezik az elsővel,

c

-vel, mert (

a^{*} = 3 a^{* *}

jelöléssel)

\begin{matrix} c + g a^{*} = c + 3 g a^{* *}, \end{matrix}

és tovább tagról-tagra ismétlődik a megegyezés. A kettéválasztott számjegyek négyzeteinek tehát ilyenkor nincs meg mindkét átlós irányban a ,,latin'' tulajdonsága (az egyik irányban azonban megvan). Meg lehet mutatni, hogy ilyenkor mindkét irányban minden harmadik átlóban megfelelő az összeg, a közbülsőkben viszont attól eltér, ezt láttuk az 1572. feladatban

n = 9

esetében.

n = 3

mellett pedig az adódik, hogy a lényegében egyetlen

3

-adrendű bűvös kövezet nem pándiagonális. Ezzel a bélyegzőnkkel készített kövezetek pándiagonálisságának kérdését megválaszoltuk.

Megjegyezzük, hogy legutóbbi megállapításunk korántsem jelenti azt, hogy

3

-mal osztható rendszám esetén nem létezik pándiagonális kövezet. Az idézett 3. ábrából

(n = 9)

pándiagonális bűvös négyzet ‐ tehát kövezet is ‐ képezhető a következő változtatásokkal: számait rendre

1

-gyel csökkentjük és átírjuk a

9

alapú számrendszerbe, ezután a számjegyekben három alkalmas cserét hajtunk végre, pl. minden

\begin{matrix} 0, 1; 3, 5 7, 8 \end{matrix}

számjegy helyére a

9

-es és

1

-es értékű helyen egyaránt a következőt írjuk:

\begin{matrix} 1, 0; 5, 3; 8, 7. \end{matrix}

A számok növekvő rendjét tekintve ez már nem kétféle lépéssel, pecsételéssel képezett alakzat. Ebből is látható, hogy vannak más típusú bűvös négyzetek is. Már az

5

-ödrendűekre vonatkozóan sem ismeretes ez ideig az összes bűvös négyzetek száma.

7. Az olvasóra hagyjuk annak átgondolását, hogy bélyegzőnk ,,jobbra

2

-t és fölfelé vagy lefelé

1

-et'' lépései azért vezethettek minden páratlan

n

esetén soraikban és oszlopaikban latin négyzetekre bontható négyzetekhez ‐ és az ezekből folyó eredményekhez, ‐, mert a lépések

2

-es, ill.

1

-es komponense minden páratlan

n

-hez képest relatív prím. Megfelelne helyettük lépéskomponensként minden páratlan

n

esetére bármely

2^{e}

mezőnyi eltolódás (vízszintesen is, függőlegesen is), ahol

e ≧ 0

, egész szám ‐ azonban természetesen a bélyegző

1

-eséről a

2

-esre és az

n + 1

-esre vivő lépésnek és a komponensek arányának is különbözőnek kell lennie.
8. Az elmondottak gyakorlásául ajánljuk annak vizsgálatát, hogy az így előállított kövezeteken a figyelembe vett

x i + y j

vektoroktól különböző lépéseket

n

-szer ismételve, találhatunk-e más, a bűvös állandóval egyező összegeket. Indításul bemutatjuk az

n = 7

-re és a

7

-es számrendszerben készült ábrát, melyen

\bar{00}

-tól a

\bar{01}

szám

2 i + j

-re, az

\bar{10}

pedig

4 i - j

-re áll (meg lehet mutatni a fenti eljárással a kövezet felírása nélkül előre is, hogy pándiagonális lesz), és pl. a kis körökbe foglalt

(i + 2 j

lépéssel kapott) számok összege is, a kis háromszögbe foglaltak is egyenlő a bűvös állandóval, mert két összekötött szám jegyei mind a

7

-es, mind az

1

-es helyen különbözők.

Ebben azonban az is lényeges, hogy itt

n

-ként prímszámot vettünk. A megjelölt számhetesek persze sok más ,,nagyobb'' lépéssel is összejönnek, pl. a háromszögbe foglaltak

2 i - j

-vel,

3 i + 2 j

-vel,

2 i + 6 j

-vel s i. t.

^{$^{*}$}Lásd ezen számban, 103. o.