Kezdőlap


Cím:	Pályázat az inverzióról
Szerző(k):	Bártfai Pál , Tusnády Gábor
Füzet:	1971/január, 1 - 7. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbiakban az inverzióra vonatkozó feladatokat közlünk. E feladatok megoldását bárki beküldheti a szokásos módon: minden feladat megoldását külön lapon kérjük, beküldési határidő 1971. április 25. Kérjük a versenyzőinket, hogy pályázatunkra küldött megoldásaikat külön borítékba tegyék, a borítékra írják rá, hogy "Pályázat az inverzióról''. A közölt feladatok alkalmazását három példán mutatjuk be. Az inverzióra vonatkozó szükséges ismeretek megtalálhatók például a K. M. L. 37. kötet 97‐101. oldalán (1968. november). Megemlítjük továbbá, hogy az inverzióval kapcsolatos a pontversenyen kívül közölt 12., 28., 31. és 44. probléma.

1. feladat. Legyen az inverzió alapkörének középpontja

O

, sugara

r

, a sík két tetszőleges,

O

-tól különböző pontja

Q

és

S

, ezek inverze

Q'

és

S'

. Bizonyítandó, hogy

\begin{matrix} \frac{Q' S'}{Q S} = \frac{O S'}{O Q} = \frac{O Q'}{O S} . \end{matrix}

I. példa (Apollóniosz kör). Adott a síkban két különböző pont,

A

és

B

, továbbá egy pozitív valós szám

λ (λ \neq 1)

. Azoknak a pontoknak a mértani helye a síkban, melyek

A

-tól

λ

-szor akkora távolságra vannak, mint

B

-től, egy kör, melyre

A

-t invertálva

B

-t kapjuk.
Állításunkat a

λ = 1

esetre vezetjük vissza az inverzió segítségével. Legyen egyelőre az inverzió alapköre tetszőleges (középpontja

O

, sugara

r

), az adott

A

B

pontok és a tetszőleges

P

pont inverze

A'

B'

P'

. (Feltesszük, hogy

A

B

P

és

O

különbözőek.) Az 1. feladat alapján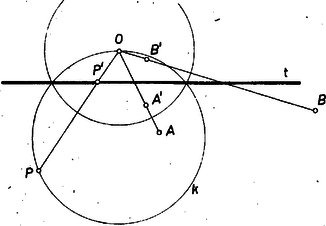

\begin{matrix} \frac{A' P'}{A P} = \frac{O P'}{O A}, \frac{B' P'}{B P} = \frac{O P'}{O B}, \end{matrix}

tehát

\begin{matrix} \frac{A' P'}{B' P'} : \frac{A P}{B P} = \frac{O B}{O A} . \end{matrix}

Válasszuk

O

-t úgy, hogy a vizsgált mértani helyhez tartozzék, vagyis

O A = λ O B

legyen. (Könnyen látható, hogy van ilyen pont; 1. ábra)

1. ábra

Ekkor

\begin{matrix} \frac{A' P'}{B' P'} = \frac{O B}{O A} \cdot \frac{A P}{B P} = \frac{1}{λ} \cdot \frac{A P}{B P}, \end{matrix}

így

P

akkor és csakis akkor lesz a vizsgált mértani hely

O

-tól különböző pontja, ha

A' P' = B' P'

, vagyis

P'

A' B'

szakasz

t

felező merőlegesén van.

t

nem mehet át

O

-n, hiszen ekkor

O A' = O B'

volna, és ebből

O A = O B

következne, ami

O A = λ O B

és

λ \neq 1

miatt nem lehet. Eszerint a vizsgált mértani helyhez

O

-n kívül

t

pontjainak inverzei tartoznak. Ezek az inverz pontok egy

O

-n átmenő

k

kör

O

-tól különböző pontjai. A vizsgált mértani hely tehát a

k

kör.
A pontversenyen kívül közölt 31. probléma szerint, ha adott egy kör (vagy egyenes) és két pont, melyek az adott körre (vagy egyenesre) nézve inverz (vagy tükrös) párok, és az egész alakzatot egy tetszőleges alapkörre invertáljuk, az adott pontok olyan pontokba mennek át, melyek az adott kör (vagy egyenes) inverzére nézve (ami ismét kör vagy egyenes) inverz vagy tükrös párt alkotnak.
Eszerint abból, hogy az

A'

B'

pontok a

t

tengelyre nézve tükrös párt alkotnak, következik, hogy

A

és

B

k

-ra nézve inverz pontpár, állításunkat ezzel bebizonyítottuk.

2. feladat. Adott a síkban 3 különböző pont:

A

B

C

. Szerkesszük meg azt a kört, amelyik átmegy

C

-n és amelyikre

A

-t invertálva

B

-t kapjuk.

3. feladat. Adott a síkban 3 különböző pont:

A

B

C

. Legyen

k_{a}

A

-n átmenő,

B

-t

C

-be vivő,

k_{b}

B

-n átmenő,

C

-t

A

-ba vivő,

k_{c}

, a

C

-n átmenő,

A

-t

B

-be vivő inverzió alapköre. Mutassuk meg, hogy van két pont, amelyeken e három kör mindegyike átmegy.

4. feladat. Adott a síkban 3 különböző pont:

A

B

C

. Jellemezzük azokat a köröket, melyekre invertálva az adott pontokat, a kapott

A'

B'

C'

pontokra

A' C' = B' C'

teljesül.

5. feladat. Adott egy tetszőleges háromszög. Van-e olyan inverzió, mely a háromszög csúcsaihoz egy szabályos háromszög csúcsait rendeli hozzá?

II. példa. Legyenek az

A B C

háromszög oldalai különbözőek, a háromszög belső, ill. külső szögfelezői messék a szemközti oldalt az

A_{1}

B_{1}

C_{1}

, ill.

A_{2}

B_{2}

C_{2}

pontokban, az

A_{1} A_{2}

B_{1} B_{2}

C_{1} C_{2}

szakaszok fölé rajzolt Thalész körök legyenek rendre

k_{a}

k_{b}

k_{c}

. Megmutatjuk, hogy van két pont,

M_{1}

és

M_{2}

, melyeken e három kör mindegyike átmegy, és e körök

60^{\circ}

-os szögben metszik egymást (2. ábra).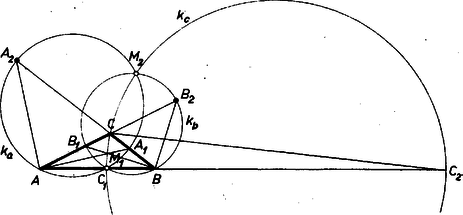

2. ábra

A feladatban szereplő pontokat a háromszög Miguel pontjainak nevezzük. Könnyen látható, hogy ha egyenlő szárú háromszögben a megfelelő kört oldalfelező merőlegessel helyettesítjük, feladatunk állítása érvényben marad, szabályos háromszögnek azonban csak egy ilyen pontja van. Állításunk egy részét tartalmazta az 1686. feladat.^{$^{*}$}
Ismeretes, hogy a háromszög szögfelezői olyan arányban osztják a szemközti oldalt, mint a szög szárain levő oldalak aránya, így

\begin{matrix} A C_{1} : B C_{1} = A C_{2} : B C_{2} = A C : B C . \end{matrix}

C_{1}

C_{2}

C

pontok tehát rajta vannak az

A

B

pontokhoz és

λ = \frac{b}{a}

számhoz tartozó Apolloniosz-körön (I. példa), ez az Apolloniosz kör tehát azonos

k_{c}

-vel és

A

-t

k_{c}

-re invertálva

B

-t kapjuk. Hasonló állítás mondható ki a

k_{b}

k_{a}

körökre is. Így

M_{1}

M_{2}

létezését a 3. feladat állítása biztosítja.
Mivel

A

-t

k_{b}

-re invertálva

C

-be megy át, az

M_{1} M_{2}

pontok pedig helyükön maradnak, az

A

M_{1}

M_{2}

pontokon átmenő

k_{a}

körnek

k_{b}

-re vonatkozó inverze a

C

M_{1}

M_{2}

pontokon átmenő

k_{c}

kör. Tudjuk, hogy az inverzió szögtartó, tehát

k_{a}

és

k_{c}

, a

k_{b}

-vel ugyanakkora szöget zárnak be, ami azt jelenti, hogy az

M_{1}

-en átmenő

k_{a}

k_{b}

k_{c}

köröket érintő

e

f

g

egyenesek közül az

e

és

g

f

-fel egyenlő szögeket zárnak be. (Mivel a körök metszik egymást

M_{1}

-ben, ezek az egyenesek különbözők.) Hasonló módon láthatjuk be, hogy

g

-vel az

e

és

f

egyenesek egyenlő szögeket zárnak be, tehát e három egyenes 6 egyenlő szöget határoz meg és e szögek

60^{\circ}

-osak.
Állításunkat másképp is bebizonyíthatjuk: legyen

k

tetszőleges

M_{1}

középpontú kör.

k

-ra invertálva a

k_{a}

k_{b}

k_{c}

, köröket egyeneseket kapunk, jelöljük ezeket

k'_{a}

k'_{b}

k'_{c}

-ve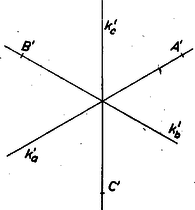l (3. ábra).

3. ábra

Ezek az egyenesek egy ponton mennek át,

M_{2}

inverzén. Jelöljük

A

B

C

inverzét

A'

B'

C'

-vel: ezek rendre a

k'_{a}

k'_{b}

k'_{c}

, egyeneseken vannak. A 31. probléma már idézett állítása szerint abból, hogy

A

k_{b}

-re vonatkozó inverze

C

, következik, hogy

A'

és

C'

k'_{b}

-re tükrősen helyezkednek el, tehát

A' B' = B' C'

. Hasonlóan kapjuk, hogy

A' B' = C' A'

, tehát

A' B' C'

szabályosan háromszög, a

k'_{a}

k'_{b}

k'_{c}

egyenesek közti szögek

60^{\circ}

-osak és mivel az inverzió szögtartó, ugyanekkorák a

k_{a}

k_{b}

k_{c}

körök közti szögek is.

6. feladat. Adott a síkban két kör,

k_{1}

és

k_{2}

, melyek nem metszik egymást és egyik sincs a másik belsejében. Mutassuk meg, hogy két olyan pont van a síkban, melyek körül tetszőleges

k

kört rajzolva, a

k_{1}

k_{2}

körök

k

-ra vonatkozó

k'_{1}

k'_{2}

inverzei koncentrikus körök.

7. feladat. Adott a síkban két kör, melyeknek van közös belső érintőjük. Mutassuk meg, hogy van két pont a síkban, melyeken e körök tetszőleges közös (külső vagy belső) érintőjének az érintési pontok közti szakasza fölé rajzolt Thalesz kör átmegy.

8. feladat. Legyen

k_{1}

A B C

háromszögbe írt kör, melynek középpontja

O_{1}

, és érintse

k_{1}

az oldalakat rendre az

A_{1}

B_{1}

C_{1}

pontokban. Mutassuk meg, hogy
a) az

A

B

C

pontok

k_{1}

-re vonatkozó

A'

B'

C'

inverzei rendre felezik a

B_{1} C_{1}

C_{1} A_{1}

A_{1} B_{1}

szakaszokat,

b) az

A B C

háromszög oldalegyeneseinek

k_{1}

-re vonatkozó inverzei az

A_{1} O_{1}

B_{1} O_{1}

C_{1} O_{1}

szakaszok feletti Thalesz körök,

c) az

A B C

háromszög köré írható

k

kör inverze az

A_{1} B_{1} C_{1}

háromszög Feuerbach köre.

9. feladat. Bizonyítsuk be Euler következő tételét: két adott körhöz (

k

-hoz és

k_{1}

-hez) akkor és csakis akkor van olyan háromszög, melynek

k

a körülírt,

k_{1}

a beírt köre, ha

\begin{matrix} d^{2} + r_{1}^{2} = {(r - r_{1})}^{2}, \end{matrix}

ahol

r

r_{1}

k

k_{1}

sugara,

d

a középpontok távolsága.

III. példa (az 1969. évi Nemzetközi Matematikai Diákolimpia 4. feladatának¹ általánosítása). Legyen az

A B C

háromszög körülírt köre

k

, beírt köre

k_{1}

, az

A B

szakasz tetszőleges belső pontja

D

. Jelöljük az

A B

egyenest

c

-vel, a

D C

félegyenest

d

-vel. A

c

egyenest, a

k

kört és a

d

félegyenest érintő két kör legyen

k_{2}

és

k_{3}

(4. 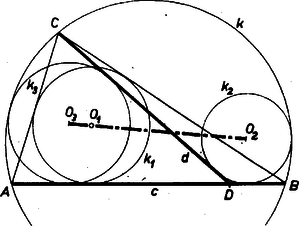ábra).

4. ábra

Megmutatjuk, hogy

a) a

k_{1}

k_{2}

k_{3}

kör

O_{1}

O_{2}

O_{3}

középpontja egy egyenesen van,

b) a

k_{1}

kört a

k_{2}

k_{3}

körök és a

d

félegyenes egyértelműen meghatározzák.
Állításunk b) része részletesebben a következőt jelenti. Legyen

k_{2}

és

k_{3}

két egymást nem metsző kör, középpontjuk

O_{2}

O_{3}

, közös külső érintőjük

c

és

c_{1}

. E körök egyik közös belső érintője messe

c

-t

D

-ben és legyen

d

ennek a belső érintőnek az a

D

-ből kiinduló félegyenese, amelyik

c

-nek ugyanazon az oldalán van, mint a

k_{2}

k_{3}

kör. Legyen továbbá

d

és

c_{1}

metszéspontjának,

P

-nek a vetülete az

O_{2} O_{3}

centrálison,

O_{1}

, és legyen

k_{1}

, az

O_{1}

körül írt,

c

-t érintő kör. Ekkor

k_{1}

beírt köre lesz minden olyan háromszögnek, melynek csúcsait a

c

egyenesből és a

d

félegyenesből egy, a

k_{2}

k_{3}

köröket kívülről érintő

k

kör metszi ki.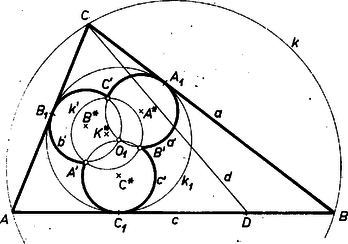

5. ábra

Állításunk a) részének a bizonyítása a következő. Jelöljük az

A B C

háromszög másik két oldalát

a

-val,

b

-vel, érintse

k_{1}

az oldalakat az

A_{1}

B_{1}

C_{1}

pontokban (5. ábra). A 8. feladat szerint a

k_{1}

körre invertálva az

A B C

háromszög csúcsai az

A_{1} B_{1} C_{1}

háromszög

A' B' C'

középháromszögének a csúcsaiba mennek át. Az

a

b

c

oldalak

a'

b'

c'

inverze pedig az

A_{1} O_{1}

B_{1} O_{1}

C_{1} O_{1}

szakaszok feletti Thalesz kör, jelöljük ezek középpontját rendre

A^{*}

-gal,

B^{*}

-gal,

C^{*}

-gal. Továbbá az

A B C

háromszög köré írt

k

kör

k_{1}

-re vonatkozó

k'

inverze pedig az

A' B' C'

háromszög köré írható kör lesz, jelöljük ennek középpontját

K^{*}

-gal. Legyen

d_{1}

k_{2}

k_{3}

vonal

k_{1}

-re vonatkozó inverze

d'

k'_{2}

k'_{3}

, középpontjuk

D^{*}

K_{2}^{*}

K_{3}^{*}

. Azt fogjuk megmutatni, hogy

K_{2}^{*}

és

K_{3}^{*}

azonosak: ebből következik a bizonyítandó állítás, hiszen ekkor az

O_{1}

K_{2}^{*}

K_{3}^{*}

pontok nyilvánvalóan egy egyenesen vannak, tehát egy egyenesen vannak az

O_{1}

O_{2}

O_{3}

pontok is.
Az

a'

b'

körök a

C'

O_{1}

pontokban metszik egymást, így az

O_{1} A^{*} C' B^{*}

négyszög rombusz (6. ábra).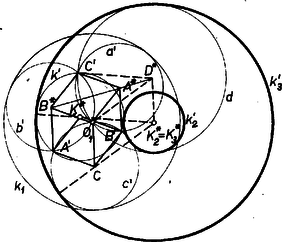

6. ábra

Hasonlóan látható be, hogy

O_{1} B^{*} A' C^{*}

és

O_{1} C^{*} B' A^{*}

is rombusz. Az

a'

k'

körök egymást a

B'

C'

pontokban metszik, így az

A^{*} B' K^{*} C'

négyszög rombusz, és hasonlóan látható be, hogy

B^{*} C' K^{*} A'

és

C^{*} A' K^{*} B'

is rombusz.
A

k_{1}

-re való invertálás az

a

b

egyeneseknek a

k_{1}

-et nem tartalmazó oldalán levő pontokat viszi az

a'

;

b'

körök belsejébe. Mivel

D

A B

szakaszon van,

k_{1}

-re vonatkozó

D'

inverze az

a'

b'

körökön kívül van. Emiatt a

d'

kör nem lehet teljes egészében az

a'

b'

körök által lefedett síkrészben, vagyis

D^{*}

nem lehet az

A^{*} B^{*}

szakaszon, tehát a

d'

kör

R

sugara nagyobb az

a'

b'

c'

k'

körök

r

sugaránál (ezek a körök egyenlő sugarúak, hiszen mindegyiknek az átmérője egyenlő

k_{1}

sugarával).

k_{1}

-re való invertálás a

k

körön kívül levő pontokat, illetve a

c

egyenes

O_{1}

-et nem tartalmazó oldalán levő pontokat a

k'

, illetve a

c'

kör belsejébe viszi, emiatt a

k'_{2}

k'_{3}

körök a

k'

c'

köröket kívülről érintik. Közülük az egyik belülről, a másik kívülről érinti

d'

-t, legyen az első a

k'_{2}

a második a

k'_{3}

. (Felhasználjuk, hogy adott három kört adott módon érintő kör egyértelműen van meghatározva, ha egyáltalán létezik.) Láttuk, hogy van olyan eltolás, amely az

A^{*} C' B^{*} O_{1}

rombuszt a

B' K^{*} A' C^{*}

rombuszba viszi (hiszen a megfelelő csúcsokat összekötő szakaszok párhuzamosak, és egyenlőek

r

-rel), vigye ez az eltolás a

D

pontot egy

X

pontba.

X

körül (

R - r

) sugárral kört rajzolva a

d'

kört belülről érintő kört kapjuk, hiszen e két kör középpontjainak a távolsága egyenlő sugaraik különbségével,

r

-rel. Ez a kör kívülről érinti a

c'

k'

köröket, hiszen középpontjaik távolsága egyenlő sugaraik összegével,

R

-rel. Ez a kör tehát a

k'_{2}

, így

X \equiv K_{2}^{*}

. Hasonlóan látható be, hogy az

X

körül (

R + r

) sugárral írt kört a

c'

k'

d'

körök belülről érintik, tehát ez a kör a

k'_{3}

, és így

X \equiv K_{3}^{*}

, vagyis

K_{2}^{*} \equiv K_{3}^{*}

, amint azt bizonyítanunk kellett.

Állításunk b) részének a bizonyítása a következő. Legyen

k_{2}

k_{3}

c

d

adott, az

A B C

háromszöget határozza meg egy tetszőleges

k

kör és legyen egyelőre

k_{1}

A B C

háromszög beírt köre. Megmutatjuk, hogy

k_{1}

az általunk meghatározott módon is megszerkeszthető. Ismét a

k_{1}

körre invertáljuk az alakzatot, felhasználjuk azokat az eredményeket, amelyeket az a) rész bizonyításánál kaptunk, és tovább használjuk ottani jelöléseinket.
Tükrözzük a

c'

kört az

O_{1}

K_{2}^{*}

pontok által meghatározott

t

tengelyre, a kapott kör legyen

c'_{1}

, középpontja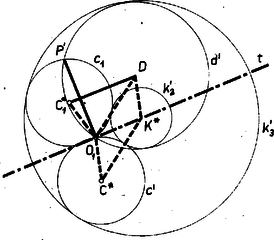

C_{1}^{*}

(7. ábra).

7. ábra

c'_{1}

inverze

k_{2}

és

k_{3}

másik közös külső érintője, tehát

c'_{1}

inverze a

c_{1}

egyenes. Az

O_{1} D^{*} K_{2}^{*} C^{*}

négyszög paralelogramma, melynek centrálszimmetriájáhól következik, hogy

D^{*}

és

C^{*}

egyenlő távolságra van

t

-től, a tükrözés folytán ugyanez igaz

D^{*}

-ra és

C_{1}^{*}

-ra, de ez a két pont már

t

-nek ugyanazon az oldalán van.

D^{*}

és

C_{1}^{*}

nem eshetnek egybe, mert akkor a

d'

és

c'_{1}

körök, illetve a

d

és

c_{1}

egyenesek egybeesnének, ami lehetetlen, hiszen egyikük belső, másikuk külső érintője a

k_{2}

k_{3}

köröknek. A

C_{1}^{*} D^{*}

szakasz tehát párhuzamos

t

-vel, és így a

c'_{1}

d'

körök

O_{1}

-en kívüli

P'

közös pontja

O_{1}

-gyel együtt

t

-re merőleges egyenest határoz meg.

P'

azonban

c_{1}

és

d

metszéspontjának,

P

-nek inverze, tehát

O_{1}

-et megkaphatjuk a

P

-nek

O_{2} O_{3}

-ra történő merőleges vetítésével. Ezzel

k_{1}

középpontját a

k

kör helyzetétől függetlenül meghatároztuk, sugarát pedig meghatározza az a tény, hogy ez a kör érinti

c

-t.

10. feladat. A 3. példához kapcsolódva mutassuk meg, hogy ha

d

merőleges

c

-re, akkor

O_{1}

felezi az

O_{2} O_{3}

szakaszt.

^{$^{*}$}Lásd K. M. L. 41 (1970) 113. o.

¹Lásd K. M. L. 1680. feladat, 40 (1970) 152. o.