Kezdőlap


Cím:	Az 1970. évi fizika OKTV feladatai
Füzet:	1970/október, 81 - 88. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Függőlegesen felfelé lőtt lövedék a legnagyobb magasság elérésekor $m_{1} = 3 kg$ és $m_{2} = 6 kg$ tömegű részekre robbant szét. A két rész a fellövés helyétől egyenlő távolságokban $T = 4$ másodperces időkülönbséggel ért talajt. Mekkora magasságban robbant szét a lövedék? (A levegő közegellenállását ne vegyük figyelembe.)

(Párkányi László)

Megoldás. A robbanás pillanatában a lövedék nyugalomban volt és részei ellentétes irányokban,

α

szögben repültek szét

v_{1}

és

v_{2}

kezdősebességekkel (1. ábra).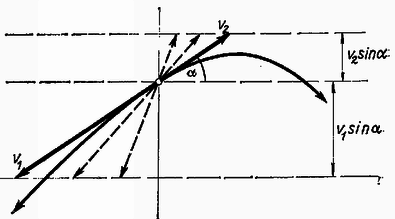

1. ábra

Az impulzustörvény értelmében

m_{1} v_{1} = m_{2} v_{2}

. Jelöljük a tömegek arányát

k

-val, akkor a sebességek aránya

1 / k :

\begin{matrix} k = \frac{m_{2}}{m_{1}} = \frac{v_{1}}{v_{2}} . \end{matrix}

A robbanástól a földetérésig

t_{1}

, ill.

t_{2}

idő telt el. A távolságok egyenlőségéből:

\begin{matrix} v_{1} cos α \cdot t_{1} = v_{2} cos α \cdot t_{2} . \end{matrix}

Tehát az idők hányadosát ugyanaz a

k

adja meg:

\begin{matrix} k = \frac{t_{2}}{t_{1}} . \end{matrix}

(1)

Másrészt tudjuk, hogy az időkülönbség:

\begin{matrix} t_{2} - t_{1} = T . \end{matrix}

(2)

Az (1) és (2)-ből álló egyenletrendszer megoldása adja az időtartamokat:

\begin{matrix} t_{1} = \frac{T}{k - 1}, t_{2} = \frac{k T}{k - 1} . \end{matrix}

(3)

A robbanás helyének

h

magassága, (1) felhasználásával:

\begin{matrix} h = v_{1} sin α \cdot t_{1} + \frac{g}{2} \cdot t_{1}^{2} = k v_{2} sin α \cdot t_{1} + \frac{g}{2} \cdot t_{1}^{2}, h = - v_{2} sin α \cdot t_{2} + \frac{g}{2} \cdot t_{2}^{2} . \end{matrix}

Ez a két egyenlet egyenletrendszer

h

és

v_{2} sin α

számára. A (3) alatti értékek felhasználásával a megoldások:

\begin{matrix} h = \frac{g}{4} \cdot \frac{k^{2} + 1}{{(k - 1)}^{2}} \cdot T^{2}, v_{2} sin α = \frac{g (k + 1)}{4 k} \cdot T . \end{matrix}

Mivel

t_{2} / t_{1} = m_{2} / m_{1}

, azért

m_{2} > m_{1}

esetén

t_{2} > t_{1}

tehát ekkor a nagyobb

m_{2}

tömegnek kell felfelé indulnia. A feladat adataiból

v_{1}

és

v_{2}

nem számítható ki, csak

v_{1}

sin

α

és

v_{2} sin α

. A lehetséges

v_{1}

és

v_{2}

sebességvektorok végpontjai párhuzamos egyeneseken vannak (1. ábra).
Feladatunk számadataival

k = 2

t_{1} = 4 s

t_{2} = 8 s

h = 196 méter

v_{2} sin α = 14, 7 m/s

v_{1} sin α = 29, 4 m/s

2. Vízszintes,

l

szélességű asztallapon átvetünk egy

L

hosszúságú, súlyos, tökéletesen hajlékony kötelet. Kezdetben a két lelógó kötélvég egyenlő hosszú. Az egyik kötélvéget kissé meghúzva a kötél mozgásnak indul. Vizsgáljuk meg a kötélben ható feszítőerőt a kötél egyes helyein, mozgás közben ! (A súrlódástól tekintsünk el.) Legyen

L = 100 cm

l = 20 cm

(Wiedemann László)

Megoldás. Kezdetben az asztal mindkét oldalán

(L - l) / 2

hosszúságú kötél lóg le (2. ábra).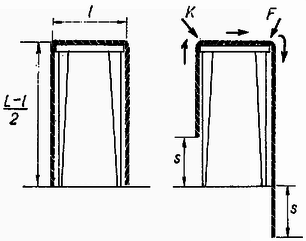

2. ábra

A mozgásban levő kötél helyzetét végének

s

útjával jelöljük meg. A gyorsuló kötél mentén a fonálerő lineárisan változik, hiszen mindegyik keresztmetszetben működő erőnek a mögötte levő kötél tömegét kell gyorsítania. Az asztal élein a fonálerők

K

és

F

, a szabad végeken nulla. Célunk

K

és

F

meghatározása

s

függvényében.
Jelentse

σ

az 1 méter hosszú kötél tömegét és

a

a gyorsulást.

F

-nél a lelógó kötél tömege

[(L - l) / 2 + s] σ

, az

F

fonálerő a súly és gyorsító erő különbsége:

\begin{matrix} F = σ [\frac{L - l}{2} + s] g - σ [\frac{L - l}{2} + s] a . \end{matrix}

A másik élnél lelógó kötél tömege

[(L - l) / 2 - s] σ

, a

K

fonálerő a súly és gyorsító erő összege:

\begin{matrix} K = σ [\frac{L - l}{2} - s] g + σ [\frac{L - l}{2} - s] a . \end{matrix}

Az asztalon fekvő kötéldarabot gyorsító erő:

\begin{matrix} F - K = σ l a . \end{matrix}

Ez a három egyenlet egy egyenletrendszert alkot, amelynek megoldása:

\begin{matrix} a = \frac{2 g}{L} \cdot s, \\ F = - \frac{2 g σ}{L} \cdot s^{2} + \frac{g σ l}{L} \cdot s + \frac{g σ (L - l)}{2}, \end{matrix}

\begin{matrix} K = - \frac{2 g σ}{L} \cdot s^{2} - \frac{g σ l}{L} \cdot s + \frac{g σ (L - l)}{2} . \end{matrix}

Ezek a képletek csak addig érvényesek, ameddig

K

-nál is van még lelógó kötélvég. Ezután új számítást kell végezni. A lelógó kötélvég súlya gyorsítja az egész kötél tömegét:

\begin{matrix} σ [\frac{L - l}{2} + s] g = σ L a; \end{matrix}

K

-ban működő fonálerő számára megmarad az előbbi egyenlet. Most az egyenletrendszer megoldása:

\begin{matrix} a = g \cdot [\frac{s}{L} + \frac{L - l}{2 L}], \\ F = - \frac{g σ}{L} \cdot s^{2} + \frac{g σ l}{L} \cdot s + \frac{g σ (L^{2} - l^{2})}{4 L} . \end{matrix}

A fonálerők alakulását a 3. ábra mutatja.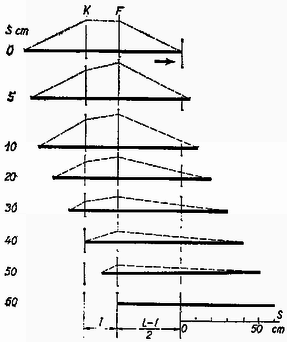

3. ábra

Az egymás alatti rajzokon a kötél helyzete látszik csúszás közben, a lelógó részeket is vízszintesen rajzolva. A szaggatott vonal mutatja az illető helyen, a kötél azon helyzetében a fonálerő nagyságát. A gyorsulást és az asztal szélein jelentkező

F

és

K

kötélerőket a megtett út függvényében mutatja a 4. ábra.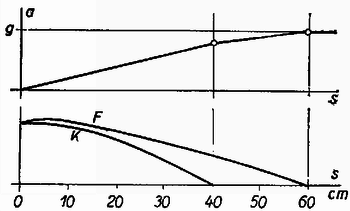

4. ábra

F

erőnek maximuma van akkor, amikor a megtett út

l / 4

. Számításainkban a gyorsulást és az erőket az út függvényében számítottuk, az időtől való függés megvizsgálása nehezebb feladat.

3. Igen nagy alapterületű medencében vízre

0, 8 {p / c m}^{3}

fajsúlyú olajat rétegeztünk nagy vastagságban. Egy

2 dm

élhosszúságú,

1, 7 {p / c m}^{3}

fajsúlyú magnéziumkocka úgy lóg egy fonálon, hogy felső lapja

0, 5 dm

-re van a határfelület alatt. A kockát felhúzzuk úgy, hogy alsó lapja

0, 5 dm

-re legyen a határfelület felett. Mennyi munkát végeztünk ?

Megoldás. A kocka térfogata

2^{3} = 8 {d m}^{3}

, súlya

1, 7 \cdot 8 kp=1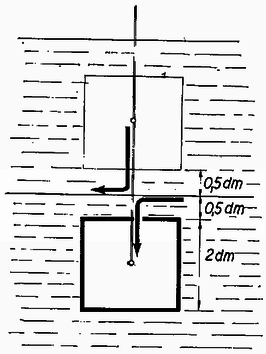3,6 kp

5. ábra

A kocka súlypontja

3 dm= 0,3 m

távolsággal kerül feljebb (5. ábra), ezért a kocka felhúzásához

0, 3 \cdot 13, 6 mkp=4,08 mkp

munkavégzés kellene. Azonban közben a kocka elhagyott helyére a határfelületről

8 kp

súlyú víz folyik le, a súlypontig számítva

1, 5 dm= 0,15 m

szintkülönbségen át. Innen

0, 15 \cdot 8 mkp=1,2 mkp

munkát kapunk. A kocka új helyéről a határfelületre

0, 8 \cdot 8 kp=6,4 kp

súlyú olaj folyik le,

0, 15 m

szintkülönbségen át. Ebből

0, 15 \cdot 6, 4 mkp=0,96 mkp

munkát kapunk. Összesítve a kocka felhúzásához

(4, 08 - 1, 2 - 0, 96 mkp) = 1, 92 mkp

munkavégzés szükséges.
Ez a számítás és ez az eredmény csak akkor érvényes, ha a medence alapterülete igen nagy. Különben megváltozik felhúzás közben a két folyadék határfelületének magassága.

A II. forduló feladatai

R = 8, 16

méter sugarú, függőleges körpálya legmélyebb pontjáról

v_{0} = 20 m/s

kezdősebességgel indítunk el egy kis tárgyat és ez a kör belsejében körülfut. A körpálya milyen nagy része hiányozhat, ha azt akarjuk, hogy a mutatvány mégis sikerüljön ? (A súrlódást ne vegyük figyelembe.

g = 9, 8 {m / s}^{2})

(Bártfai Tamás)

Megoldás. A tárgy helyzetét határozza meg

α

szög (6. ábra).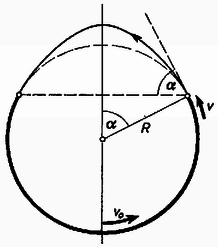

6. ábra

Az alsó indítási sebesség legyen mint

\sqrt[]{g R}

többszöröse megadva:

v_{0}^{2} = k \cdot g R

. Az

α

szöggel meghatározott helyzetben meglevő

v

sebességet az energiamegmaradás törvényével számítjuk:

\begin{matrix} v^{2} = v_{0}^{2} - 2 g R (1 + cos α); \end{matrix}

itt

v_{0}^{2}

k

-val kifejezett értékét használva:

\begin{matrix} v^{2} = [(k - 2) - 2 cos α] \cdot g R . \end{matrix}

(4)

Ha a fal megszűnik, ferde hajítás kezdődik

α

szög alatt, ezzel a kezdősebességgel. A fal elhagyása akkor nem jelenti a mutatvány kudarcát, ha a hajítási parabola leszálló ága ismét simul a körhöz. Ebből következik, hogy a körpálya szimmetrikus darabjának kell hiányoznia és a parabola tetőpontjának a kör középpontja felett kell lennie. Ezt a feltételt úgy vehetjük legkönnyebben figyelembe, ha felírjuk, hogy az elmozdulás függőleges és vízszintes összetevői egyenlő idő alatt érkeznek el a kör középpontja felett levő maximumba. Az emelkedés ideje

t = v sin α / g

, a vízszintes elmozdulás ideje

t = R sin α / (v cos α)

. Ezeket egyenlővé téve:

\begin{matrix} \frac{v sin α}{g} = \frac{R sin α}{v cos α} . \end{matrix}

Ebből a feladat feltételének megfelelő

α

szög cos-ára ez az eredmény következik:

\begin{matrix} cos α = \frac{g R}{v^{2}} \end{matrix}

(4) felhasználásával:

\begin{matrix} cos α = \frac{g R}{[(k - 2) - 2 cos α] g R} . \end{matrix}

Ebből a feladat megoldása:

\begin{matrix} cos α = \frac{k - 2 \pm \sqrt[]{k^{2} - 4 k - 4}}{4} . \end{matrix}

Feladatunk számadataival

k = 5

α_{1} = 0^{\circ}

α_{2} = 60^{\circ}

.
A feladat taglalása a következő érdekességekre figyelmeztet. Az energiamegmaradás törvénye szerint arra a (függőlegestől mért)

β

szögre nézve, ameddig a tárgy a körön felmehet, ez következik:

\begin{matrix} \frac{m v^{2}}{2} = m g R (1 + cos β) . \end{matrix}

(4) figyelembevételével

cos β = \frac{k - 2}{2}

.
De idáig csak akkor futhat fel a tárgy, ha a pálya olyan, hogy a körön tartja. Arra a (függőlegestől mért)

γ

szögre nézve, amelynél a tárgy leesik a kör belsejéről, ez érvényes:

\begin{matrix} \frac{m v^{2}}{R} = m g cos γ . \end{matrix}

Ugyancsak (4) figyelembevételével:

\begin{matrix} cos γ = \frac{k - 2}{3} . \end{matrix}

β

kisebb, mint

γ

, tehát a tárgy a lehetséges legnagyobb magasság elérése előtt leesik. Táblázatunk néhány értéket tüntet fel ezekre a szögekre nézve.

\begin{matrix} k & γ & β & α \\ 2 & 90^{\circ} & 90^{\circ} \\ 3 & 70, 5^{\circ} & 60^{\circ} \\ 4 & 48^{\circ} & 0^{\circ} \\ 2 + 2 \sqrt[]{2} & 18, 5^{\circ} & 45^{\circ} 45^{\circ} \\ 4, 9 & 15^{\circ} & 18^{\circ} 56^{\circ} \\ 5 & 0^{\circ} & 0^{\circ} 60^{\circ} \\ 6 & 73^{\circ} \\ 7 & 77^{\circ} \end{matrix}

Az indítási sebességet

0

-tól kezdve növelve

k = 4

-ig a tárgy beesik a kör belsejébe, mielőtt az energiamegmaradás törvénye folytán lehetséges magasságot elérte volna.

k = 4

-nél már elérné a tárgy a kör tetejét, de előbb leesik.

k = 2 + 2 \sqrt[]{2}

-től kezdve lehet a tető egy darabját elhagyni.

k = 5

-ig

α

-ra két használható megoldásunk van; ebben az értéktartományban kétféleképp is elhagyható a körpálya teteje. Érdekes, ha nem vennénk le a tető egy darabját, akkor a mutatvány nem sikerülne, mert bizonyos

γ

szögnél a tárgy leesne a kör belsejébe.

k = 5

-től kezdődően a tárgy már képes volna leesés nélkül végigfutni a kör belsejében; a tető elhagyására ekkor már csak egy használható

α

szög kínálkozik.

2. Hőszigetelő falú edényben (7. ábra)

V_{1} = 3

liter térfogatú,

p_{1} = 4

atmoszféra nyomású és

T_{1} = 1092^{\circ}

K hőmérsékletű héliumgázt egy fal választ el

V_{2} = 2

liter térfogatú,

p_{2} = 2, 5

atmoszféra nyomású és

T_{2} = 1365^{\circ}

K hőmérsékletű héliumgáztól. A válaszfalat elengedjük, ezután a fal súrlódás nélkül mozoghat. Mekkora a nyomás az edényben, amikor a fal megáll, a) ha a mozgó fal jó hővezető, b) ha a mozgó fal tökéletesen hőszigetelő ?

(Bodó Zalán)

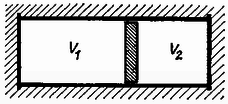7. ábra

Megoldás. Az edény merev, hőszigetelő fala azt jelenti, hogy a henger belsejében a gázmolekulák mozgási energiájának összege változatlan marad. Ennek a mozgási energiának a mértéke a

p

nyomás és

V

térfogat szorzata, amely egyébként

n R T

-vel egyenlő, ahol

n

a gáz móljainak száma,

T

a gáz abszolút hőmérséklete és

R

a gázállandó:

p V = n R T

. Kezdeti állapotban a gázmolekulák összes mozgási energiája

p_{1} V_{1} + p_{2} V_{2}

. A végső állapotban a nyomás a tartály mindegyik részében ugyanaz a

p

, a térfogatok

V_{I}

, és

V_{II}

. A végső állapotban a gázmolekulák összes mozgási energiája:

\begin{matrix} p V_{I} + p V_{II} = p (V_{I} + V_{II}) = p (V_{1} + V_{2}) . \end{matrix}

Ugyanis a gáz össztérfogata ugyanaz marad,

V_{I} + V_{II} = V_{1} + V_{2}

. Mivel a gázmolekulák összes mozgási energiája nem változhat meg:

\begin{matrix} p_{1} V_{1} + p_{2} V_{2} = p (V_{1} + V_{2}), \end{matrix}

innen az a közös nyomás, amely a fal megállásakor létrejön:

\begin{matrix} p = \frac{p_{1} V_{1} + p_{2} V_{2}}{V_{1} + V_{2}} \end{matrix}

Számadatainkkal

p = 3, 4

atmoszféra.
A végső egyensúly egyik feltétele a nyomások egyenlősége. Ehhez az a) esetben a hőmérséklet egyenlősége is járul. Mindegyik gáz-részre alkalmazzuk a gáztörvényt:

\begin{matrix} \frac{P_{1} V_{1}}{T_{1}} = \frac{p V_{I}}{T}, \frac{p_{2} V_{2}}{T_{2}} = \frac{p V_{II}}{T} . \end{matrix}

Ehhez járul a térfogatösszeg állandósága:

\begin{matrix} V_{I} + V_{II} = V_{1} + V_{2} . \end{matrix}

Így megvan a három egyenletünk

V_{I}

V_{II}

és

T

számára. A mi esetünkben

T_{1} = 4 \cdot 273^{\circ} K

T_{2} = 5 \cdot 273^{\circ} K

. Egyenletrendszerünk megoldása

T = 4, 25 \cdot 273^{\circ} K = 1160, 25^{\circ} K

V_{I} = 3, 75

liter,

V_{II} = 1, 25

liter.
A b) esetben, amikor a mozgó fal hőszigetelő, hiányzik a hőmérsékletek és térfogatok számára egy feltétel. A hőmérsékletek és térfogatok tekintetében a feladat határozatlan.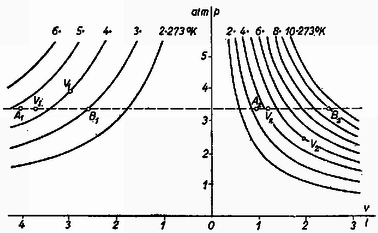

8. ábra

A 8. ábra jobb oldali része a tartály jobb oldali héliumgázának izotermáit tünteti fel. A bal oldalon, fordított irányban a bal oldali tartályrész gázának izotermái láthatók, figyelembe véve, hogy a bal oldali részben levő hélium normáltérfogata (tömege) a jobb oldalinak háromszorosa. A kezdeti állapotot

V_{1}

és

V_{2}

pontok tüntetik fel. A végső állapotot feltüntető pontoknak a

3, 4

atmoszféra magasságban húzódó vízszintesen kell feküdniök, de úgy, hogy abszcisszáik összege az 5 liter össztérfogatnak megfelelő távolság legyen. Az a) esetben, amikor a fal jó hővezetése folytán a hőmérsékletnek ki kell egyenlítődnie, a végső állapotot jelző

V_{I}

és

V_{II}

, pontok egyenlő hőmérsékletű izotermákon feküsznek. A b) esetben a két rész hőmérséklete az egyensúlyállapotban különböző lehet. Ekkor a végállapotot jelző két pont a

3, 4

atmoszféra magasságában húzott egyenesen, 5 liternek megfelelő távolságban akárhol helyezkedhet el, különböző hőmérsékletű izotermákon is. Például lehetséges végállapot

A_{1}

és

A_{2}

(4 liter,

4, 533 \cdot 273^{\circ} K

és 1 liter,

3, 4 \cdot 273^{\circ} K

), azután

B_{1}

és

B_{2}

pont

(2, 5

liter,

2, 833 \cdot 273^{\circ} K

és

2, 5

liter,

8, 5 \cdot 273^{\circ} K

) stb. Hőszigetelő fal esetében vezetéssel nem tudják az egyik gázrész molekulái kinetikus energiájuk egy részét a másik gázrésznek átadni. Ellenben az egyes gázrészek molekuláinak mozgási energiája mégis megváltozik annak következtében, hogy a mozgó fal megüti és felgyorsítja azokat. Mindkét esetben az elinduló fal lengéseket végez, amelyeket a gáz belső súrlódása lefékez, megállít. (Az ideális gáznak is van belső súrlódása, mert ez a molekulák véges méretének következménye. A véges méret teszi lehetővé a molekulák kölcsönös ütközését és ezzel a sebességeloszlás egyensúlyának létrejöttét.)

3. Három gyűjtőlencsénk van. Fókusztávolságaik

90 cm

10 cm

és

8 cm

. Hogyan kell ezekből a lehető legnagyobb nagyítású távcsövet összeállítani, ha a távcső hossza legfeljebb

150 cm

lehet ? (A lencsék vékonyak és minden lencsehibától eltekintünk.)

(Bodó Zalán)

Megoldás. Úgynevezett földi messzelátót készítünk (9. ábra).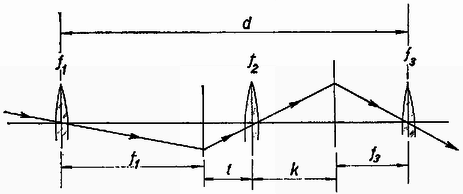

9. ábra

f_{1}

tárgylencse-fókusztávolságban keletkezik az első kép. A második kép a szemlencse előtt, ettől

f_{3}

fókusztávolságban keletkezik. Tehát a

d

távcsőhosszból a fordítólencse

t + k

-jára

d - f_{1} - f_{3}

marad:

\begin{matrix} t + k = d - f_{1} - f_{3} \end{matrix}

A lencsetörvény a fordítólencsére nézve:

\begin{matrix} \frac{1}{t} + \frac{1}{k} = \frac{1}{f_{2}} . \end{matrix}

Az egyenletrendszer megoldása:

\begin{matrix} t = \frac{d - f_{1} - f_{3} - \sqrt[]{(d - f_{1} - f_{3}) (d - f_{1} - f_{3} - 4 f_{2})}}{2}, \\ k = \frac{d - f_{1} - f_{3} + \sqrt[]{(d - f_{1} - f_{3}) (d - f_{1} - f_{3} - 4 f_{2})}}{2} . \end{matrix}

A tárgylencse szögnagyítása

f_{1} / t

, a szemlencse szögnagyítása

k / f_{3}

, a teljes szögnagyítás:

\begin{matrix} N = \frac{f_{1}}{t} \cdot \frac{k}{f_{3}} = \frac{f_{1}}{f_{3}} \cdot \frac{k}{t} . \end{matrix}

k

és

t

előbbi értékeit felhasználva:

\begin{matrix} N = \frac{f_{1}}{f_{3}} \cdot \frac{1 + \sqrt[]{1 - 4 f_{2} / (d - f_{1} - f_{3})}}{1 - \sqrt[]{1 - 4 f_{2} / (d - f_{1} - f_{3})}} . \end{matrix}

Különböző összeállításokat próbálunk ki. Nyilván az

f_{1} = 90 cm

gyújtótávolságú lencse lesz a tárgylencse és felhasználjuk a teljes

d = 150 cm

hosszúságot. Az alábbi eredményeket nyerjük:

\begin{matrix} \begin{matrix} f_{1} & f_{2} & f_{3} & t \end{matrix} \end{matrix}

Látható, hogy a legjobb nagyítást akkor kapjuk, ha a fordító lencse a 8 cm-es, a szemlencse a 10 cm-es gyújtótávolságú. Megvizsgálhatjuk, hogy két lencsét lencserendszerré egyesítve az ezzel összeállított csillagászati távcső nagyítása bármely kombinációban kisebb, mint 36.

Az 1970. évi fizika tanulmányi verseny eredménye

I. díj Göndöcs Ferenc (Győr, Révai M. g. III. o. t. Tanára: Takács István).
II. díj Kereszturi András (Budapest, Eötvös J. g. IV. o. t. Tanára: Kellner Dénes).
III. díj Borzsák Péter (Budapest, I. István g. IV. o. t. Tanára: Cseh Géza).

A további helyezettek: 4. Bajmóczy Ervin (Budapest, Fazekas M. g. III. o. t.), 5. Mosó Tamás (Budapest, Eötvös J. g. III. o. t.), 6. Lempert László (Budapest, Radnóti M. g. IV. o. t.), 7. Horváthy Péter (Budapest, Fazekas M. g. IV. o. t.), 8. Dávid Gyula (Budapest, József A. g. III o. t.), 9. Láz József (Budapest, Eötvös J. g. IV. o. t.), 10. Faragó Tamás (Debrecen, KLTE gyakorló g. III. o. t.).